cho trước một số điểm trong đó có 3 điểm nào thẳng hàng vẽ các đường thẳng đi qua các điểm biết tổng số đường thẳng là 120 Hỏi có bao nhiêu có bao nhiêu điểm cho trước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


27.75 + 25.27 - 150
= 27.(75 + 25) - 150
= 27.100 - 150
= 2700 - 150
= 2550
b; 142 - [50 - (23 x 10 - 23.5)]
= 142 - [50 - 23x (10 - 5)]
= 142 - [50 - 23 x 5]
= 142 - [50 - 115]
= 142 - [ - 65]
= 142 + 65
= 207

\(F=\dfrac{\dfrac{2010}{1}+\dfrac{2009}{2}+...+\dfrac{1}{2010}+2010}{1+\dfrac{1}{2}+...+\dfrac{1}{2010}}\)
\(=\dfrac{\left(\dfrac{2010}{1}+1\right)+\left(\dfrac{2009}{2}+1\right)+...+\left(\dfrac{1}{2010}+1\right)}{1+\dfrac{1}{2}+...+\dfrac{1}{2010}}\)
\(=\dfrac{\dfrac{2011}{1}+\dfrac{2011}{2}+...+\dfrac{2011}{2010}}{1+\dfrac{1}{2}+...+\dfrac{1}{2010}}=2011\)

a: 15:(x+2)=3
=>\(x+2=\dfrac{15}{3}=5\)
=>x=5-2=3
b: 20(1+x)=2
=>\(x+1=\dfrac{2}{20}=\dfrac{1}{10}\)
=>\(x=\dfrac{1}{10}-1=-\dfrac{9}{10}\)
f: \(12x-33=3^2\cdot3^3\)
=>\(12x-33=3^5=243\)
=>12x=243+33=276
=>\(x=\dfrac{276}{12}=23\)
g: 541+(218-x)=73
=>218-x=73-541=-468
=>x=218+468=686

a) Ta có:
\(\left(x-5\right)⋮\left(x+1\right)\\ \Rightarrow\left(x+1-6\right)⋮\left(x+1\right)\\ \Rightarrow-6⋮\left(x+1\right)\\ \Rightarrow\left(x+1\right)\inƯ\left(-6\right)=\left\{\pm1,\pm2,\pm3,\pm6\right\}\)
\(\Rightarrow x\in\left\{0,-2,1,-3,2,-4,5,-7\right\}\) (thỏa mãn điều kiện x nguyên)
Vậy...
b) Ta có:
\(\left(x+2\right)⋮\left(x-3\right)\\ \Rightarrow\left(x-3+5\right)⋮\left(x-3\right)\\ \Rightarrow5⋮\left(x-3\right)\\ \Rightarrow\left(x-3\right)\inƯ\left(5\right)=\left\{\pm1,\pm5\right\}\)
\(\Rightarrow x\in\left\{4,2,8,-2\right\}\) (thỏa mãn điều kiện x nguyên)
Vậy...
a) Do `x` là số nguyên
`=> x - 5 ` và `x + 1` là các số nguyên
Ta có: `x-5 ⋮ x+1`
`=> (x+1) - 6 ⋮ x+1`
Do `x + 1 ⋮ x+1`
`=> 6 ⋮ x+1`
`=> x + 1` thuộc `Ư(6) =` {`-6;-3;-2;-1;1;2;3;6`}
`=> x` thuộc {`-7;-4;-3;-2;0;1;2;5`} (Thỏa mãn)
b) Do `x` là số nguyên
`=> x +2` và `x -3` là các số nguyên
Ta có: `x+2 ⋮ x-3`
`=> (x-3) + 5 ⋮ x-3`
Do `x-3 ⋮ x-3`
`=> 5 ⋮ x-3`
`=> x -3` thuộc `Ư(5) =` {`-5;-1;1;5`}
`=> x` thuộc {`-2;2;4;8`} (Thỏa mãn)

Thời gian xe thứ nhất đi từ A đến chỗ gặp là:
\(8h30p-6h25p=2h5p=\dfrac{25}{12}\left(giờ\right)\)
Thời gian xe thứ hai đi từ A đến chỗ gặp là:
\(8h30p-7h40p=50p=\dfrac{5}{6}\left(giờ\right)\)
Vận tốc của xe thứ nhất là:
\(12\times\dfrac{5}{6}:\left(\dfrac{25}{12}-\dfrac{5}{6}\right)=10:\dfrac{15}{12}=10\times\dfrac{4}{5}=8\left(\dfrac{km}{h}\right)\)
Vận tốc của xe thứ hai là 8+12=20(km/h)

Hiệu số phần bằng nhau là 4-1=3(phần)
Tuổi Huy năm nay là 27:3x1=9(tuổi)
Năm sinh của Huy là 2024-9=2015
Do mẹ sinh ra Huy lúc mẹ Huy `27` tuổi nên hiệu số tuổi của mẹ và Huy là `27` tuổi
Ta có sơ đồ:
Tuổi Huy 2024: (1 phần)
Tuổi mẹ 2024: (4 phần)
Hiệu số phần bằng nhau là: `4 - 1 = 3` (phần)
Giá trị 1 phần là: `27 : 3 = 9` (tuổi)
Tuổi Huy năm 2024 là: `9` x `1 = 9` (tuổi)
Thời điểm Huy sinh ra là vào năm: `2024 - 9 - 2015`
Vậy Huy sinh ra vào năm `2015`

Bài 3:
\(a.\dfrac{5}{3}+\left(7+\dfrac{-5}{3}\right)\\ =\dfrac{5}{3}+7+\dfrac{-5}{3}\\ =\left(\dfrac{5}{3}-\dfrac{5}{3}\right)+7\\ =7\\ b.\dfrac{-7}{31}+\left(\dfrac{24}{17}+\dfrac{7}{31}\right)\\ =\dfrac{-7}{31}+\dfrac{24}{17}+\dfrac{7}{31}\\ =\left(\dfrac{7}{31}-\dfrac{7}{31}\right)+\dfrac{24}{17}\\ =\dfrac{24}{17}\\ c.\dfrac{3}{7}+\left(\dfrac{-1}{5}+\dfrac{-3}{7}\right)\\ =\dfrac{3}{7}+\dfrac{-1}{5}+\dfrac{-3}{7}\\ =\left(\dfrac{3}{7}-\dfrac{3}{7}\right)+\dfrac{-1}{5}\\ =-\dfrac{1}{5}\)
Bài 2:
a: \(\dfrac{2}{7}+\dfrac{3}{7}=\dfrac{2+3}{7}=\dfrac{5}{7}\)
b: \(\dfrac{3}{8}+\dfrac{5}{8}=\dfrac{3+5}{8}=\dfrac{8}{8}=1\)
c: \(\dfrac{1}{7}+\dfrac{-4}{7}=\dfrac{1-4}{7}=-\dfrac{3}{7}\)
d: \(\dfrac{7}{-25}+\dfrac{-8}{25}=\dfrac{-7}{25}+\dfrac{-8}{25}=-\dfrac{15}{25}=-\dfrac{3}{5}\)
e: \(\dfrac{6}{18}+\dfrac{-14}{21}=\dfrac{1}{3}-\dfrac{2}{3}=-\dfrac{1}{3}\)
f: \(\dfrac{6}{13}+\dfrac{-14}{39}=\dfrac{18}{39}-\dfrac{14}{39}=\dfrac{4}{39}\)
g: \(-\dfrac{3}{21}+\dfrac{6}{42}=-\dfrac{3}{21}+\dfrac{3}{21}=0\)
h: \(\dfrac{7}{21}+\dfrac{9}{-36}=\dfrac{1}{3}-\dfrac{1}{4}=\dfrac{1}{12}\)
Bài 4:
a: \(\dfrac{6}{5}+\left(3+\dfrac{-1}{5}\right)\)
\(=\dfrac{6}{5}+3-\dfrac{1}{5}\)
=1+3=4
b: \(-\dfrac{3}{5}+\left(-\dfrac{2}{5}+2\right)\)
\(=-\dfrac{3}{5}-\dfrac{2}{5}+2=2-1=1\)
c: \(-\dfrac{3}{5}+\left(-\dfrac{2}{5}+2\right)\)
\(=-\dfrac{3}{5}-\dfrac{2}{5}+2\)
=2-1=1
d: \(-\dfrac{5}{11}+\left(-\dfrac{6}{11}+1\right)\)
\(=-\dfrac{5}{11}-\dfrac{6}{11}+1=1-1=0\)
e: \(-\dfrac{17}{13}+\left(\dfrac{25}{101}+\dfrac{4}{13}\right)\)
\(=-\dfrac{17}{13}+\dfrac{4}{13}+\dfrac{25}{101}\)
\(=-1+\dfrac{25}{101}=-\dfrac{76}{101}\)


150 số chẵn đầu tiên là 0;2;4;...;298
Tổng của 150 số chẵn đầu tiên là:
(0+298)x150:2=22350
Giải:
Số chẵn đầu tiên là: 0
Khoảng cách giữa các số chẵn liên tiếp là: 2 - 0 = 2
Số chẵn thứ 150 là: 2 x (150 - 1) + 0 = 298
Tổng của 150 số chẵn đầu tiên là: (298 + 0) x 150 : 2 = 22350
Đáp số: 22350
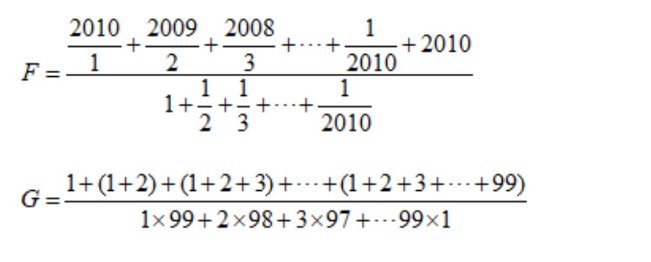 Gíup mình nha
Gíup mình nha
Gọi số điểm cho trước là x(điểm)
(Điều kiện: \(x\in Z^+;x>3\))
Số điểm không thẳng hàng là x-3(điểm)
TH1: vẽ 1 đường thẳng đi qua 3 điểm thẳng hàng
=>Có 1 đường thẳng
TH2: Chọn 2 điểm bất kì trong x-3 điểm còn lại
Số đường thẳng là \(C^2_{x-3}=\dfrac{\left(x-3\right)!}{\left(x-3-2\right)!\cdot2!}=\dfrac{\left(x-4\right)\left(x-3\right)}{2}\)(đường)
TH3: Chọn 1 điểm trong 3 điểm thẳng hàng, 1 điểm trong x-3 điểm còn lại
=>Có 3(x-3) đường thẳng
Tổng số đường thẳng là 120 đường nên ta có:
\(1+\dfrac{\left(x-4\right)\left(x-3\right)}{2}+3\left(x-3\right)=120\)
=>\(\dfrac{2+\left(x-4\right)\left(x-3\right)+6\left(x-3\right)}{2}=120\)
=>2+(x-4)(x-3)+6(x-3)=240
=>\(2+x^2-7x+12+6x-18=240\)
=>\(x^2-x-244=0\)
=>\(\left[{}\begin{matrix}x=\dfrac{1+\sqrt{977}}{2}\left(loại\right)\\x=\dfrac{1-\sqrt{977}}{2}\left(loại\right)\end{matrix}\right.\)