a: \(\dfrac{15}{21}=\dfrac{x}{-7}\)

=>\(\dfrac{x}{-7}=\dfrac{5}{7}\)

=>\(x=-5\)

b: \(\dfrac{5}{x}=\dfrac{15}{-20}\)

=>\(x=\dfrac{5\cdot\left(-20\right)}{15}=\dfrac{-100}{15}=-\dfrac{20}{3}\)

c: \(\dfrac{5}{3}=\dfrac{x}{9}\)

=>\(x=5\cdot\dfrac{9}{3}=5\cdot3=15\)

d: \(3x-\dfrac{7}{8}=\dfrac{5}{2}\)

=>\(3x=\dfrac{5}{2}+\dfrac{7}{8}=\dfrac{20+7}{8}=\dfrac{27}{8}\)

=>\(x=\dfrac{27}{8}:3=\dfrac{9}{8}\)

\(\dfrac{6}{5}x=\dfrac{9}{2}y=\dfrac{18}{7}z\)

=>\(\dfrac{x}{\dfrac{5}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{7}{18}}\)

Đặt \(\dfrac{x}{\dfrac{5}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{7}{18}}=k\)

=>\(x=\dfrac{5}{6}k;y=\dfrac{2}{9}k;z=\dfrac{7}{18}k\)

\(2x^2+3y^2-z^2=4\)

=>\(2\cdot\left(\dfrac{5}{6}k\right)^2+3\cdot\left(\dfrac{2}{9}k\right)^2-\left(\dfrac{7}{18}k\right)^2=4\)

=>\(\dfrac{50}{36}k^2+\dfrac{4}{27}k^2-\dfrac{49}{324}k^2=4\)

=>\(k^2=\dfrac{1296}{449}\)

=>\(k=\pm\dfrac{36}{\sqrt{449}}\)

TH1: \(k=\dfrac{36}{\sqrt{449}}\)

=>\(x=\dfrac{5}{6}\cdot\dfrac{36}{\sqrt{449}}=\dfrac{30}{\sqrt{449}};y=\dfrac{2}{9}\cdot\dfrac{36}{\sqrt{449}}=\dfrac{8}{\sqrt{449}};z=\dfrac{7}{18}\cdot\dfrac{36}{\sqrt{449}}=\dfrac{14}{\sqrt{449}}\)

TH2: \(k=-\dfrac{36}{\sqrt{449}}\)

=>\(x=\dfrac{5}{6}\cdot\dfrac{-36}{\sqrt{449}}=\dfrac{-30}{\sqrt{449}};y=\dfrac{2}{9}\cdot\dfrac{-36}{\sqrt{449}}=\dfrac{-8}{\sqrt{449}};z=\dfrac{7}{18}\cdot\dfrac{-36}{\sqrt{449}}=\dfrac{-14}{\sqrt{449}}\)

\(\dfrac{x}{y}=\dfrac{5}{3}\)

=>\(\dfrac{x}{5}=\dfrac{y}{3}\)

mà x+2y=4,4

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{x+2y}{5+2\cdot3}=\dfrac{4.4}{11}=0,4\)

=>\(x=0,4\cdot5=2;y=0,4\cdot3=1,2\)

`#3107.101107`

\(\dfrac{x}{y}=\dfrac{5}{3}\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}\Rightarrow\dfrac{x}{5}=\dfrac{2y}{6}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{5}=\dfrac{2y}{6}=\dfrac{x+2y}{5+6}=\dfrac{4,4}{11}=0,4\)

\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}=0,4\)

\(\Rightarrow x=0,4\cdot5=2\) `;` \(y=0,4\cdot3=1,2\)

Vậy, `x = 2; y = 1,2.`

2x=3y

=>\(\dfrac{x}{3}=\dfrac{y}{2}\)

=>\(\dfrac{x}{21}=\dfrac{y}{14}\left(1\right)\)

5y=7z

=>\(\dfrac{y}{7}=\dfrac{z}{5}\)

=>\(\dfrac{y}{14}=\dfrac{z}{10}\left(2\right)\)

Từ (1) và (2) suy ra \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\)

Đặt \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}=k\)

=>x=21k; y=14k; z=10k

3x-2y+5z=-30

=>\(3\cdot21k-2\cdot14k+5\cdot10k=-30\)

=>85k=-30

=>\(k=-\dfrac{30}{85}=-\dfrac{6}{17}\)

=>\(x=21\cdot\dfrac{-6}{17}=\dfrac{-126}{17};y=14\cdot\dfrac{-6}{17}=-\dfrac{84}{17};z=10\cdot\dfrac{-6}{17}=-\dfrac{60}{17}\)

\(2x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}\)

\(5y=7z\Rightarrow\dfrac{y}{7}=\dfrac{z}{5}\Rightarrow\dfrac{y}{14}=\dfrac{z}{10}\)

\(\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\)

Áp dụng t/c dãy tỉ số bằng nhau:

\(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}=\dfrac{3x}{63}=\dfrac{2y}{28}=\dfrac{5z}{50}=\dfrac{3x-2y+5z}{63-28+50}=\dfrac{-30}{85}\)

\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{30}{85}.21=-\dfrac{126}{17}\\y=-\dfrac{30}{85}.14=-\dfrac{84}{17}\\z=-\dfrac{30}{85}.10=-\dfrac{60}{17}\end{matrix}\right.\)

Em có ghi nhầm đề đâu ko mà kết quả xấu quá

Yêu cầu đề bài là gì vậy bạn?

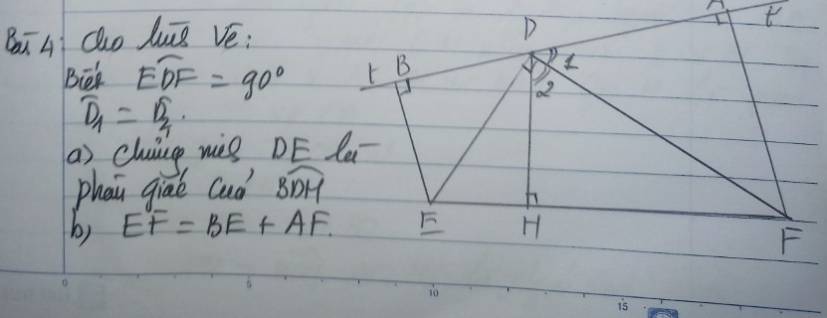
a.

Ta có: \(\widehat{BDE}+\widehat{EDF}+\widehat{D_1}=180^0\)

\(\Rightarrow\widehat{BDE}+90^0+\widehat{D_1}=180^0\)

\(\Rightarrow\widehat{BDE}+\widehat{D_1}=90^0\)

Mà \(\widehat{D_1}=\widehat{D_2}\Rightarrow\widehat{BDE}+\widehat{D_2}=90^0\)

Lại có \(\widehat{HDE}+\widehat{D_2}=\widehat{EDF}=90^0\)

\(\Rightarrow\widehat{BDE}=\widehat{HDE}\)

\(\Rightarrow DE\) là phân giác của \(\widehat{BDH}\)

b.

Xét hai tam giác vuông BDE và HDE có:

\(\left\{{}\begin{matrix}DE-chung\\\widehat{BDE}=\widehat{HDE}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta_{\perp}BDE=\Delta_{\perp}HDE\left(ch-gn\right)\)

\(\Rightarrow BE=HE\)

Tương tự, xét 2 tam giác vuông HDF và ADF có:

\(\left\{{}\begin{matrix}DF-chung\\\widehat{D_2}=\widehat{D_1}\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\Delta_{\perp}HDF=\Delta_{\perp}ADF\left(ch-gn\right)\)

\(\Rightarrow AF=HF\)

\(\Rightarrow HE+HF=BE+AF\)

\(\Rightarrow EF=BE+AF\)

cứu với

Theo cm câu b, do \(\Delta BEG=\Delta BFH\Rightarrow EG=FH\) và \(\widehat{BGE}=\widehat{BHF}\)

Hay \(\widehat{IGE}=\widehat{KHF}\)

Do EI vuông góc BG nên tam giác EIG vuông tại I

Do FK vuông góc BH nên tam giác FKH vuông tại K

Xét hai tam giác vuông EIG và FKH có:

\(\left\{{}\begin{matrix}EG=FH\left(cmt\right)\\\widehat{IGE}=\widehat{KHF}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta_{\perp}EIG=\Delta_{\perp}FKH\left(ch-gn\right)\)

\(\Rightarrow EI=FK\)

a: Xét ΔBEF có

BA là đường cao

BA là đường trung tuyến

Do đó: ΔBEF cân tại B

=>BE=BF

b: Xét ΔBGH có

BA là đường cao

BA là đường trung tuyến

Do đó: ΔBGH cân tại B

=>BG=BH

Ta có: AF+FH=AH

AE+EG=AG

mà AF=AE và AH=AG

nên FH=EG

Xét ΔBFH và ΔBEG có

BF=BE

FH=EG

BH=BG

Do đó: ΔBFH=ΔBEG

c: Xét ΔKHF vuông tại K và ΔIGE vuông tại I có

FH=EG

\(\widehat{H}=\widehat{G}\)(ΔBHG cân tại B)

Do đó: ΔKHF=ΔIGE

=>FK=EI