
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a) \(\dfrac{-7}{-13}=\dfrac{7}{13}\) là số hưu tỉ dương
b) \(\dfrac{2}{-17}=-\dfrac{2}{17}\) là số hưu tỉ âm
c) \(-\dfrac{-6}{5}=\dfrac{6}{5}\) là số hưu tỉ dương
Bài 3:
a) \(-2\dfrac{1}{4}=-\left(2+\dfrac{1}{4}\right)=-\dfrac{9}{4}\)
b) \(6\dfrac{2}{3}=6+\dfrac{2}{3}=\dfrac{20}{3}\)
c) \(-3\dfrac{1}{4}=-\left(3+\dfrac{1}{4}\right)=-\dfrac{13}{4}\)

a: \(x^2+y^2>=2xy\)
=>\(x^2-2xy+y^2>=0\)
=>\(\left(x-y\right)^2>=0\)(luôn đúng)
b: \(x^2+4xy>=-4y^2\)
=>\(x^2+4xy+4y^2>=0\)
=>\(\left(x+2y\right)^2>=0\)(luôn đúng)
c: \(2\left(x^2+y^2\right)>=\left(x+y\right)^2\)
=>\(2x^2+2y^2-x^2-2xy-y^2>=0\)
=>\(x^2-2xy+y^2>=0\)
=>\(\left(x-y\right)^2>=0\)(luôn đúng)

d: A={11;12;13;14;15;16;17;18;19;20}
A={x\(\in\)N|11<=x<=20}
Số phần tử của tập hợp A là 20-11+1=20-10=10(phần tử)
e: D={10;11;12;13;14;15}
D={x\(\in\)N|9<x<=15}
D có 15-10+1=5+1=6 phần tử
f: F={1;2;3;...;30}
F={x\(\in Z^+\)|x<=30}
Số phần tử của tập hợp F là 30-1+1=30(phần tử)
g: G={x\(\in\)N|x>5}
G={6;7;8;...}
G có vô số phần tử
h: C={18;19;...;100}
C={x\(\in\)N|18<=x<=100}
Số phần tử của tập hợp C là 100-18+1=83(phần tử)
i: B={102;105;...;999}
B={x\(\in\)N|100<=x<=999;x\(⋮\)3}
Số phần tử của tập hợp B là \(\left(999-102\right):3+1=300\)(phần tử)

a: 2a+3>2b+3
=>2a>2b
=>a>b
b: -3a-1>=-3b-1
=>\(-3a>=-3b\)
=>3a<=3b
=>a<=b
c: 5-2a<5-a-b
=>5-2a+a<5-b
=>5-a<5-b
=>a-5>b-5
=>a>b

a: 2<3
=>\(2+8,5\cdot6< 3+8,5\cdot6\)
b: 2<3
=>\(\sqrt{2}< \sqrt{3}\)
=>\(-\sqrt{2}>-\sqrt{3}\)
=>\(30-\sqrt{2}>30-\sqrt{3}\)
c:
Vì 3>2
nên \(3\sqrt{3}>3\sqrt{2}\)
=>\(-3\sqrt{3}< -3\sqrt{2}\)
mà 35<36
nên \(35-3\sqrt{3}< 36-3\sqrt{2}\)

13: \(x^3-6x^2+12x-8\)
\(=x^3-3\cdot x^2\cdot2+3\cdot x\cdot2^2-2^3\)
\(=\left(x-2\right)^3\)
14: \(8x^3+12x^2y+6xy^2+y^3\)
\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2+y^3\)
\(=\left(2x+y\right)^3\)
16: \(x^{10}-1=\left(x^5-1\right)\left(x^5+1\right)=\left(x-1\right)\left(x^4+x^3+x^2+x+1\right)\left(x+1\right)\left(x^4-x^3+x^2-x+1\right)\)
17: \(x^2-9=x^2-3^2=\left(x-3\right)\left(x+3\right)\)
18: \(4x^2-25=\left(2x\right)^2-5^2=\left(2x-5\right)\left(2x+5\right)\)
19: \(x^4-y^4=\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
20: \(9x^2+6xy+y^2=\left(3x\right)^2+2\cdot3x\cdot y+y^2=\left(3x+y\right)^2\)
21: \(6x-9-x^2=-\left(x^2-6x+9\right)\)
\(=-\left(x^2-2\cdot x\cdot3+3^2\right)\)
\(=-\left(x-3\right)^2\)
22: \(x^2+4xy+4y^2=x^2+2\cdot x\cdot2y+\left(2y\right)^2=\left(x+2y\right)^2\)
23: \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=\left(x+y-x+y\right)\left(x+y+x-y\right)\)
\(=2x\cdot2y=4xy\)
24: \(\left(x+y+z\right)^2-4z^2\)
\(=\left(x+y+z\right)^2-\left(2z\right)^2\)
\(=\left(x+y+z-2z\right)\left(x+y+z+2z\right)\)
\(=\left(x+y-z\right)\left(x+y+3z\right)\)
25: \(\left(3x+1\right)^2-\left(x+1\right)^2\)
\(=\left(3x+1-x-1\right)\left(3x+1+x+1\right)\)
\(=2x\left(4x+2\right)=4x\left(2x+1\right)\)
26: \(x^3y^3+125=\left(xy\right)^3+5^3\)
\(=\left(xy+5\right)\left(x^2y^2-5xy+25\right)\)
27: \(8x^3-y^3-6xy\left(2x-y\right)\)
\(=\left(2x-y\right)\left(4x^2+2xy+y^2\right)-6xy\left(2x-y\right)\)
\(=\left(2x-y\right)\left(4x^2+2xy+y^2-6xy\right)\)
\(=\left(2x-y\right)\left(4x^2-4xy+y^2\right)=\left(2x-y\right)^3\)
28: \(\left(3x+2\right)^2-2\left(x-1\right)\left(3x+2\right)+\left(x-1\right)^2\)
\(=\left(3x+2-x+1\right)^2\)
\(=\left(2x+3\right)^2\)

Bài 4:
a: 4x-y=1
=>y=4x-1
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=4x-1\end{matrix}\right.\)
b: x+3y=-2
=>x=-3y-2
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}y\in R\\x=-3y-2\end{matrix}\right.\)
Bài 5:
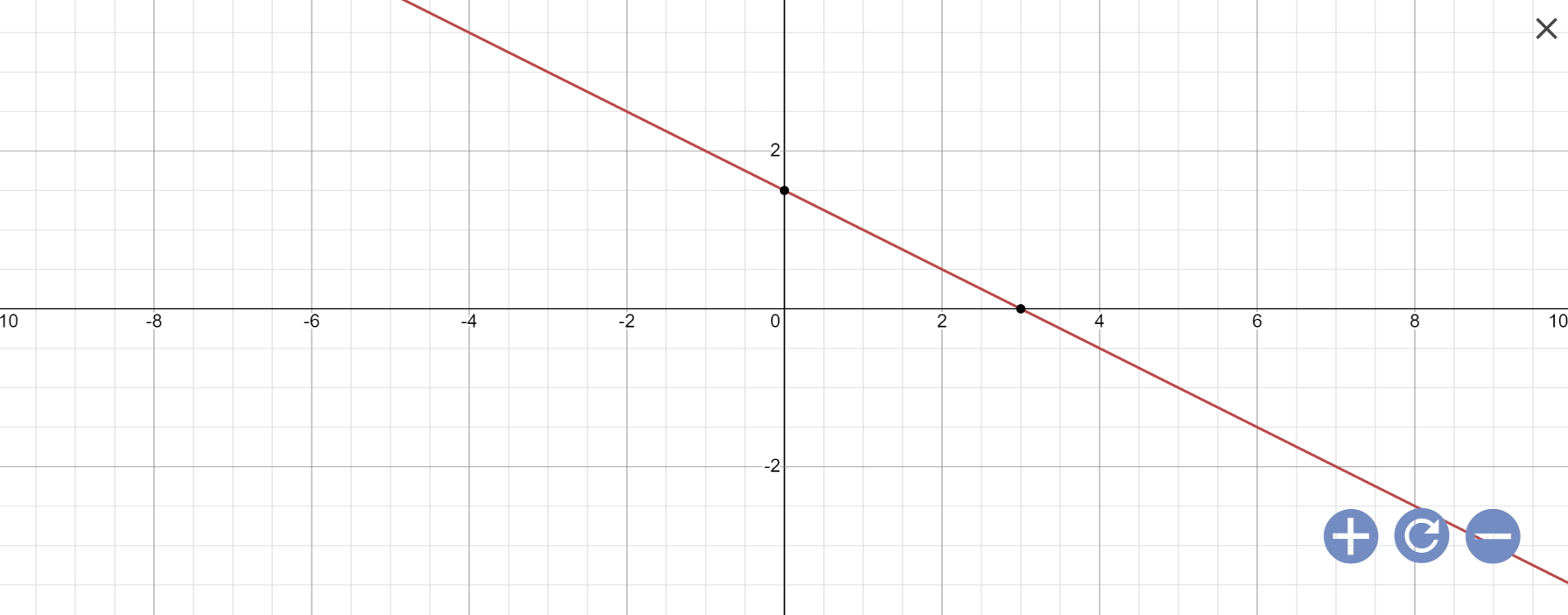
x+2y-3=0
=>2y=-x+3
=>\(y=\dfrac{-x+3}{2}\)
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{-x+3}{2}\end{matrix}\right.\)
Biểu diễn tập nghiệm:

Bài 1:
\(3^{39}< 3^{40}=\left(3^4\right)^{10}=81^{10}\)
\(11^{21}>11^{20}=121^{10}\)
mà 121>81
nên \(11^{21}>3^{39}\)
Bài 2:
\(5^{27}=\left(5^3\right)^9=125^9;2^{63}=\left(2^7\right)^9=128^9\)
mà 125<128
nên \(5^{27}< 2^{63}\)
\(2^{63}=\left(2^9\right)^7=512^7;5^{28}=\left(5^4\right)^7=625^7\)
mà 512<625
nên \(2^{63}< 5^{28}\)
Do đó: \(5^{27}< 2^{63}< 5^{28}\)


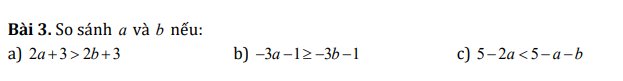
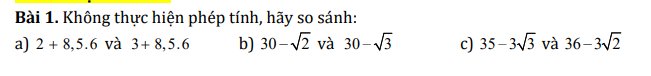

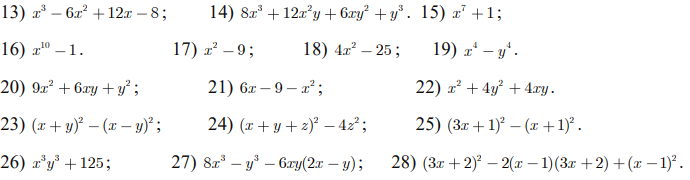


a: \(\dfrac{x}{y}+\dfrac{y}{x}>=2\cdot\sqrt{\dfrac{x}{y}\cdot\dfrac{y}{x}}=2\)
b: \(\dfrac{1}{x}+\dfrac{1}{y}>=\dfrac{4}{x+y}\)
=>\(\dfrac{x+y}{xy}>=\dfrac{4}{x+y}\)
=>\(\left(x+y\right)^2>=4xy\)
=>\(x^2+2xy+y^2-4xy>=0\)
=>\(x^2-2xy+y^2>=0\)
=>\(\left(x-y\right)^2>=0\)(luôn đúng)