Áp dụng BĐT Cô-si cho 3 số dương \(x^2,y^2,z^2\) , ta có:\(x^2+y^2+z^2\ge3\sqrt[3]{\left(xyz\right)^2}\)

\(\Leftrightarrow\left(xyz\right)^2\le\dfrac{\left(x^2+y^2+z^2\right)^3}{27}\) \(=\dfrac{1}{27}\)

\(\Leftrightarrow-\dfrac{1}{3\sqrt{3}}\le xyz\le\dfrac{1}{3\sqrt{3}}\)

 Vậy \(max_{xyz}=\dfrac{1}{3\sqrt{3}}\). Dấu "=" xảy ra khi \(x^2=y^2=z^2\) 

\(\Rightarrow\left(x,y,z\right)=\left(\dfrac{1}{\sqrt{3}},\dfrac{1}{\sqrt{3}},\dfrac{1}{\sqrt{3}}\right)\) hoặc \(\left(\dfrac{1}{\sqrt{3}},-\dfrac{1}{\sqrt{3}},-\dfrac{1}{\sqrt{3}}\right)\) và các hoán vị.

\(a)\left(x^2+2x\right)\left(x^2+2x+4\right)+3\)

Để đơn giản hơn cũng như là dễ nhìn hơn thì ta :

Đặt : \(x^2+2x=a\)

Do đó ta có đa thức :

\(a.\left(a+4\right)+3=a^2+4a+3\)

\(=a^2+a+3a+3\)

\(=a\left(a+1\right)+3\left(a+1\right)\)

\(=\left(a+1\right)\left(a+3\right)\)

\(=\left(x^2+2x+1\right)\left(x^2+2x+3\right)\)

\(=\left(x+1\right)^2.\left(x^2+2x+3\right)\)

Hoặc bạn có thể đặt \(x^2+2x+2=t\)

Thì \(P=\left(x^2+2x\right)\left(x^2+2x+4\right)+3\)

\(P=\left(t-2\right)\left(t+2\right)+3\)

\(P=t^2-4+3\)

\(P=t^2-1\)

\(P=\left(t-1\right)\left(t+1\right)\)

\(P=\left(x^2+2x+1\right)\left(x^2+2x+3\right)\)

\(P=\left(x+1\right)^2\left(x^2+2x+3\right)\)

\(\text{#3107}\)

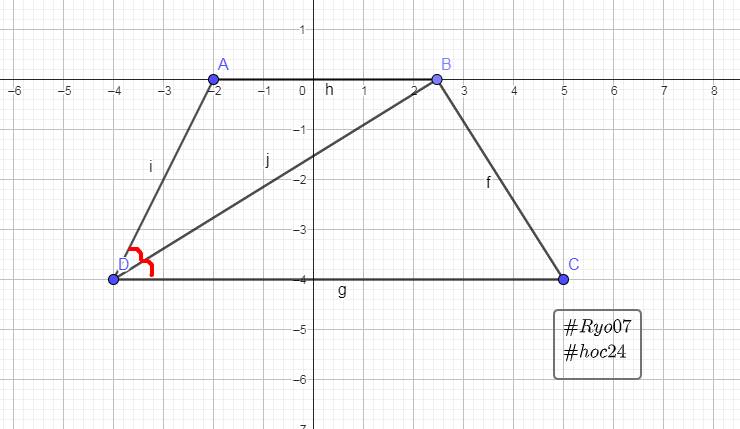
a)

Vì BD là tia phân giác của \(\widehat{\text{ADC}}\)

\(\Rightarrow\widehat{\text{ADB}}=\widehat{\text{CDB}}=\dfrac{1}{2}\widehat{\text{ADC}}\)

Mà ABCD là hình thang cân

\(\Rightarrow\widehat{\text{C}}=\widehat{\text{D}}\)

\(\Rightarrow\widehat{\text{C}}=2\widehat{\text{BDC}}\)

Xét `\Delta BDC:`

\(\widehat{\text{BDC}}+\widehat{\text{CBD}}+\widehat{\text{C}}=180^0\\ \Rightarrow\widehat{\text{BDC}}+90^0+2\widehat{\text{BDC}}=180^0\\ \Rightarrow3\widehat{\text{BDC}}=90^0\\ \Rightarrow\widehat{\text{BDC}}=30^0\)

Vì \(\widehat{\text{C}}=2\widehat{\text{BDC}}\)

\(\Rightarrow\widehat{\text{C}}=2\cdot30^0\\ \Rightarrow\widehat{\text{C}}=60^0\)

Vì $\widehat{C} = \widehat{D}$

\(\Rightarrow\widehat{\text{C}}=\widehat{\text{D}}=60^0\)

Vì ABCD là hình thang cân

\(\Rightarrow\widehat{\text{A}}+\widehat{\text{D}}=180^0\left(\text{2 góc trong cùng phía bù nhau}\right)\\ \Rightarrow\widehat{\text{A}}+60^0=180^0\\ \Rightarrow\widehat{\text{A}}=120^0\)

Vì \(\widehat{\text{A}}=\widehat{\text{B}}\left(\text{ABCD là hình thang cân}\right)\)

\(\Rightarrow\widehat{\text{A}}=\widehat{\text{B}}=120^0\)

Vậy, số đo các góc trong hình thang cân ABCD là: \(\widehat{\text{A}}=\widehat{\text{B}}=120^0;\widehat{\text{C}}=\widehat{\text{D}}=60^0.\)

\(\text{#3107}\)

1.

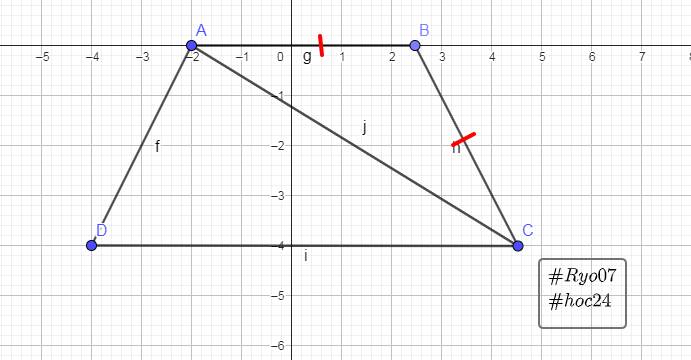
Ta có: \(\text{AB // CD}\)

\(\Rightarrow\widehat{\text{BAC}}=\widehat{\text{ACD}}\left(\text{2 góc sole trong}\right)\) `(1)`

Xét `\Delta ABC:`

\(\text{AB = BC (gt)}\)

\(\Rightarrow\) `\Delta ABC` cân tại B

\(\Rightarrow\widehat{\text{BAC}}=\widehat{\text{BCA}}\) `(2)`

Từ `(1)` và `(2)`

\(\Rightarrow\widehat{\text{ACB}}=\widehat{\text{ACD}}\)

Mà \(\widehat{\text{ACB}}+\widehat{\text{ACD}}=\widehat{\text{BCD}}\)

\(\Rightarrow\) CA là phân giác của \(\widehat{\text{BCD}}.\)

 ai giải hộ vs

giúp với