
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


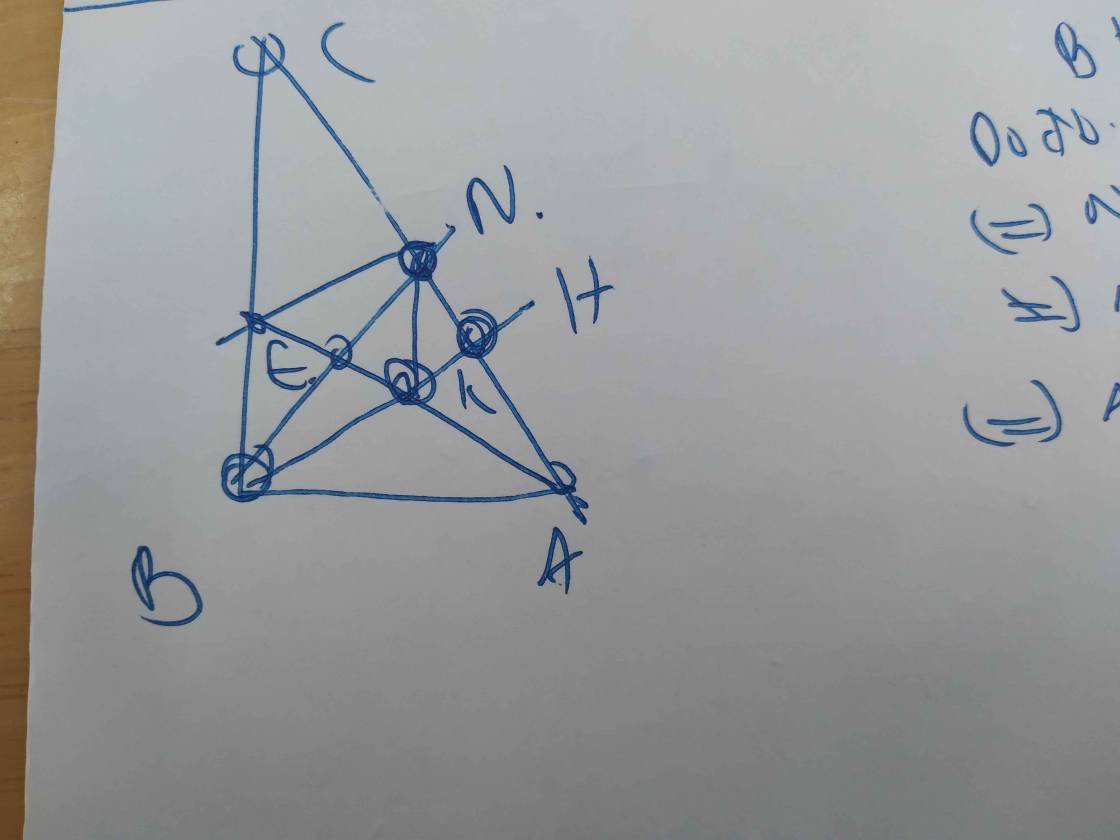
a: Xét ΔKNP vuông tại K và ΔHPN vuông tại H có
PN chung
\(\widehat{KNP}=\widehat{HPN}\)
Do đó: ΔKNP=ΔHPN
b: Ta có: ΔKNP=ΔHPN
=>\(\widehat{KPN}=\widehat{HNP}\)
=>\(\widehat{ENP}=\widehat{EPN}\)
=>ΔENP cân tại E
c: Xét ΔMEN và ΔMEP có
ME chung
EN=EP(ΔENP cân tại E)
MN=MP
Do đó: ΔMEN=ΔMEP
=>\(\widehat{NME}=\widehat{PME}\)
=>ME là phân giác của góc NMP

\(x\cdot\left(x^2-3\right)-x^3+7=0\\ x^3-3x-x^3+7=0\\ -3x+7=0\\ -3x=-7\\ x=\dfrac{7}{3}\)

(2x⁴ - x³ + 3x²) : (-1/3 x²)
= 2x⁴ : (-1/3 x²) - x³ : (-1/3 x²) + 3x² : (-1/3 x²)
= -6x² + 3x - 9
(2\(x^4\) - \(x^3\) + 3\(x^2\)) : (- \(\dfrac{1}{3}\)\(x^2\))
= \(x^2\).(2\(x^2\) - \(x\) + 3) : (\(x^2\)): (\(\dfrac{-1}{3}\))
= (2\(x^2\) - \(x\) + 3) x \(\dfrac{3}{-1}\)
= - 6\(x^2\) +3\(x\) - 9

Tam giác ABC vuông tại B, với BA < BC.
Điểm N trên cạnh AC sao cho AN = AB.
AE là đường vuông góc với BC tại A.
BH là đường cao của tam giác ABC.
Điểm K là giao điểm của BH và AE.
Do tam giác ABC vuông tại B và AN = AB nên tam giác ANB cũng vuông tại N.
Do đó, góc ANB = góc ABC (cùng bằng 90 độ).
Lại có góc ANK = góc ANB (do K nằm trên đường thẳng NB).
Vậy suy ra góc ANK = góc ACB.








\(f\left(5\right)-f\left(4\right)=2022\)
=>\(125a+25b+5c+2021-64a-16b-4c-2021=2022\)
=>61a+9b+c=2022
\(f\left(7\right)-f\left(2\right)\)
\(=343a+49b+7c+2021-8a-4b-2c-2021\)
\(=335a+45b+5c=5\left(61a+9b+c\right)=5\cdot2022\) là hợp số