9 mũ 9 mũ 9

\(9^{9^9}=9^{9.9}=9^{81}\)

a: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có

BD chung

\(\widehat{ABD}=\widehat{MBD}\)

Do đó: ΔBAD=ΔBMD

b: Ta có: ΔBAD=ΔBMD

=>DA=DM

mà DM<DC(ΔDMC vuông tại M)

nên DA<DC

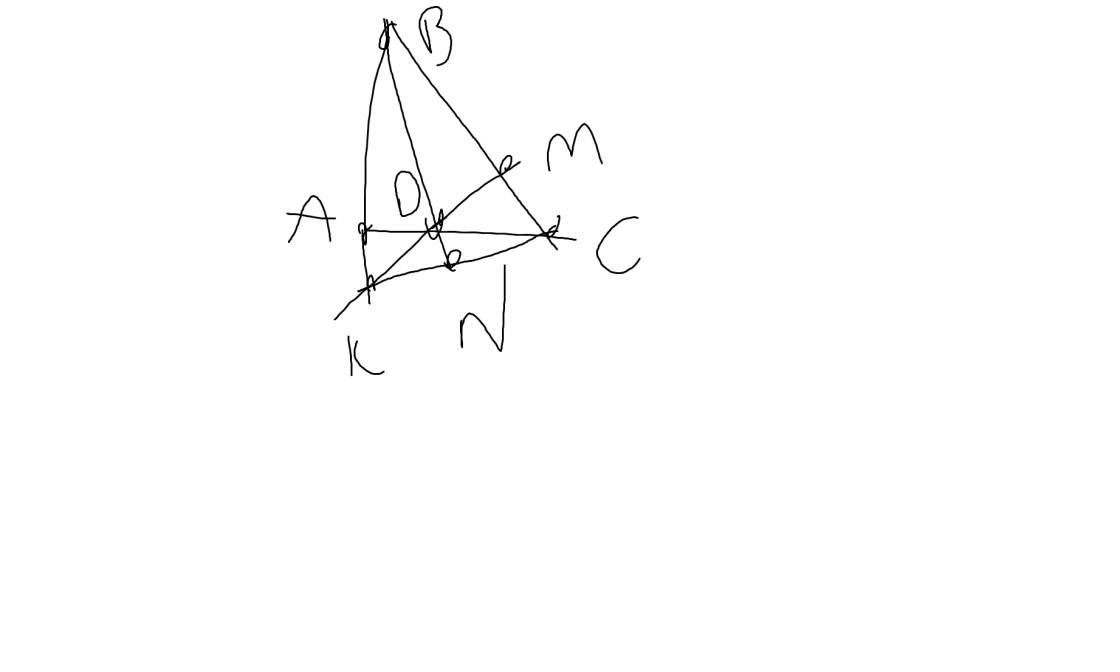
c: Xét ΔBKC có

KM,CA là các đường cao

KM cắt CA tại D

Do đó: D là trực tâm của ΔBKC

=>BD\(\perp\)KC

Xét ΔDAK vuông tại A và ΔDMC vuông tại M có

DA=DM

\(\widehat{ADK}=\widehat{MDC}\)(hai góc đối đỉnh)

Do đó: ΔDAK=ΔDMC

=>DK=DC
=>ΔDKC cân tại D

Gọi số khẩu trang lớp 7A,7B,7C ủng hộ lần lượt là a(cái),b(cái),c(cái)

(Điều kiện: \(a,b,c\in Z^+\))

Số khẩu trang lớp 7A,7B,7C ủng hộ lần lượt tỉ lệ thuận với 3;5;8 nên \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}\)

Tổng số khẩu trang ba lớp ủng hộ được là 256 cái nên a+b+c=256

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}=\dfrac{a+b+c}{3+5+8}=\dfrac{256}{16}=16\)

=>\(a=16\cdot3=48;b=16\cdot5=80;c=16\cdot8=128\)

vậy: số khẩu trang lớp 7A,7B,7C ủng hộ lần lượt là 48 cái; 80 cái ;128 cái

Gọi x, y, z(khẩu trang) lần lượt là số khẩu trang ba lớp 7A, 7B và 7C ủng hộ được
(\(x,y,z\in N\)*)
Do số khẩu trang ủng hộ được của mỗi lớp lần lượt tỉ lệ với các số 3; 5; 8 nên:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{8}\)
Do tổng số khẩu trang ủng hộ được của ba lớp là 256 nên: \(x+y+z=256\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{8}=\dfrac{x+y+z}{3+5+8}=\dfrac{256}{16}=16\)
\(\Rightarrow\left\{{}\begin{matrix}x=16\cdot3=48\\y=16\cdot5=80\\z=16\cdot8=128\end{matrix}\right.\)
Vậy...

Bài 6:

1: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

=>HB=HC

2: Ta có: ΔAHB=ΔAHC

=>\(\widehat{BAH}=\widehat{CAH}\)

Xét ΔAMH vuông tại M và ΔANH vuông tại N có

AH chung

\(\widehat{MAH}=\widehat{NAH}\)

Do đó: ΔAMH=ΔANH

=>MA=AN

=>ΔAMN cân tại A

bài 5:

a: Xét ΔABC có \(\widehat{B}< \widehat{A}< \widehat{C}\)

mà AC,BC,AB lần lượt là cạnh đối diện của các góc ABC,BAC,ACB

nên AC<BC<AB

b: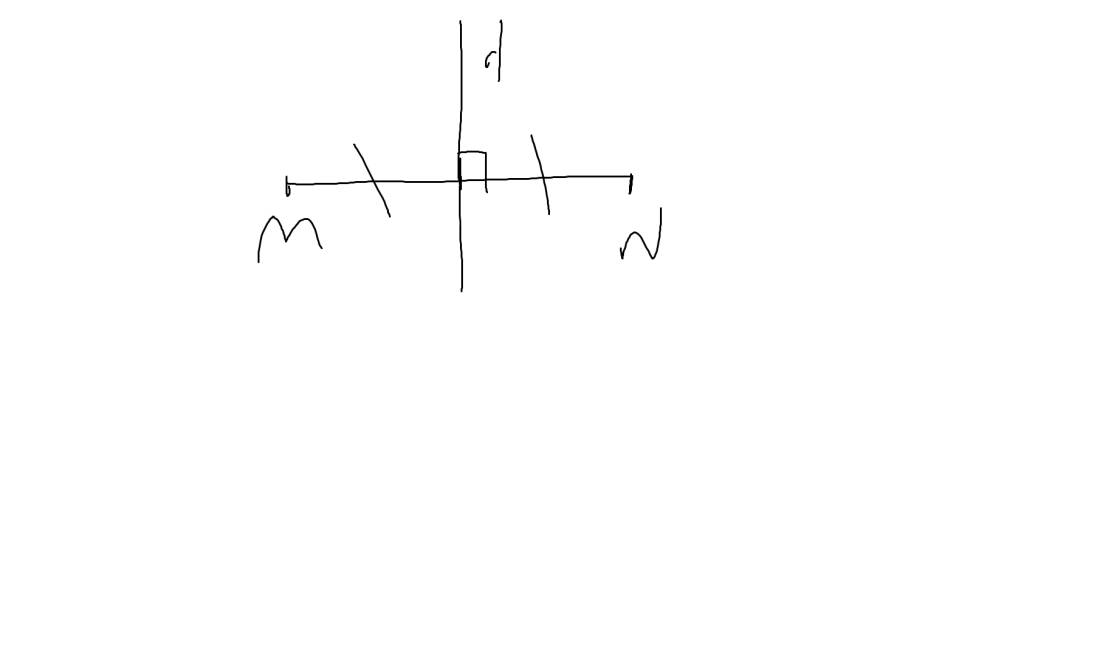 

x=100 nên x+1=101

\(f\left(x\right)=x^8-101x^7+101x^6-...+101x^2-101x\)

\(=x^8-x^7\left(x+1\right)+x^6\left(x+1\right)-...+x^2\left(x+1\right)-x\left(x+1\right)\)

\(=x^8-x^8-x^7+x^7+...+x^3+x^2-x^2-x\)

=-x=-100

Bạn tham khảo nhé:

Bạn xem lại đề bài theo tôi tạm gọi số học sinh khá bằng 5/2 số học sinh giỏi ( không phải 3/2)

Gọi K là số học sinh khá

Gọi G là số học sinh giỏi

Theo đề : 

K =  5/2G

Mà (K - 6) = 2(G+10)

Nên (5/2G – 6) = 2G + 20

 5/2G -6 = 2G + 20

 5/2G – 2G = 26

1/2G = 26

G = 52

Vậy số học sinh giỏi là 52

Gọi số học sinh giỏi khối 7 là x(bạn)

(ĐK: \(x\in Z^+\))

Số học sinh khá khối 7 là \(\dfrac{3}{2}x=1,5x\left(bạn\right)\)

Số học sinh giỏi sau khi thêm 10 bạn là x+10(bạn)

Số học sinh khá sau khi giảm đi 6 bạn là 1,5x-6(bạn)

Theo đề, ta có phương trình:

\(1,5x-6=2\left(x+10\right)\)

=>1,5x-6=2x+20

=>-0,5x=26

=>x=-52

=>Đề sai rồi bạn

A(x) = 2x² - 3x³ + x⁴ - 4x + 1

= x⁴ - 3x³ + 2x² - 4x + 1

B(x) = -3x³ + x⁴ - x² + 2 - 3x + 3x²

= x⁴ - 3x³ + (-x² + 3x²) - 3x + 2

= x⁴ - 3x³ + 2x² - 3x + 2

D(x) = A(x) - B(x)

= (x⁴ - 3x³ + 2x² - 4x + 1) - (x⁴ - 3x³ + 2x² - 3x + 2)

= x⁴ - 3x³ + 2x² - 4x + 1 - x⁴ + 3x³ - 2x² + 3x - 2

= (x⁴ - x⁴) + (-3x³ + 3x³) + (2x² - 2x²) + (-4x + 3x) + (1 - 2)

= -x - 1

c) Cho D(x) = 0

-x - 1 = 0

x = -1

Vậy nghiệm của đa thức D(x) là x = -1

Toán 

a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)

mà AB=AC

nên AM=MB=AN=NC

BE=BD+DE

CD=CE+ED

mà BD=CE

nên BE=CD

Xét ΔMBE và ΔNCD có

MB=NC

\(\widehat{MBE}=\widehat{NCD}\)

BE=CD

Do đó: ΔMBE=ΔNCD

=>ME=ND

b: Ta có: ΔMBE=ΔNCD

=>\(\widehat{MEB}=\widehat{NDC}\)

=>\(\widehat{IDE}=\widehat{IED}\)

=>ID=IE

c: Ta có: \(\widehat{IDE}+\widehat{IDB}=180^0\)

\(\widehat{IED}+\widehat{IEC}=180^0\)

mà \(\widehat{IED}=\widehat{IDE}\)

nên \(\widehat{IDB}=\widehat{IEC}\)

Xét ΔIDB và ΔIEC có

ID=IE

\(\widehat{IDB}=\widehat{IEC}\)

DB=CE

Do đó: ΔIDB=ΔIEC
=>IB=IC

=>I nằm trên đường trung trực của BC(1)

ta có: AB=AC

=>A nằm trên đường trung trực của BC(2)

Từ (1),(2) suy ra AI là đường trung trực của BC

=>AI\(\perp\)BC

còn d thì sAo