Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{-2x^2-2x}{1-x^2}=\dfrac{-2x\left(x+1\right)}{\left(1-x\right)\left(1+x\right)}\)
\(=\dfrac{-2x}{1-x}\)
\(=\dfrac{2x}{x-1}\)
Chọn B và C

ĐKXĐ:
\(2x-6\ne0\)
\(\Leftrightarrow2x\ne6\)
\(\Leftrightarrow x\ne\dfrac{6}{2}\)
\(\Leftrightarrow x\ne3\)
Chọn A


Lời giải:
$A=2x^2+y^2+2xy+2x-2y+2023$
$=(x^2+2xy+y^2)+x^2+2x-2y+2023$
$=(x+y)^2-2(x+y)+x^2+4x+2023$
$=(x+y)^2-2(x+y)+1+(x^2+4x+4)+2018$
$=(x+y-1)^2+(x+2)^2+2018\geq 0+0+2018=2018$
Vậy GTNN của $A$ là $2018$. Giá trị này đạt tại $x+y-1=x+2=0$
$\Leftrightarrow x=-2; y=3$

\(x\).(\(x\) + 2) + (\(x\) + 2)
= \(x\).(\(x\) + 2) + (\(x\) + 2).1
= (\(x\) + 2).(\(x\) + 1)
= (\(x\) + 1).(\(x\) + 2)

Lời giải:
$55^{n+1}-55^2=55^2[55^{n-1}-1]=55^2(55-1)(55^{n-2}+55^{n-3}+...+55+1)$
$=54.55^2(55^{n-2}+55^{n-3}+...+55+1)\vdots 54$
Ta có đpcm.

a)ta có:
AB=DC mà AE=1/2 AB, KC= 1/2 DC
=>AE=KC
Xét tứ giác AECK, ta có:
AE//KC(AB//KC và AE thuộc AB và KC thuộc DC)
=>tứ giác AECK là hình bình hành.
b) chỗ DE vuông góc CE có đúng không vậy để mai mình làm tiếp

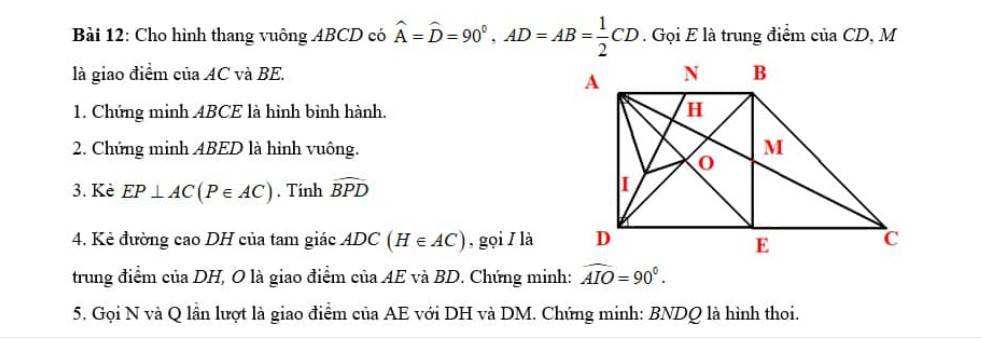
1/
Ta có
\(ÁH\perp BD\left(gt\right);CK\perp BD\left(gt\right)\) => AH//CK (1)
Xét tg vuông ADH và tg vuông BCK có
AD//BC (cạnh đối hbh) \(\Rightarrow\widehat{ADH}=\widehat{CBK}\) (góc so le trong)
AD=BC (cạnh đối hbh)
=> tg ADH = tg BCK (Hai tg cuông có cạnh huyền và góc nhọn tương ứng bằng nhau) => AH=CK (2)
Từ (1) và (2) => AHCK là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
2/
Ta có
AH//CK (cmt) => AI//CF
AB//CD (cạnh đối hbh) => AF//CI
=> AICF là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => AI = CF (cạnh đối hbh)
4/ Xét hbh AHCK có
AC cắt HK tại O' => O'H=O'K (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường) => O' là trung điểm HK
Mà O cũng là trung điểm HK
=> \(O\equiv O'\) => A; O; C thẳng hàng
5/
Xét hbh AHCK có
AC cắt HK tại O (cmt) => OA=OC
Xét hbh ABCD có
OA=OC (cmt) => OB=OD (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Ta có
AICF là hbh (cmt) => FI cắt AC tại trung điểm O của AC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> AC; BD; IF đồng quy
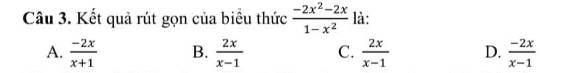
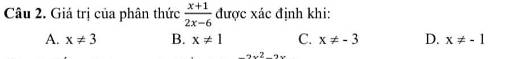
 Chứng minh 55^(n + 1) - 55^2 chia hết cho 54 (với n là số tự nhiên)
Chứng minh 55^(n + 1) - 55^2 chia hết cho 54 (với n là số tự nhiên)
\(\Delta ABC\) vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2\left(Pytago\right)\)
\(=3^2+4^2\)
\(=25\)
\(\Rightarrow BC=5\left(cm\right)\)
Đường trung tuyến AM là đường trung tuyến ứng với cạnh huyền BC
\(\Rightarrow AM=\dfrac{BC}{2}=\dfrac{5}{2}=2,5\left(cm\right)\)
Chọn C