Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d: \(\left|-5-\sqrt{2}\right|=5+\sqrt{2}\)
c: \(\left|4+\sqrt{3}\right|=4+\sqrt{3}\)
d: \(\left|-\dfrac{4}{15}\right|=\dfrac{4}{15}\)
a: \(\left|3,02\right|=3,02\)

a: \(\sqrt{50}>\sqrt{49}\)
mà \(\sqrt{49}=7\)
nên \(\sqrt{50}>7\)
b: \(\sqrt{27}>\sqrt{25}=5\)
=>\(\dfrac{4}{\sqrt{27}}< \dfrac{4}{5}\)
c: \(\dfrac{3}{\sqrt{7}}>1;\dfrac{\sqrt{7}}{3}< 1\)
Do đó: \(\dfrac{3}{\sqrt{7}}>\dfrac{\sqrt{7}}{3}\)

Bài 2:
a:
\(-4,4\left(9\right)-5,8\left(1\right)\simeq-4,5-5,8=-10,3\)
\(-4,4\left(9\right)-5,8\left(1\right)\)
\(=-\dfrac{9}{2}-\dfrac{-523}{90}=-\dfrac{9}{2}+\dfrac{523}{90}=\dfrac{118}{90}=\dfrac{59}{45}\)
b:
\(-12,\left(7\right)\cdot3,\left(12\right)\simeq-12,8\cdot3,1\simeq-40\)
\(-12,\left(7\right)\cdot3,\left(12\right)\)
\(=-\dfrac{115}{9}\cdot\dfrac{103}{33}=\dfrac{11845}{297}\)
c: \(9,\left(49\right):\left[-5,\left(09\right)\right]\simeq9,5:\left(-5,1\right)\simeq-1,9\)
\(9,\left(49\right):\left[-5,\left(09\right)\right]\)
\(=\dfrac{940}{99}:\dfrac{-56}{11}=\dfrac{940}{99}\cdot\dfrac{11}{-56}\)
\(=\dfrac{940}{-56}\cdot\dfrac{1}{9}=-\dfrac{235}{14\cdot9}=-\dfrac{235}{126}\)
Bài 1:
a: \(9,4\simeq9\)
b: \(3,51\simeq4\)
c: \(-7,505\simeq-8\)
d: \(-1.199\simeq-1\)

\(\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\)
=>(a+b)(c-a)=(a-b)(c+a)
=>\(ac-a^2+bc-ba=ac+a^2-bc-ab\)
=>\(-a^2+bc=a^2-bc\)
=>\(-2a^2=-2bc\)
=>\(a^2=bc\)
\[
\frac{a+b}{a-b} = \frac{c+a}{c-a}
\]
Ta sẽ thực hiện phép nhân chéo:
\[
(a+b)(c-a) = (a-b)(c+a)
\]
Khai triển hai vế của phương trình:
- Vế trái:
\[
(a+b)(c-a) = ac - a^2 + bc - ab
\]
- Vế phải:
\[
(a-b)(c+a) = ac + a^2 - bc - ab
\]
Từ đó ta có:
\[
ac - a^2 + bc - ab = ac + a^2 - bc - ab
\]
Giản lược hai vế:
\[
-a^2 + bc = a^2 - bc
\]
Chuyển các hạng tử về cùng một vế:
\[
-a^2 + bc - a^2 + bc = 0
\]
\[
-2a^2 + 2bc = 0
\]
Chia cả hai vế cho 2:
\[
-a^2 + bc = 0
\]
Chuyển \(-a^2\) qua vế phải:
\[
bc = a^2
\]

Xét ΔEDI có \(\widehat{EIF}\) là góc ngoài
nên \(\widehat{EIF}=\widehat{IED}+\widehat{IDE}\)
=>\(\widehat{IED}=110^0-90^0=20^0\)
EI là phân giác của góc DEF
=>\(\widehat{DEF}=2\cdot\widehat{DEI}=40^0\)
ΔDEF vuông tại D
=>\(\widehat{DEF}+\widehat{DFE}=90^0\)
=>\(\widehat{DFE}=90^0-40^0=50^0\)

Sửa đề: \(\dfrac{2^{12}\cdot3^5-4^6\cdot9^2}{2^{12}\cdot9^6+8\cdot9^5}\)
\(=\dfrac{2^{12}\cdot3^5-2^{12}\cdot3^4}{2^{12}\cdot3^{12}+2^3\cdot3^{10}}\)
\(=\dfrac{2^{12}\cdot3^4\left(3-1\right)}{2^3\cdot3^{10}\left(2^9\cdot3^2+1\right)}\)
\(=\dfrac{2^9}{3^6}\cdot\dfrac{2}{1028\cdot9+1}=\dfrac{2^{10}}{729\left(1028\cdot9+1\right)}\)

Bài 2:
a: \(\left|x+\dfrac{1}{5}\right|-\dfrac{1}{2}=\dfrac{9}{10}\)
=>\(\left|x+\dfrac{1}{5}\right|=\dfrac{1}{2}+\dfrac{9}{10}=\dfrac{14}{10}=\dfrac{7}{5}\)
=>\(\left[{}\begin{matrix}x+\dfrac{1}{5}=\dfrac{7}{5}\\x+\dfrac{1}{5}=-\dfrac{7}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\\x=-\dfrac{8}{5}\end{matrix}\right.\)
b: \(\dfrac{5}{4}-3\left|2x+5\right|=\dfrac{3}{4}\)
=>\(3\left|2x+5\right|=\dfrac{5}{4}-\dfrac{3}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)
=>\(\left|2x+5\right|=\dfrac{1}{6}\)
=>\(\left[{}\begin{matrix}2x+5=\dfrac{1}{6}\\2x+5=-\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{1}{6}-5=-\dfrac{29}{6}\\2x=-\dfrac{1}{6}-5=-\dfrac{31}{6}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{29}{12}\\x=-\dfrac{31}{12}\end{matrix}\right.\)
c: \(\left(\dfrac{3}{5}x+\dfrac{1}{2}\right)^2=\dfrac{25}{16}\)
=>\(\left[{}\begin{matrix}\dfrac{3}{5}x+\dfrac{1}{2}=\dfrac{5}{4}\\\dfrac{3}{5}x+\dfrac{1}{2}=-\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\dfrac{3}{5}x=\dfrac{5}{4}-\dfrac{1}{2}=\dfrac{3}{4}\\\dfrac{3}{5}x=-\dfrac{5}{4}-\dfrac{1}{2}=-\dfrac{7}{4}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{3}{4}:\dfrac{3}{5}=\dfrac{5}{4}\\x=-\dfrac{7}{4}:\dfrac{3}{5}=-\dfrac{7}{4}\cdot\dfrac{5}{3}=-\dfrac{35}{12}\end{matrix}\right.\)
d: \(3-\left(2x+1\right)^2=2\)
=>\(\left(2x+1\right)^2=3-2=1\)
=>\(\left[{}\begin{matrix}2x+1=1\\2x+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Bài 1:
a: \(\left(-\dfrac{2}{3}\right)^2\cdot\dfrac{9}{16}-\sqrt{\dfrac{4}{81}}:\dfrac{16}{9}+\left|-0,25\right|\)
\(=\dfrac{4}{9}\cdot\dfrac{9}{16}-\dfrac{2}{9}\cdot\dfrac{9}{16}+\dfrac{1}{4}\)
\(=\dfrac{4}{16}-\dfrac{2}{16}+\dfrac{1}{4}=\dfrac{1}{2}-\dfrac{1}{8}=\dfrac{3}{8}\)
b: \(\left(-2\right)^3+\dfrac{1}{2}:\dfrac{1}{8}-\sqrt{25}+\left|-8\right|\)
\(=-8+\dfrac{1}{2}\cdot8-5+8\)
=4-5=-1
c: \(\left(\dfrac{4}{3}-\dfrac{3}{2}\right)^2-2:\left|-\dfrac{1}{9}\right|+\dfrac{-5}{18}\)
\(=\left(\dfrac{8}{6}-\dfrac{9}{6}\right)^2-2:\dfrac{1}{9}-\dfrac{5}{18}\)
\(=\dfrac{1}{36}-18-\dfrac{5}{18}=\dfrac{1}{36}-\dfrac{10}{36}-18=-\dfrac{9}{36}-18\)
\(=-18-\dfrac{1}{4}=-18,25\)
d: \(\left(-\dfrac{3}{4}\right)^2:\left(-\dfrac{1}{4}\right)^2+9\left(\dfrac{1}{3}\right)^2+\left|-\dfrac{3}{2}\right|\)
\(=\left(-\dfrac{3}{4}:\dfrac{-1}{4}\right)^2+9\cdot\dfrac{1}{9}+\dfrac{3}{2}\)
\(=3^2+1+\dfrac{3}{2}=9+1+\dfrac{3}{2}=10+\dfrac{3}{2}=11,5\)

`A= (x+5)/(x+3 )`
Điều kiện: `x ≠ -3`
Do `x ∈ Z => x + 5` và `x + 3∈ Z`
Để `A ∈ Z <=> x + 5 ⋮x + 3`
`<=> x + 3 + 2 ⋮ x + 3`
Do `x + 3 ⋮ x + 3`
Nên `2 ⋮ x + 3`
`=> x + 3 ∈ Ư(2) =` {`-2;-1;1;2`}
`=> x ∈` {`-5;-4;-2;-1`} (Thỏa mãn)
Vậy ...
------------------------------
`B =(x-2)/(x+1)`
Điều kiện: `x ≠ -1`
Do `x ∈ Z => x -2` và `x + 1 ∈ Z`
Để `B ∈ Z <=> x -2 ⋮x + 1`
`<=> x + 1 - 3 ⋮x + 1`
Do `x + 1 ⋮x + 1`
Nên `3⋮x + 1`
`=> x + 1 ∈ Ư(3) =` {`-3;-1;1;3`}
`=> x ∈` {`-4;-2;0;2`} (Thỏa mãn)
Vậy ...
\(A=\dfrac{x+5}{x+3}\in Z\)
\(\Rightarrow\left(x+5\right)⋮\left(x+3\right)\)
Mà \(\left(x+3\right)⋮\left(x+3\right)\)
\(\Rightarrow\left(x+5\right)-\left(x+3\right)⋮\left(x+3\right)\)
\(\Rightarrow2⋮\left(x+3\right)\)
\(\Rightarrow\left(x+3\right)\inƯ\left(2\right)\)
\(\Rightarrow\left(x+3\right)\in\left\{1;-1;-2;2\right\}\)
Ta có bảng giá trị:
| \(x+3\) | 1 | -1 | 2 | -2 |
| \(x\) | -2 | -4 | -1 | -5 |
Vậy \(x\in\left\{-2;-4;-1;-5\right\}\)
Những câu còn lại, cách làm tương tự, nếu như còn thắc mắc thì bạn tag mình nhé.

a: AF//BE
AF\(\perp\)AC
Do đó: BE\(\perp\)AC
b: Vì \(\widehat{F}=\widehat{EDC}\left(=75^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//CD
mà AF\(\perp\)AB
nên CD\(\perp\)AB
=>\(\widehat{C_1}=90^0\)
Ta có: BE//AF
=>\(\widehat{E_2}=\widehat{F}=75^0\)
Ta có: \(\widehat{E_1}+\widehat{E_2}=180^0\)(hai góc kề bù)
=>\(\widehat{E_1}=180^0-75^0=105^0\)
Vì BE\(\perp\)AC
nên \(\widehat{B_1}=90^0\)
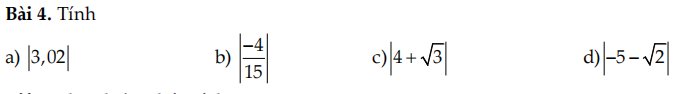
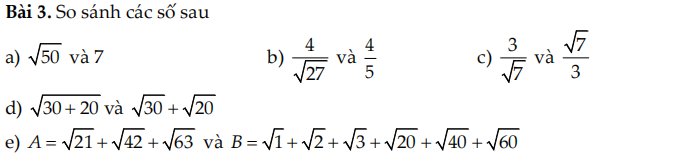


a: \(\left|-\dfrac{1}{3}\right|-\left(-\dfrac{6}{7}\right)^0+\left(\dfrac{1}{2}\right)^2:2\)
\(=\dfrac{1}{3}-1+\dfrac{1}{4}:2=-\dfrac{2}{3}+\dfrac{1}{8}=\dfrac{-16}{24}+\dfrac{3}{24}=-\dfrac{13}{24}\)
b: \(\left(\dfrac{2}{3}\right)^3+\sqrt{\dfrac{49}{81}}-\left|-\dfrac{7}{3}\right|:3\)
\(=\dfrac{8}{27}+\dfrac{7}{9}-\dfrac{7}{3}\cdot\dfrac{1}{3}\)
\(=\dfrac{8}{27}+\dfrac{7}{9}-\dfrac{7}{9}=\dfrac{8}{27}\)
c: \(\sqrt{\dfrac{25}{49}}+\left(5555\right)^0+\left|-\dfrac{2}{7}\right|\)
\(=\dfrac{5}{7}+1+\dfrac{2}{7}\)
=1+1=2