bạn an đọc hết 1 cuốn sách hết 3 ngày,ngày thứ nhất đọc 1/3 số trang,ngày thứ 2 đọc 5/8 số trang còn lại,ngày thứ 3 đọc hết 30 trang. a)hỏi quyển sách có bao nhiêu trang b)tính số trang đọc dược của ngày thứ nhất/ngày thứ 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bước 1: Xét tổng P
Tổng \(P\) có dạng một chuỗi luân phiên (các số hạng dương và âm xen kẽ), có thể được viết lại dưới dạng:
\(P = \left(\right. 1 - \frac{1}{2} \left.\right) + \left(\right. \frac{1}{3} - \frac{1}{4} \left.\right) + \hdots + \left(\right. \frac{1}{2023} - \frac{1}{2024} \left.\right)\)Mỗi cặp số hạng có dạng:
\(\frac{1}{k} - \frac{1}{k + 1} = \frac{k + 1 - k}{k \left(\right. k + 1 \left.\right)} = \frac{1}{k \left(\right. k + 1 \left.\right)}\)Vậy tổng của tất cả các cặp từ 1 đến 2023 là:
\(P = \sum_{k = 1}^{2023} \frac{1}{k} - \sum_{k = 1}^{2023} \frac{1}{k + 1}\)Tổng này gần giống với tổng điều hòa \(H_{n}\) (mà \(H_{n} sim ln n\)), và có thể xấp xỉ:
\(P \approx ln 2024 - ln 2 = ln \frac{2024}{2} = ln 1012\)Bước 2: Xét tổng Q
Tổng \(Q\) là một phần của tổng điều hòa từ 1013 đến 2024:
\(Q = \sum_{k = 1013}^{2024} \frac{1}{k}\)Xấp xỉ tổng điều hòa:
\(Q \approx ln 2024 - ln 1012 = ln \frac{2024}{1012} = ln 2\)Bước 3: So sánh P và Q
Từ các kết quả trên, ta thấy:
\(P \approx ln 1012 , Q \approx ln 2\)Vì \(ln 1012\) lớn hơn \(ln 2\) rất nhiều (\(ln 1012 \approx 7\), trong khi \(ln 2 \approx 0.693\)), ta có:
\(P > Q\)Kết luận:
\(P > Q\) 4o
a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB=OB-OA=10-4=6(cm)
b: C là trung điểm của AB
=>\(CA=CB=\dfrac{AB}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Vì AO và AB là hai tia đối nhau
mà C thuộc tia AB
nên AO và AC là hai tia đối nhau
=>A nằm giữa O và C
=>OC=OA+AC=4+3=7(cm)
Đề bài của bạn không bảo nó là tia gì mình gọi nó là tia Ox cho dễ làm nhé :
a ) Điểm A nằm giữa 2 điểm còn lại vì :
+ ) OA < OB ( 10 cm > 4 cm )
+ ) Cả ba điểm O , A , B cùng nằm trên tia Ox
Vì A nằm giữa 2 điểm O và B nên ta có :
AB = OB - OA
AB = 10 - 4 = 6 (cm)
b )Vì C là trung điểm của AB nên ta có
AC = CB = 1/2 . AB = 1/2 . 6 = 3 ( cm)
Vì A nằm giữa O và C nên ta có :
OC = OA + AC
OC = 4 +3 = 7 ( cm )
Vậy a) điểm A Nằm giữa 2 điểm còn lại và AB dài 6 ( cm )
b ) Độ dài đoạn thẳng OC là 7 cm
Xin lỗi vì mình không vẽ được hình

Diện tích cái sân hình vuông: 27 x 27 = 729 (m2)
Chiều dài thửa ruộng HCN: 729 : 22,5 = 32,4(m)
Chu vi thửa ruộng HCN: (32,4 + 22,5) x 2 = 109,8 (m)
Đáp số: 109,8m

Gọi diện tích cánh đồng là x(ha)
(Điều kiện: x>0)
Sau ngày thứ nhất thì diện tích còn lại của cánh đồng là:
\(x\cdot50\%-3=0,5x-3\left(ha\right)\)
9 ha cuối cùng chiếm:
100%-25%=75%(diện tích phần còn lại)
=>\(0,5x-3=9:75\%=12\)
=>0,5x=15
=>x=30(nhận)
Vậy: Diện tích cánh đồng là 30ha
Giải:
9ha ứng với: 100% - 25% = 75% (phần còn lại của cánh đồng)
Phần còn lại của cánh đồng là: 9 : 75 x 100 = 12(ha)
Nếu ngày thứ nhất chỉ cày 50% cánh đồng thì còn:
12 + 3 = 15(ha)
15ha ứng với: 100% - 50% = 50% (cánh đồng)
Diện tích cánh đồng là: 15 : 50 x 100 = 30(ha)
Kết luận: Diện tích cánh đồng là: 30ha.

gọi x và y (kg) lần lượt là số gạo của thùng thứ nhất và thùng thứ 2 (đk 0 < x; y < 60)
số gạo ban đầu là: x + y = 60 (1)
theo đề nếu lấy 25% số gạo thùng thứ 1 chuyển sang thùng thứ 2 thì số gạo bằng nhau nên:
x - 25%x = y + 25%x hay 0,75x = y + 0,25x
=> y = 0,75x - 0,25x = 0,5x
thay vào (1) ta được: x + 0,5x = 60
1,5x = 60 => x = 60 : 1,5 = 40 (kg)
=> y = 60 - x = 60 - 40 = 20 (kg)
vậy số gạo của thùng thứ nhất và thùng thứ 2 lần lượt là: 40kg và 20kg
Giải:
Gọi số gạo của thùng thứ nhất là \(x\) (kg); \(x>0\)
Sau khi cho số gạo thùng thứ nhất bằng số gạo thùng thứ hai là:
100%\(x-25\%x=75\%x\) (kg)
Số gạo thùng thứ hai lúc đầu là: 75%\(x\) - 25%\(x\) = 50%\(x\)(kg)
Theo bài ra ta có phương trình: 100%\(x\) + 50%\(x\) = 60
150%\(x\) = 60
\(x\) = 60: 150%
\(x\) = 40(kg)
Số gạo thùng thứ hai lúc đầu là: 60 - 40 = 20 (kg)
Kết luận thùng một lúc đầu có 40 kg gạo.
Thùng hai lúc đầu có 20 kg gạo.

Số các số tự nhiên lẻ có 3 chữ số có thể tính như sau:
Chữ số hàng trăm có thể là một trong các số từ 1 đến 9, nên có 9 lựa chọn. Chữ số hàng chục có thể là bất kỳ số nào từ 0 đến 9, do đó có 10 lựa chọn. Chữ số hàng đơn vị phải là một số lẻ, tức là một trong các số 1, 3, 5, 7, 9, nên có 5 lựa chọn.
Vậy tổng số các số tự nhiên lẻ có 3 chữ số là:
\(9 \times 10 \times 5 = 450\)Vậy có 450 số tự nhiên lẻ có 3 chữ số.
like mình nhé

A = \(-\frac{3}{2.5}\) + \(\frac{-3}{5.8}\) + \(-\frac{3}{8.11}\) + ....+ \(-\frac{3}{97.100}\)
A = - (\(\frac{3}{2.5}\) + \(\frac{3}{5.8}\) + \(\frac{3}{8.11}\) + ... + \(\frac{3}{97.100}\))
A = - (\(\frac12-\frac15\) + \(\frac18\) - \(\frac{1}{11}\) + ...+ \(\frac{1}{97}-\frac{1}{100}\))
A = - \(\frac12\) + \(\frac{1}{100}\)
A = \(-\frac{49}{100}\)

\(a.\dfrac{x}{7}=\dfrac{-4}{14}\)
\(x\times14=-4\times7\)
\(x=\dfrac{-4\times7}{14}\)
\(x=-2\)
Vậy \(x=-2\)
\(b,\dfrac{x+3}{2}=\dfrac{-12}{-6}\dfrac{ }{ }\)
\(\dfrac{x+3}{2}=2\)
\(x+3=2\times2\)
\(x+3=4\)
\(x=4-3\)
\(x=1\)
Vậy \(x=1\)
\(c,\dfrac{x}{2}=\dfrac{-2}{-x}\)
\(\dfrac{x}{2}=\dfrac{2}{x}\)
\(x^2-2\times2\)
\(x^2=4\)
\(x^2=2^2\) hoặc \(x^2=\left(-2\right)^2\)
\(x=2\) \(x=-2\)
Vậy \(x\in\left\{2;-2\right\}\)
\(d,\dfrac{x-1}{5}=\dfrac{5}{x-1}\)
\(\left(x-1\right)^2=5\times5\)
\(\left(x-1\right)^2=25\)
\(\left(x-1\right)^2=5^2\) hoặc \(\left(x-1\right)^2=\left(-5\right)^2\)
\(x-1=5\) \(x-1=-5\)
\(x=5+1\) \(x=-5+1\)
\(x=6\) \(x=-4\)
Vậy \(x\in\left\{6;-4\right\}\)
\(a;\dfrac{x}{7}=-\dfrac{4}{14}\\ =>x=\dfrac{\left(-4\right)\cdot7}{14}=-2\\ b;x+\dfrac{3}{2}=\dfrac{-12}{-6}\\ =>x=\dfrac{1}{2}+\dfrac{3}{2}=\dfrac{1}{2}\\ c;\dfrac{x}{2}=\dfrac{-2}{-x}< =>\dfrac{x}{2}=\dfrac{2}{x}\\ =>x^2=4=>x=\pm2\\ d;\dfrac{x-1}{5}=\dfrac{5}{x-1}\\ =>\left(x-1\right)^2=25\\ =>\left[{}\begin{matrix}x-1=5=>x=6\\x-1=-5=>x=-4\end{matrix}\right.\)
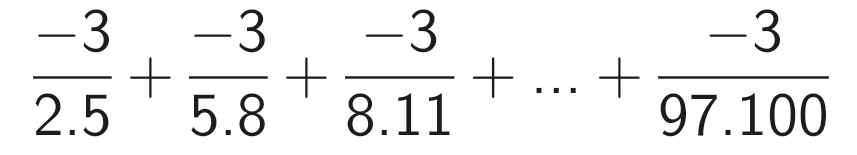
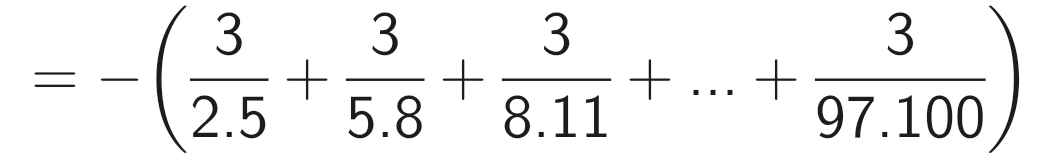
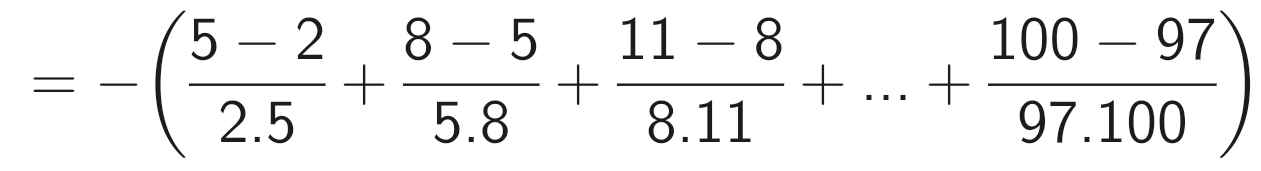
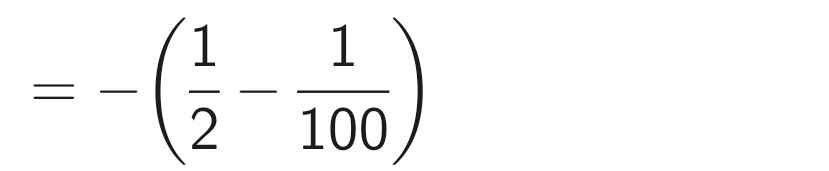
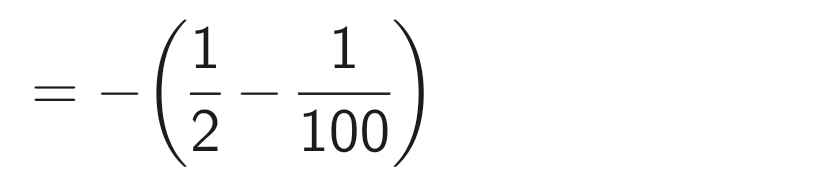

Để giải bài toán này, chúng ta sẽ phân tích từng phần.
a) Hỏi quyển sách có bao nhiêu trang
Kết luận: Quyển sách có 120 trang.
b) Tính số trang đọc được của ngày thứ nhất/ngày thứ hai
Kết quả cuối cùng
a. số phần quyển sách còn lại trong ngày thứ 2 là:
\(\dfrac{5}{8}\cdot\left(1-\dfrac{1}{3}\right)=\dfrac{5}{12}\left(phần\right)\)
số phần trang còn lại trong ngày thứ 3 là:
\(1-\dfrac{1}{3}-\dfrac{5}{12}=\dfrac{1}{4}\left(phần\right)\)
số trang quyển sách có là: \(30:\dfrac{1}{4}=120\left(trang\right)\)
b. số trang đọc được ngày thứ nhất: \(120\cdot\dfrac{1}{3}=40\left(trang\right)\)
số trang đọc được ngày thứ 2: \(120\cdot\dfrac{5}{12}=50\left(trang\right)\)