cứu e với 6h30 hc ròi nuh
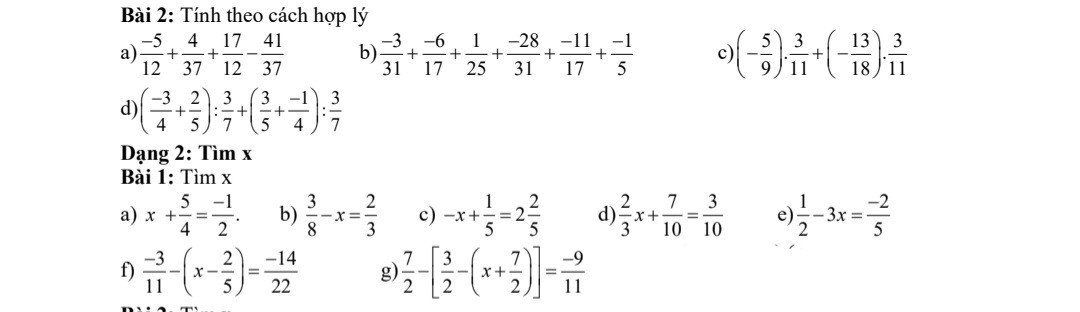
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1; 13 x 58 x 4 + 32 x 26 x 2 + 52 x 10
= (13 x 4) x 58 + 32 x (26 x 2) + 52 x 10
= 52 x 58 + 32 x 52 + 52 x 10
= 52 x (58 + 32 + 10)
= 52 x (90 + 10)
= 52 x 100
= 5200
2; 15 x 37 x 4 + 120 x 21 + 21 x 5 x 12
= (15 x 4) x 37 + 60 x (2 x 21) + (5 x 12) x 21
= 60 x 37 + 60 x 42 + 60 x 21
= 60 x (37 + 42 + 21)
= 60 x (79 + 21)
= 60 x 100
= 6000

a: \(209-18\cdot3+578:17\)
\(=209-54+34\)
=209-20=189
b: \(29-\left[16+3\cdot\left(51-49\right)\right]\)
\(=29-16-3\cdot2\)
=13-6
=7
c: \(80-\left[130-\left(58+2\cdot3\right)\right]\)
\(=80-\left[130-58-6\right]\)
\(=80-130+58+6\)
=64-50=14
d: \(4824-4824:24+12\)
=4836-201
=4635

\(3^{n-2}=27\\ 3^3=27\Rightarrow n-2=3\\ n=3+2\\ n=5\)
Vậy n=5
em đưa về bài toán 2 lũy thừa cùng cơ số (3)
vậy 2 số mũ: n - 2 = 3
n = 5

Gọi số cam ban đầu trong rổ là \(x\) (quả) \(\left(x\inℕ^∗\right)\)
Theo đề bài ta có:
\(x-\left(\dfrac{3}{5}x+5\right)=9\)
\(\Rightarrow x-\dfrac{3}{5}x-5=9\)
\(\Rightarrow x-\dfrac{3}{5}x=9+5\)
\(\Rightarrow\dfrac{2}{5}x=14\)
\(\Rightarrow x=14:\dfrac{2}{5}\)
\(\Rightarrow x=35\) (thỏa mãn điều kiện)
Vậy...
9 quả còn lại cộng 5 quả = 14 quả sẽ bằng \(\dfrac{2}{5}\) số cam
Số cam ban đầu ở rổ: 14: \(\dfrac{2}{5}\) = 35 quả

Tổng số tiền Hà đã dùng là:
`24+36=60` (nghìn đồng)
Số tiền mà mẹ Hà cho Hà là:
`60:1/3=180` (nghìn đồng)
ĐS: ...

\(\left(5^{56}+5^7\right):\left(5^{49}+1\right)\)
\(=5^7\cdot\left(5^{49}+1\right):\left(5^{49}+1\right)\)
\(=5^7\)
\(=78125\)
\(\dfrac{5^{56}+5^7}{5^{49}+1}=\dfrac{5^7\left(1+5^{49}\right)}{1+5^{49}}=5^7\)

Bạn ấn vào biểu tượng Σ bên góc trái màn hình để nhập các công thức toán học bạn nhé!

\(1+2+3+...+x=55\)
=>\(x\cdot\dfrac{\left(x+1\right)}{2}=55\)
=>x(x+1)=110
=>\(x^2+x-110=0\)
=>(x+11)(x-10)=0
=>\(\left[{}\begin{matrix}x+11=0\\x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-11\left(loại\right)\\x=10\left(nhận\right)\end{matrix}\right.\)
Vậy: x=10
\(1+2+3+...+x=55\)
\(\dfrac{x\left(x+1\right)}{2}=55\)
\(x\left(x+1\right)=2\cdot55=110\)
\(x^2+x-110=0\)
\(x^2-10x+11x-110=0\\ x\left(x-10\right)+11\left(x-10\right)=0\\ \left(x-10\right)\left(x+11\right)=0\\ \left[{}\begin{matrix}x=10\\x=-11\end{matrix}\right.\)
Bài 1:
a: \(x+\dfrac{5}{4}=\dfrac{-1}{2}\)
=>\(x=-\dfrac{1}{2}-\dfrac{5}{4}=-\dfrac{2}{4}-\dfrac{5}{4}=-\dfrac{7}{4}\)
b: \(\dfrac{3}{8}-x=\dfrac{2}{3}\)
=>\(x=\dfrac{3}{8}-\dfrac{2}{3}=\dfrac{9}{24}-\dfrac{16}{24}=-\dfrac{7}{24}\)
c: \(-x+\dfrac{1}{5}=2\dfrac{2}{5}\)
=>\(\dfrac{1}{5}-x=\dfrac{12}{5}\)
=>\(x=\dfrac{1}{5}-\dfrac{12}{5}=-\dfrac{11}{5}\)
d: \(\dfrac{2}{3}x+\dfrac{7}{10}=\dfrac{3}{10}\)
=>\(x\cdot\dfrac{2}{3}=\dfrac{3}{10}-\dfrac{7}{10}=-\dfrac{4}{10}=-\dfrac{2}{5}\)
=>\(x=-\dfrac{2}{5}:\dfrac{2}{3}=-\dfrac{2}{5}\cdot\dfrac{3}{2}=-\dfrac{3}{5}\)
e: \(\dfrac{1}{2}-3x=-\dfrac{2}{5}\)
=>\(3x=\dfrac{1}{2}+\dfrac{2}{5}=\dfrac{5}{10}+\dfrac{4}{10}=\dfrac{9}{10}\)
=>\(x=\dfrac{9}{10}:3=\dfrac{3}{10}\)
f: \(\dfrac{-3}{11}-\left(x-\dfrac{2}{5}\right)=-\dfrac{14}{22}\)
=>\(\dfrac{-3}{11}-\left(x-\dfrac{2}{5}\right)=-\dfrac{7}{11}\)
=>\(x-\dfrac{2}{5}=-\dfrac{3}{11}+\dfrac{7}{11}=\dfrac{4}{11}\)
=>\(x=\dfrac{4}{11}+\dfrac{2}{5}=\dfrac{20}{55}+\dfrac{22}{55}=\dfrac{42}{55}\)
g: \(\dfrac{7}{2}-\left[\dfrac{3}{2}-\left(x+\dfrac{7}{2}\right)\right]=-\dfrac{9}{11}\)
=>\(\dfrac{7}{2}-\dfrac{3}{2}+x+\dfrac{7}{2}=-\dfrac{9}{11}\)
=>\(x+\dfrac{11}{2}=-\dfrac{9}{11}\)
=>\(x=-\dfrac{9}{11}-\dfrac{11}{2}=\dfrac{-18}{22}-\dfrac{121}{22}=\dfrac{-139}{22}\)