Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


y³ - 8 - 6y(y - 2)
= (y³ - 8) - 6y(y - 2)
= (y - 2)(y² + 2y + 4) - 6y(y - 2)
= (y - 2)(y² + 2y + 4 - 6y)
= (y - 2)(y² - 4y + 4)
= (y - 2)(y - 2)²
= (y - 2)³
y³ - 8 - 6y(y - 2)
= (y³ - 8) - 6y(y - 2)
= (y - 2)(y² + 2y + 4) - 6y(y - 2)
= (y - 2)(y² + 2y + 4 - 6y)
= (y - 2)(y² - 4y + 4)
= (y - 2)(y - 2)²

P = \(\dfrac{2x+3}{x+3}\) (đk \(x\ne\) - 3; \(x\in\) Z-
P \(\in\) Z ⇔ 2\(x\) + 3 ⋮ \(x\) + 3
2\(x\) + 6 -3 ⋮ \(x\) + 3
2.(\(x\) + 3) - 3 ⋮ \(x\) + 3
3 \(⋮\) \(x\) + 3
\(x\) + 3 \(\in\) Ư(3) = {-3; -1; 1; 3}
Lập bảng ta có:
| \(x\) + 3 | - 3 | -1 | 1 | 3 |
| \(x\) | -6 | -4 | -2 | 0 |
Vì \(x\) \(\in\) Z- nên theo bảng trên ta có:
\(x\) \(\in\) {- 6; - 4; -2}


Lời giải:
b. Ta thấy: $5^2+12^2=13^2$ hay $AB^2+AC^2=BC^2$ nên tam giác $ABC$ vuông tại $A$.
Tứ giác $ACEB$ có 2 đường chéo $BC,AE$ cắt nhau tại trung điểm $D$ của mỗi đường nên là hình bình hành.
Mà $\widehat{A}=90^0$ nên $ACEB$ là hình chữ nhật.
a.
$ACEB$ là hcn nên $AE=BC=13$ (cm)
$\Rightarrow AD=AE:2=13:2=6,5$ (cm)
c.
Để $ABEC$ là hình vuông thì $AB=AC$. Khi đó $ABC$ phải là tam giác vuông cân tại A chứ không liên quan gì đến điểm D hết bạn nhé.

Bài 4:
Quãng đường bạn An đi: $BD$
Quãng đường bạn Hải đi: $CD$
Do $AB\parallel NC$ nên áp dụng định lý Talet, tỉ số quãng đường bạn An đi so với bạn Hải đi là:
$\frac{BD}{CD}=\frac{AB}{NC}=\frac{AB}{AM}=\frac{1}{2}$
Vậy bạn An đi quãng đường bằng 1/2 quãng đường Hải đi
Mà vận tốc 2 bạn như nhau nên thời gian An đi bằng 1/2 thời gian Hải đi
Bạn An đến D lúc 8h, xuất phát từ 7h30 nên thời gian An đi là: 8h-7h30'=30'=0,5h
Thời gian Hải đi để đến gặp An lúc 8h là: $0,5.2=1$ (h)
Vậy Hải phải xuất phát lúc: $8h-1h=7h$
Bài 3:
a. Xét tam giác $ADC$ có $MP\parallel DC$ nên áp dụng định lý Talet:
$\frac{AM}{MD}=\frac{AP}{PC}(1)$
Xét tam giác $ACB$ có $PN\parallel AB$ nên áp dụng định lý Talet:
$\frac{AP}{PC}=\frac{BN}{NC}(2)$
Từ $(1); (2)\Rightarrow \frac{AM}{MD}=\frac{BN}{NC}$
b.
Áp dụng định lý Talet với tam giác $ADC$, $MP\parallel DC$:
$\frac{MP}{DC}=\frac{AM}{AD}=\frac{AM}{AM+MD}=\frac{AM}{AM+2AM}=\frac{1}{3}$
$\Rightarrow MP=DC:3=6:3=2$ (cm)
Theo kết quả phần a:
$\frac{BN}{NC}=\frac{AM}{MD}=\frac{AM}{2AM}=\frac{1}{2}$
$\Rightarrow NC=2BN$
Áp dụng định lý Talet cho tam giác $ACB$, có $PN\parallel AB$:
$\frac{PN}{AB}=\frac{CN}{CB}=\frac{CN}{CN+BN}=\frac{2BN}{2BN+BN}=\frac{2}{3}$
$\Rightarrow PN=\frac{2}{3}AB=\frac{2}{3}.4=\frac{8}{3}$ (cm)
$MN=MP+PN=2+\frac{8}{3}=\frac{14}{3}$ (cm)

Ta có
\(\dfrac{BM}{AM}=\dfrac{BC}{AC}=\dfrac{a}{b}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
\(\dfrac{CN}{AN}=\dfrac{BC}{AB}=\dfrac{a}{b}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
\(\Rightarrow\dfrac{BM}{AM}=\dfrac{CN}{AN}\Rightarrow\dfrac{BM}{CN}=\dfrac{AM}{AN}\) => MN//BC (Talet)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MN}{BC}\Rightarrow\dfrac{AM}{b}=\dfrac{MN}{a}\) (1)
Ta có
\(\dfrac{AM}{BM}=\dfrac{AC}{BC}=\dfrac{b}{a}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
\(\Rightarrow\dfrac{AM}{b}=\dfrac{BM}{a}=\dfrac{AM+BM}{a+b}=\dfrac{AB}{a+b}=\dfrac{b}{a+b}\)
\(\Rightarrow AM=\dfrac{b^2}{a+b}\) Thay vào (1)
\(\Rightarrow\dfrac{\dfrac{b^2}{a+b}}{b}=\dfrac{MN}{a}\Rightarrow\dfrac{b}{a+b}=\dfrac{MN}{a}\Rightarrow MN=\dfrac{ab}{a+b}\)
Ta có
(Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
(Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
=> MN//BC (Talet)
(1)
Ta có
(Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
Thay vào (1)

3x² + 2x - 1
= 3x² + 3x - x - 1
= (3x² + 3x) - (x + 1)
= 3x(x + 1) - (x + 1)
= (x + 1)(3x - 1)

\(\left(-\dfrac{3x}{5y^2}\right).\left(-\dfrac{5y^2}{6x^3}\right)\)
\(=\dfrac{-3x.\left(-5y^2\right)}{5y^2.6x^3}\)
\(=\dfrac{1}{2x^2}\)

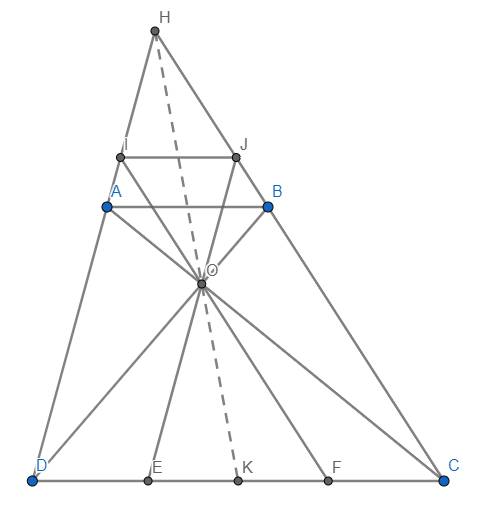
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)
Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)
c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)
Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\)
Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB
d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)

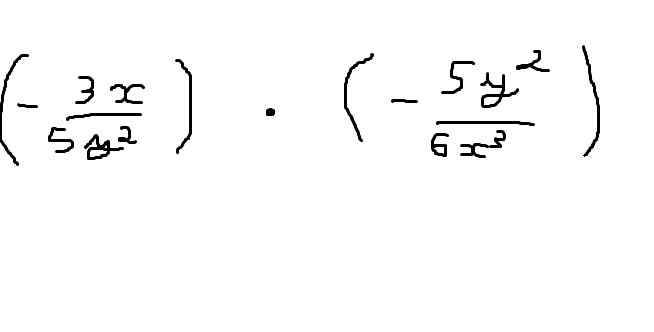
Tọa độ điểm M bị lỗi rồi. Bạn xem lại.