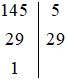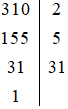Trong tháng 9 nhà bạn Mai dùng hết 205 số điện. Hỏi nhà bạn Mai phải trả bao nhiêu tiền điện, biết đơn giá điện như sau:
Giá tiền cho 50 số đầu tiên là 1678 đồng/số.
Giá tièn cho 50 số tiếp theo (từ số 51 đến số 100) là 1731 đồng/số.
Giá tiền cho 100 số tiếp theo (từ số 101 đến 200) là 2014 đồng/số.
Giá tiền cho 100 số tiếp theo (từ số 201 đến 300) là 2536 đồng/số.