tìm số có ba chữ số , biết rằng khi viết thêm chữ số 3 vào bên phải số đó thì được số mới có bốn chữ số hơn số phải tìm là 4053.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Nửa chu vi của hình chữ nhật là: 74 : 2 = 37 (m)
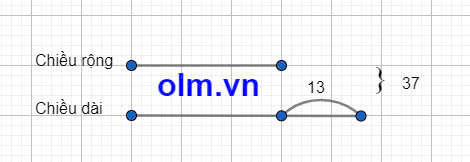
Ta có sơ đồ
Theo sơ đồ ta có:
Chiều rộng là: (37 - 13) : 2 = 12 (m)
Chiều dài là: 12 + 13 = 25 (m)
Diện tích hình chữ nhật là: 25 x 12 = 300 (m\(^2\) )
Diện tích trồng cây cảnh là: 300 x 15% = 45 (m\(^2\) )
Diện tích đất làm nhà là: 300 - 45 = 255 (m\(^2\))
Đáp số: 255m\(^2\)

45,5 x 3 + 45,5 : 0,2 - 45,5 x 2 + 45,5 : \(\frac14\)
= 45,5 x 3 + 45,5 x 5 - 45,5 x 2 + 45,5 x 4
= 45,5 x (3+ 5 - 2 + 4)
= 45,5 x (8 - 2 + 4)
= 45,5 x (6 + 4)
= 45,5 x 10
= 455

Giải:
Tổng số thóc hai kho là: 225 x 2 = 450 (tấn)
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số thóc kho B là: (450 + 300) : 2 = 375 (tấn)
Số thóc kho A là: 450 - 375 = 75 (tấn)
Tỉ phần trăm số thóc kho A và số thóc kho B là:
75 : 375 = 0,2
0,2 = 20%
Đáp số: 20%

Đây là toán nâng cao chuyên đề tổng hiệu ẩn hiệu, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Vì chỉ chuyển từ thùng thứ nhất sang thùng thứ hai 100l nên tổng số dầu hai thùng lúc sau không đổi và bằng lúc đầu là: 2700 l
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Thùng dầu thứ hai lúc sau là: (2700 + 500) : 2 = 1600 (l)
Thùng dầu thứ hai lúc đầu là: 1600 - 100 = 1500 (l)
Thùng dầu thứ nhất lúc đầu có số dầu là: 2700 - 1500 = 1200 (l)
Tỉ số phần trăm số dầu thùng thứ nhất lúc đầu và số dầu thùng thứ hai lúc đầu là:
1200 : 1500 = 0,8
0,8 = 80%
Đáp số 80%

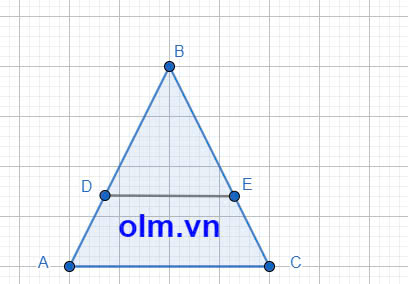
Các tỉ số theo định lí Thales là:
1; \(\frac{BD}{BA}\) = \(\frac{BE}{AC}\)
2; \(\frac{BD}{DA}\) = \(\frac{BE}{EC}\)
3; \(\frac{DA}{BA}\) = \(\frac{EC}{BC}\)

Olm chào em, đây là toán nâng cao chuyên đề bài toán bậc thang, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Từ tầng một lên tầng bốn có số khoảng là:
4 - 1 = 3 (khoảng)
Mỗi khoảng có số bậc là: 81 : 3 = 27 (bậc)
Từ tầng một lên tầng chín có số khoảng là:
9 - 1 = 8 (khoảng)
Từ tầng một để lên đến tầng chín cần phải đi số bậc là:
27 x 8 = 216 (bậc)
Đáp số : 216 bậc
cần số bậc thang để lên mỗi tầng là:
81 : 3 = 27 (bậc)
Cần số bậc thang để lên tầng 9 là:
27 x 9 = 243 (bậc)
đáp số: 243 bậc thang




Đây là dạng toán nâng cao chuyên đề lập số theo điều kiện cho trước. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng sơ đồ đoạn thẳng như sau:
Giải:
Vì viết thêm chữ số 3 vào bên phải số đó thì được số mới nên số mới gấp 10 lần số cũ và 3 đơn vị
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số cũ có ba chữ số cần tìm là: (4053 - 3) : (10 - 1) =450
Đáp số: 450.
pls giúp mình với