Cx k khó lắm vẽ hình chứ bn tự làm đc nhỉ:)) mình làm câu a vs B th nha mấy câu kia vẽ rắc rối lắm lười vẽ=))
                                                Bài Làm
a) Áp dụng quan hệ giữa cạnh và đường cao trong tam giác vuông vào tam giác AHC vuông tại H ( H vuông góc BC ) :
                    \(\Rightarrow\) AH²= AE.AC ( đpcm ) (1)
Áp dụng quan hệ giữa cạnh và đường cao trong tam giác vuông vào tam giác AHB vuông tại H ( H vuông góc BC ) :
                   \(\Rightarrow\)AH²=AD.AB ( đpcm ) ( 2 )
b) Từ (1) và (2) ta có : AE.AC = AD.AB
                               \(\Rightarrow\)\(\dfrac{AE}{AD}\)=\(\dfrac{AC}{AB}\)
    Xét tam giác ADE và tam giác ABC ta có :

                   góc A chung 
                   \(\dfrac{AE}{AD}\)=\(\dfrac{AC}{AB}\) (cmt)
       \(\Rightarrow\)tam giác ADE đồng dạng với tam giác ABC ( đpcm )

Đặt \(p^n+8=k^3\left(k\inℕ,k\ge3\right)\)

\(\Leftrightarrow k^3-8=p^n\)

\(\Leftrightarrow\left(k-2\right)\left(k^2+2k+4\right)=p^n\)

\(\Leftrightarrow k-2=p^i\left(i\inℕ,i\le n\right)\)

\(\Leftrightarrow k=p^i+2\)

Ta có \(p^n+8=k^3\)

\(\Leftrightarrow p^n+8=\left(p^i+2\right)^3\)

\(\Leftrightarrow p^n=p^{3i}+6p^{2i}+12p^i\) (*)

Đặt \(p^j=\dfrac{p^n}{p^i}\left(j\inℕ,j\le n\right)\), khi đó (*) thành 

\(p^j=p^{2i}+6p^{2i}+12\) (**)

Xét \(i=0\Leftrightarrow p^j=19\Leftrightarrow\left(p,j\right)=\left(19,1\right)\) \(\Rightarrow n=1\)

Ta tìm được một bộ \(\left(p,n\right)=\left(17,1\right)\)

Nếu \(j=0\) thì vô lí. Xét \(i,j\ge1\) . Khi đó ta có \(12⋮p\) \(\Rightarrow p\in\left\{2,3\right\}\)

Với \(p=2\), ta có \(2^n+8=k^3\) \(\Rightarrow k⋮2\Rightarrow k=2l\left(l\inℕ\right)\)

\(\Rightarrow2^n+8=8l^3\Leftrightarrow2^{n-3}+1=l^3\) \(\left(n\ge3\right)\)

\(\Leftrightarrow\left(l-1\right)\left(l^2+l+1\right)=2^{n-3}\)

\(\Leftrightarrow l-1=2^m\left(m\le n-3\right)\)

\(\Leftrightarrow l=2^m+1\)

Do đó \(2^{n-3}+1=\left(2^m+1\right)^3\) 

\(\Leftrightarrow2^{n-3}=2^{3m}+3.2^{2m}+3.2^m\)

\(\Leftrightarrow2^{n-3-m}=2^{2m}+3.2^m+3\)

\(\Rightarrow3⋮2^{n-3-m}\) \(\Leftrightarrow n-3-m=0\) \(\Leftrightarrow m=n-3\)

\(\Leftrightarrow l^2+l+1=1\) \(\Leftrightarrow l=0\) \(\Leftrightarrow k=0\), vô lí.

Với \(p=3\), ta có \(3^n+8=k^3\) \(\Rightarrow k\) chia 3 dư 2 \(\Rightarrow k=3q+2\left(q\inℕ^∗\right)\)

\(\Rightarrow3^n+8=\left(3q+2\right)^3\)

\(\Leftrightarrow3^n=27q^3+54q^2+36q\)

\(\Leftrightarrow3^{n-2}=q\left(3q^2+6q+4\right)\) \(\left(n\ge2\right)\)

 Dễ thấy nếu \(n=2\) thì vô lí. Xét \(n\ge3\). Khi đó vì \(3q^2+6q+4⋮̸3\) nên \(3q^2+6q+4=1\), vô lí.

Vậy \(\left(p,n\right)=\left(19,1\right)\) là cặp số duy nhất thỏa mãn ycbt.

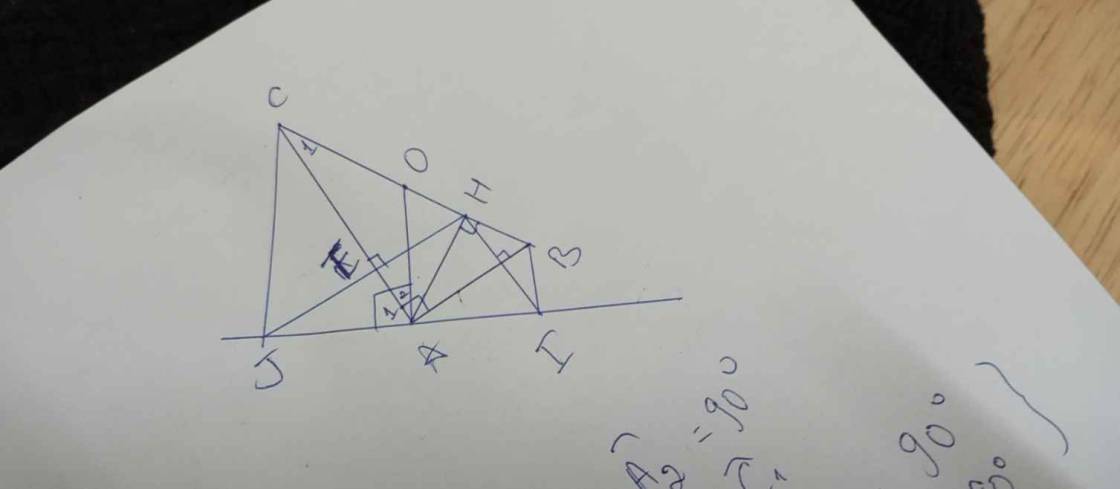
Câu e:

$\widehat {A_1}+\widehat{A_2}=90^{\circ}$

$\widehat{A_2}=\widehat{C_1}$

$\Rightarrow \widehat{A_1}+\widehat{C_1}=90^{\circ}$

Mặt khác $\widehat{C_1}+\widehat{CAH} = 90^{\circ}$

Suy ra $A_1=\widehat{CAH}$ (1)

Chứng minh được $\Delta JAE = \Delta HAE$ (cgv-gn)

$\Rightarrow AJ=AH$ (2)

Từ (1); (2) và chung cạnh $AC$ ta suy ra $\Delta AJC=\Delta AHC$ (c.g.c).

Suy ra $\widehat {J}=90^{\circ}$ hay $CJ\bot IJ$.

Chứng minh tương tự $BI \bot IJ$.

Bài 4:

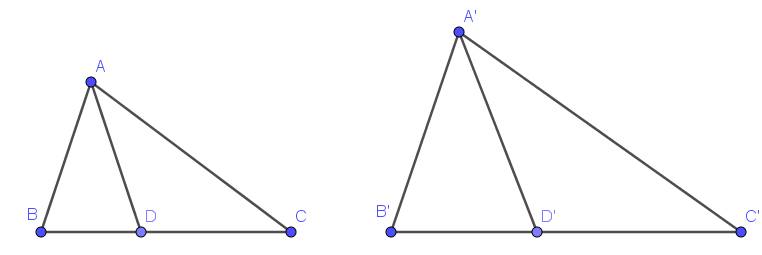
a. Vì $\triangle ABC\sim \triangle A'B'C'$ nên:

$\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}(1)$ và $\widehat{ABC}=\widehat{A'B'C'}$

$\frac{DB}{DC}=\frac{D'B'}{D'C}$

$\Rightarrow \frac{BD}{BC}=\frac{D'B'}{B'C'}$

$\Rightarrow \frac{BD}{B'D'}=\frac{BC}{B'C'}(2)$

Từ $(1); (2)\Rightarrow \frac{BD}{B'D'}=\frac{BC}{B'C'}=\frac{AB}{A'B'}$

Xét tam giác $ABD$ và $A'B'D'$ có:

$\widehat{ABD}=\widehat{ABC}=\widehat{A'B'C'}=\widehat{A'B'D'}$

$\frac{AB}{A'B'}=\frac{BD}{B'D'}$

$\Rightarrow \triangle ABD\sim \triangle A'B'D'$ (c.g.c)

b.

Từ tam giác đồng dạng phần a và (1) suy ra:
$\frac{AD}{A'D'}=\frac{AB}{A'B'}=\frac{BC}{B'C'}$

$\Rightarrow AD.B'C'=BC.A'D'$

Hình bài 4:

Đề lỗi rồi bạn. Bạn xem lại nhé.

Lời giải:

ĐKXĐ: $x\neq \pm 2; x\neq 0$

\(A=\left[\frac{3x^2+4}{x(x+2)}+\frac{x(2x-4)}{x(x+2)}\right].\frac{2x}{(x-2)(x+2)}\\ =\frac{3x^2+4+2x^2-4x}{x(x+2)}.\frac{2x}{(x-2)(x+2)}\\ =\frac{5x^2-4x+4}{x(x+2)}.\frac{2x}{(x-2)(x+2)}\\ =\frac{2(5x^2-4x+4)}{(x-2)(x+2)^2}\)

Biểu thức sau khi thu gọn xấu quá bạn. Bạn có viết sai đề không nhỉ?

Ta có: DE//AC (cùng vuông góc với AB) 

Áp dụng định lý Ta-lét ta có:

\(\dfrac{BD}{AD}=\dfrac{BE}{CE}\Rightarrow\dfrac{BD}{AD}=\dfrac{BE}{BC-BE}\Rightarrow\dfrac{6}{x}=\dfrac{3x}{13,5-3x}\)

\(\Leftrightarrow6\left(13,5-3x\right)=x\cdot3x\)

\(\Leftrightarrow81-18x=3x^2\)

\(\Leftrightarrow27-6x=x^2\)

\(\Leftrightarrow x^2+6x-27=0\)

\(\Leftrightarrow x^2-3x+9x-27=0\)

\(\Leftrightarrow x\left(x-3\right)+9\left(x-3\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x+9\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-9\left(ktm\right)\end{matrix}\right.\)

Vậy: `x=3`