\(\dfrac{x+3}{15}\)=\(\dfrac{1}{3}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số cần tìm có dạng là \(\overline{ab}\)
Chữ số hàng chục lớn hơn chữ số hàng đơn vị là 6 đơn vị nên a-b=6
Nếu đổi chỗ hai chữ số cho nhau thì tổng của số mới và số cũ là 132 nên \(\overline{ab}+\overline{ba}=132\)
=>10a+b+10b+a=132
=>11a+11b=132
=>a+b=12
mà a-b=6
nên \(a=\dfrac{12+6}{2}=9;b=12-9=3\)
Vậy: Số cần tìm là 93

\(c,125\ge5^{n+1}>25\\ =>5^3\ge5^{n+1}>5^2\\ =>3\ge n+1>2\\ =>3-1\ge n>2-1\\ =>2\ge n>1\)
Mà n là số tự nhiên
=> n = 2
\(d,2\cdot16\ge2^n>4\\ =>2\cdot2^4\ge2^n>2^2\\ =>2^{1+4}\ge2^n>2^2\\ =>2^5\ge2^n>2^2\\ =>5\ge n>2\)
Mà n là số tự nhiên
=> n ∈ {3; 4; 5}

Chiều rộng của căn phòng là:
`1/3 xx 12 = 4(m)`
Diện tích căn phòng là:
`12 x 4 = 48(m^2)`
Đổi: 8dm = 0,8m
Diện tích viên gạch là:
`0,8 xx 0,8 = 0,64(m^2)`
Số viên gạch cần dùng là:
`48:0,64=75` (viên)
ĐS: ...

\(\left(a-x\right)y^3-\left(a-y\right)x^3+\left(x-y\right)a^3\\ =ay^3-xy^3-ax^3+x^3y+a^3x-a^3y\\ =\left(ay^3-ax^3\right)+\left(-xy^3+xy^3\right)+\left(a^3x-a^3y\right)\\ =a\left(y^3-x^3\right)+-xy\left(y^2-x^2\right)+a^3\left(x-y\right)\\ =a\left(y-x\right)\left(x^2+xy+y^2\right)-xy\left(y-x\right)\left(x+y\right)-a^3\left(y-x\right)\\ =\left(y-x\right)\left[a\left(x^2+xy+y^2\right)-xy\left(x+y\right)-a^3\right]\\ =\left(y-x\right)\left(ax^2+axy+ay^2-x^2y-xy^2-a^3\right)\)

\(125>5^{n+1}>25\\ \Rightarrow5^3>5^{n+1}>5^2\\ \Rightarrow3>n+1>2\\ \Rightarrow3-1>n>2-1\\ \Rightarrow2>n>1\)
Mà giữa 2 và 3 không có số tự nhiên nào
=> Không có n thỏa mãn

\(x^3-5x^2+8x-4\\ =\left(x^3-x^2\right)+\left(-4x^2+4x\right)+\left(4x-4\right)\\ =x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)\\ =\left(x^2-4x+4\right)\left(x-1\right)\\ =\left[x^2-2\cdot x\cdot2+2^2\right]\left(x-1\right)\\ =\left(x-2\right)^2\left(x-1\right)\)

a: Ta có: BH\(\perp\)AC
CK\(\perp\)AC
Do đó: BH//CK
Ta có: CH\(\perp\)AB
BK\(\perp\)BA
Do đó: CH//BK
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
b: BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
=>H,M,K thẳng hàng
c: Xét ΔHIK có
G,M lần lượt là trung điểm của HI,HK
=>GM là đường trung bình của ΔHIK
=>GM//IK
=>BC//IK
Xét ΔCHI có
CG là đường cao
CG là đường trung tuyến
Do đó: ΔCHI cân tại C
=>CH=CI
mà CH=BK
nên BK=CI
Xét tứ giác BCKI có BC//KI và BK=CI
nên BCKI là hình thang cân

\(x^3-x^2-14x+24\\ =\left(x^3-2x^2\right)+\left(x^2-2x\right)+\left(-12x+24\right)\\ =x^2\left(x-2\right)+x\left(x-2\right)-12\left(x-2\right)\\ =\left(x-2\right)\left(x^2+x-12\right)\\ =\left(x-2\right)\left[\left(x^2-3x\right)+\left(4x-12\right)\right]\\ =\left(x-2\right)\left[x\left(x-3\right)+4\left(x-3\right)\right]\\ =\left(x-2\right)\left(x-3\right)\left(x+4\right)\)

\(a,M=\left(x+1\right)^3-x^3+1-3x\left(x+1\right)\\ =x^3+3x^2+3x+1-x^3+1-3x^2-3x\\ =\left(x^3-x^3\right)+\left(3x^2-3x^2\right)+\left(3x-3x\right)+\left(1+1\right)\\ =2\)
Vậy giá trị của bt không phụ thuộc vào biến
\(b,\left(2x-1\right)^3-6x\left(2x-1\right)^2+12x^2\left(2x-1\right)-8x^3\\ =\left(2x-1\right)^3-3\cdot\left(2x-1\right)^2\cdot2x+3\cdot\left(2x-1\right)\cdot\left(2x\right)^2-\left(2x\right)^3\\ =\left(2x-1-2x\right)^3\\ =\left(-1\right)^3=-1\)
Vậy giá trị của bt không phụ thuộc vào biến
\(c,P=\left(x+y+1\right)^3-\left(x+y-1\right)^3-6\left(x+y\right)^2\\ =\left(x+y+1-x-y+1\right)\left[\left(x+y+1\right)^2+\left(x+y+1\right)\left(x+y-1\right)+\left(x+y-1\right)^2\right]-6\left(x+y\right)^2\\ =2\left[\left(x+y\right)^2+2\left(x+1\right)+1+\left(x+y\right)^2-1+\left(x+y\right)^2-2\left(x+y\right)+1\right]-6\left(x+y\right)^2\\ =2\left[3\left(x+y\right)^2+1\right]-6\left(x+y\right)^2\\ =6\left(x+y\right)^2+2-6\left(x+y\right)^2\\ =2\)
Vậy giá trị của bt không phụ thuộc vào biến

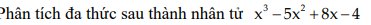



\(\dfrac{x+3}{15}=\dfrac{1}{3}\\ \dfrac{x+3}{15}=\dfrac{5}{15}\\ x+3=5\\ x=5-3\\ x=2\)
Vậy x = 2
\(\dfrac{x+3}{15}=\dfrac{1}{3}\)
\(\Rightarrow x+3:15=\dfrac{1}{3}\)
\(\Rightarrow x+\dfrac{1}{5}=\dfrac{1}{3}\)
\(\Rightarrow x=\dfrac{1}{3}-\dfrac{1}{5}\)
\(\Rightarrow x=\dfrac{2}{15}\)