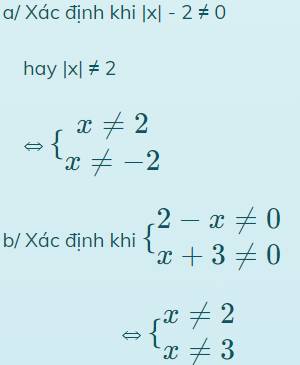
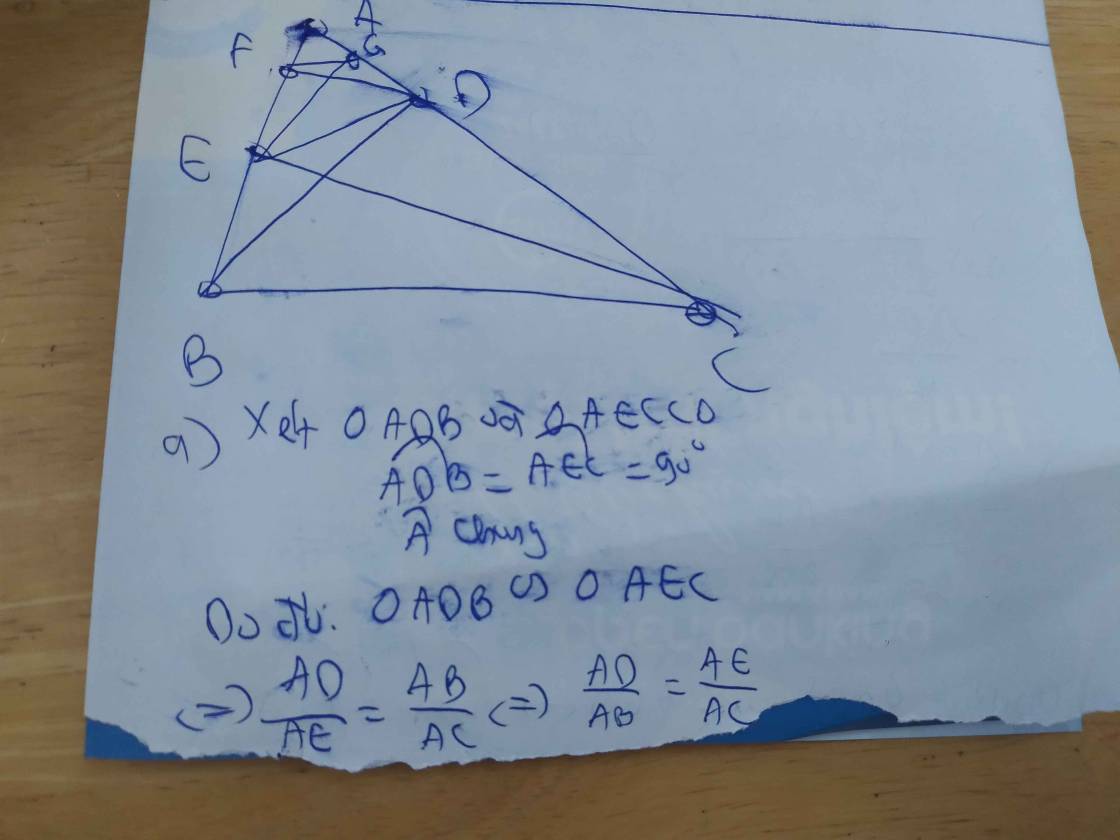
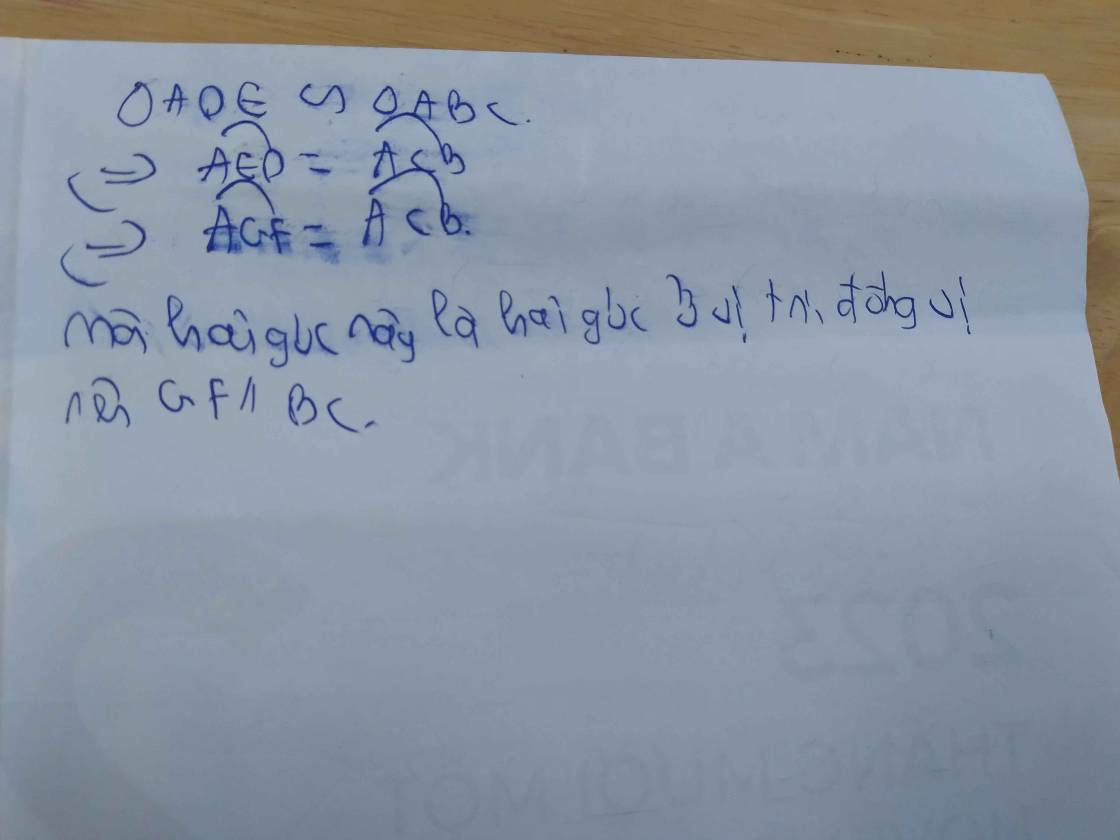
a: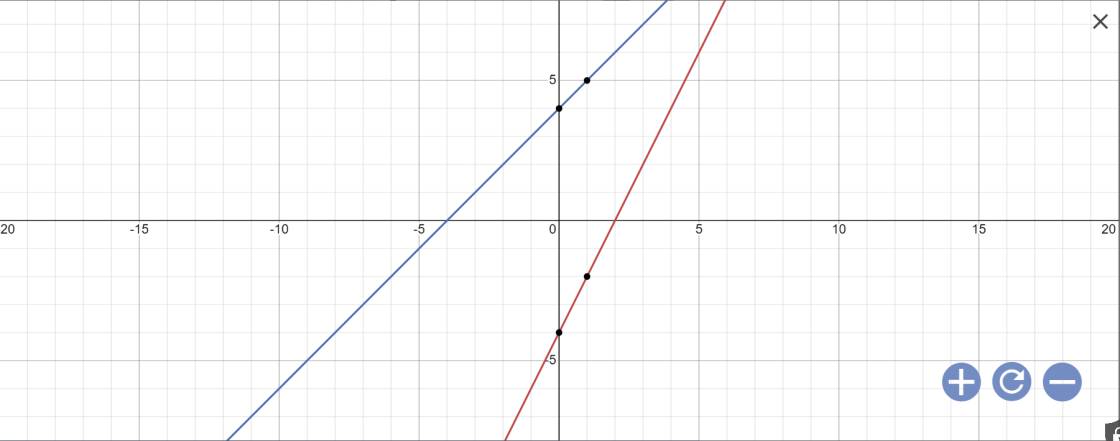 

b: Phương trình hoành độ giao điểm là:

2x-4=x+4

=>2x-x=4+4

=>x=8

Thay x=8 vào y=x+4, ta được:

y=8+4=12

Vậy: Q(8;12)

Tọa độ N là:

\(\left\{{}\begin{matrix}x=0\\y=2\cdot0-4=-4\end{matrix}\right.\)

Vậy: N(0;-4)

Tọa độ M là:

\(\left\{{}\begin{matrix}x=0\\y=0+4=4\end{matrix}\right.\)

Vậy: M(0;4)

M(0;4); N(0;-4); Q(8;12)

\(MN=\sqrt{\left(0-0\right)^2+\left(-4-4\right)^2}=8\)

\(MQ=\sqrt{\left(8-0\right)^2+\left(12-4\right)^2}=\sqrt{8^2+8^2}=8\sqrt{2}\)

\(NQ=\sqrt{\left(8-0\right)^2+\left(12+4\right)^2}=\sqrt{8^2+16^2}=8\sqrt{5}\)

Xét ΔMNQ có \(cosMNQ=\dfrac{NM^2+NQ^2-MQ^2}{2\cdot NM\cdot NQ}=\dfrac{256}{2\cdot8\cdot8\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)

=>\(sinMNQ=\sqrt{1-\left(\dfrac{2}{\sqrt{5}}\right)^2}=\dfrac{1}{\sqrt{5}}\)

Diện tích ΔMNQ là:

\(S_{MNQ}=\dfrac{1}{2}\cdot NM\cdot NQ\cdot sinMNQ\)

\(=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{5}}\cdot8\cdot8\sqrt{5}=\dfrac{64}{2}=32\)

a: Để \(f\left(x\right)=\dfrac{2}{\left|x\right|-2}\) có nghĩa thì \(\left|x\right|-2\ne0\)

=>\(\left|x\right|\ne2\)

=>\(x\in R\backslash\left\{2;-2\right\}\)

b: Để \(f\left(x\right)=\dfrac{1}{2-x}+\dfrac{1}{x+3}\) có nghĩa thì \(\left\{{}\begin{matrix}2-x\ne0\\x+3\ne0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x\ne2\\x\ne-3\end{matrix}\right.\)

Xét tg BCD có

AI//BC (gt)\(\Rightarrow\dfrac{BM}{DM}=\dfrac{CI}{DI}\) (Talet) (1)

KP//BD (gt) \(\Rightarrow\dfrac{BP}{CP}=\dfrac{DK}{CK}\) (Talet) (2)

Xét tứ giác ABKD có

AB//CD (gt) => AB//DK

KP//AD (gt) 

=> ABKD là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => AB=DK (cạnh đối hbh) (3)

Xét tứ giác ABCI có

AB//CD (gt) => AB//CI

AI//BC

=> ABCI là hbh => AB=CI (cạnh đối hbh) (4)

Từ (3) và (4) => CI=DK (5)

Ta có

IK=DK-DI

IK=CI-CK

Mà CI=DK (cmt)

=> DI=CK (6)

Từ (1) (2) (5) (6) \(\Rightarrow\dfrac{BM}{DM}=\dfrac{BP}{CP}\)

Xét tg BCD có

\(\dfrac{BM}{DM}=\dfrac{BP}{CP}\) (cmt) => MP//DC (Talet đảo)

a: ta có: \(AM=MB=\dfrac{AB}{2}\)

\(BN=NC=\dfrac{BC}{2}\)

mà AB=BC

nên AM=MB=BN=NC

Xét ΔMBC vuông tại B và ΔNCD vuông tại C có

MB=NC

BC=CD

Do đó: ΔMBC=ΔNCD

=>\(\widehat{MCB}=\widehat{NDC}\)

mà \(\widehat{NDC}+\widehat{DNC}=90^0\)(ΔNCD vuông tại C)

nên \(\widehat{MCB}+\widehat{DNC}=90^0\)

=>CM\(\perp\)DN tại I

=>ΔCIN vuông tại I

b: \(CN=\dfrac{CB}{2}=\dfrac{a}{2}\)

ΔNCD vuông tại C

=>\(DC^2+CN^2=DN^2\)

=>\(DN^2=\dfrac{a^2}{4}+a^2=\dfrac{5}{4}a^2\)

=>\(DN=\dfrac{a\sqrt{5}}{2}\)

Ta có: ΔNCD vuông tại C

=>\(S_{CND}=\dfrac{1}{2}\cdot CD\cdot CN=\dfrac{1}{2}\cdot a\cdot\dfrac{a}{2}=\dfrac{a^2}{4}\)

Xét ΔNCD vuông tại C và ΔNIC vuông tại I có

\(\widehat{CND}\) chung

Do đó: ΔNCD~ΔNIC

=>\(\dfrac{S_{NCD}}{S_{NIC}}=\dfrac{ND}{NC}=\dfrac{a\sqrt{5}}{2}:\dfrac{a}{2}=\sqrt{5}\)

=>\(S_{NIC}=\dfrac{a^2}{4\sqrt{5}}\)

a/

Ta có

\(AD\perp BC\left(gt\right),OM\perp BC\) => AH//OM (cung vuông góc với BC)

\(BE\perp AC\left(gt\right);ON\perp AC\) => BE//ON (cùng vuông góc với AC)

\(\Rightarrow\widehat{MON}=\widehat{AHB}\) (góc có cạnh tương ứng //) (1)

Ta có

MB=MC(gt); NA=NC(gt) => MN là đường trung bình của tg ABC

=> MN//AB

ON//BE (cmt)

\(\Rightarrow\widehat{ONM}=\widehat{HBA}\) (góc có cạnh tương ứng //) (2)

Từ (1) và (2) => tg OMN đồng dạng với tg HAB (g.g.g)

b/

Nối G với O và nối G với H

Nối O với H cắt BN tại G'

Ta có

MN là đường trung bình của tg ABC \(\Rightarrow MN=\dfrac{AB}{2}\Rightarrow\dfrac{MN}{AB}=\dfrac{1}{2}\)

tg OMN đồng dạng với tg HAB

\(\Rightarrow\dfrac{ON}{BH}=\dfrac{MN}{AB}=\dfrac{1}{2}\)

Ta có

ON//BE (cmt) \(\Rightarrow\dfrac{G'N}{G'B}=\dfrac{ON}{BH}=\dfrac{1}{2}\) (Talet)

Mà do G là trọng tâm của tg ABC \(\Rightarrow\dfrac{GN}{GB}=\dfrac{1}{2}\)

\(\Rightarrow G'\equiv G\) Hay nói cách khác là O; G; H thẳng hàng

Xét tg GOM và tg GHA có

\(\widehat{OGM}=\widehat{HGA}\) (góc đối đỉnh)

AD//OM (cmt) \(\Rightarrow\widehat{GMO}=\widehat{GAH}\) (góc so le trong)

=> tg GOM đồng dạng với tg GHA

c/ Ba điểm O, G, H thẳng hàng đã c/m ở trên

Ta có

BE//ON (cmt) \(\Rightarrow\dfrac{OG}{GH}=\dfrac{ON}{BH}=\dfrac{1}{2}\left(Talet\right)\)

\(\Rightarrow GH=2OG\)

a/

Ta có

\(\widehat{MBC}+\widehat{CBN}=\widehat{MBN}=90^o\)

Xét tg NBC có

NC=NB (gt) => tg NBC cân tại N \(\Rightarrow\widehat{CBN}=\widehat{BCN}\)

\(\Rightarrow\widehat{MBC}+\widehat{CBN}=\widehat{MBC}+\widehat{BCN}=90^o\) (1)

Ta có

\(\widehat{ABN}+\widehat{ABM}=\widehat{MBN}=90^o\)

\(\widehat{ABM}=\widehat{BAM}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{ABN}+\widehat{ABM}=\widehat{ABN}+\widehat{BAM}=90^o\) (2)

Cộng 2 vế của (1) với (2) ta có

\(\widehat{MBC}+\widehat{BCN}+\widehat{ABN}+\widehat{BAM}=90^o+90^o=180^o\)

Xét tg ABC có

\(180^0-\widehat{ABC}=\left(\widehat{BCN}+\widehat{BAM}\right)\)

\(\Rightarrow\widehat{MBC}+\widehat{ABN}+180^o-\widehat{ABC}=180^o\)

\(\Rightarrow\widehat{MBC}+\widehat{ABN}=\widehat{ABC}\)

Mà 

\(\widehat{MBC}+\widehat{ABN}+\widehat{ABC}=\widehat{MBN}=90^o\)

\(\Rightarrow\widehat{ABC}+\widehat{ABC}=90^o\Rightarrow\widehat{ABC}=45^o\)

b/

Từ N dựng đt vuông góc với BD ta có

tg NBC cân tại N (cmt) 

\(\Rightarrow\widehat{HNC}=\widehat{HNB}\) (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh) (3)

Xét tg vuông MCD có

\(\widehat{MDC}+\widehat{MCD}=90^o\)

Xét tg vuông HNC có

\(\widehat{HNC}+\widehat{HCN}=90^o\)

Mà \(\widehat{MCD}=\widehat{HCN}\) (góc đối đỉnh)

\(\Rightarrow\widehat{MDC}=\widehat{HNC}\) (4)

Ta có

\(NH\perp BD;NB\perp BM\Rightarrow\widehat{HNB}=\widehat{MBD}\) (Góc có cạnh tương ứng vuông góc) (5)

Từ (3) (4) (5) \(\Rightarrow\widehat{MDC}=\widehat{MBD}\) => tg MBD cân tại M => MB=MD

Mà tg MAB cân => MB=MA

=> MD=MA => tg MAD vuông cân tại M

Xét tg vuông MAD có

\(AD=\sqrt{MD^2+MA^2}=\sqrt{MD^2+MD^2}=\sqrt{2}.MD\)

Xét ΔABC có AD là phân giác

nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)\)

=>\(3=\dfrac{2\cdot\sqrt{3}\cdot AC}{\sqrt{3}+AC}\cdot cos45\)

=>\(3=\dfrac{2\sqrt{3}\cdot AC}{AC+\sqrt{3}}\cdot\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{6}\cdot AC}{AC+\sqrt{3}}\)

=>\(3AC+3\sqrt{3}=\sqrt{6}\cdot AC\)

=>\(\left(3-\sqrt{6}\right)\cdot AC=-3\sqrt{3}\)

=>\(AC=\dfrac{-3\sqrt{3}}{3-\sqrt{6}}< 0\)

=>Không có tam giác ABC nào thỏa mãn dữ kiện đề bài

=>Ko tính được góc ADB

\(E=2\left(x^2+4xy+4y^2\right)+3y^2-4x-2y+6\)

\(=2\left(x+2y\right)^2-4\left(x+2y\right)+2+3y^2+6y+3+1\)

\(=2\left(x+2y-1\right)^2+3\left(y+1\right)^2+1\ge1\)

\(E_{min}=1\) khi \(\left\{{}\begin{matrix}x+2y-1=0\\y+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)

a) Áp dụng tính chất đường phân giác trong tam giác ABM, ta có:

\(\dfrac{DA}{DB}=\dfrac{MA}{MB}\)

 Tương tự, ta có \(\dfrac{EA}{EC}=\dfrac{MA}{MC}\)

 Nhưng vì AM là trung tuyến của tam giác ABC \(\Rightarrow MB=MC\)  nên ta có \(\dfrac{DA}{DB}=\dfrac{EA}{EC}\) . Áp dụng định lý Thales đảo \(\Rightarrow\) DE//BC (đpcm)

 b) Áp dụng định lý Thales cho tam giác ABM, ta có:

 \(\dfrac{AI}{AM}=\dfrac{DI}{BM}\) 

 Tương tự, ta có \(\dfrac{AI}{AM}=\dfrac{EI}{CM}\)

 Do đó: \(\dfrac{DI}{BM}=\dfrac{EI}{CM}\)

 Mà \(BM=CM\Rightarrow EI=DI\) \(\Rightarrow\) I là trung điểm DE (đpcm)