giải phương trình\(\sqrt{x^2+x+9}=2x-4+\sqrt{x+1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Công thức cấu tạo của axit 4-cloromecuribenzoic là:
C O OH Hg CI
(Đây là công thức cấu tạo thu gọn)
Công thức phân tử: \(ClHgC_6H_4COOH\)
~HT~

mình nghĩ pt (P) : y = ax^2 - bx + c chứ ?
a, (P) đi qua điểm A(0;-1) <=> \(c=-1\)
(P) đi qua điểm B(1;-1) <=> \(a-b+c=-1\)(1)
(P) đi qua điểm C(-1;1) <=> \(a+b+c=1\)(2)
Thay c = -1 vào (1) ; (2) ta được : \(a-b=0;a+b=2\Rightarrow a=1;b=1\)
Vậy pt Parabol có dạng \(x^2-x-1=y\)
Bài 1b
(P) đi qua điểm A(8;0) <=> \(64a-8b+c=0\)
(P) có đỉnh I(6;12) \(\Rightarrow\hept{\begin{cases}-\frac{b}{2a}=6\\36a-6b+c=-12\end{cases}}\Rightarrow a=3;b=-36;c=96\)
Vậy pt Parabol có dạng : \(9x^2+36x+96=y\)
tương tự nhé



xin lỗi mình nhầm nhe các bạn !
phải là x\(\inℤ\) mới đúng 😓😓

câu 1.
\(2x^2-x-6=0\Leftrightarrow\left(x-2\right)\left(2x+3\right)=0\Leftrightarrow\orbr{\begin{cases}x=2\\x=-\frac{3}{2}\end{cases}}\)
b.\(\frac{2}{x+2}=\frac{1}{2x+1}\Rightarrow2\left(2x+1\right)=x+2\Leftrightarrow3x=0\Leftrightarrow x=0\)
thay lại thấy thỏa mãn vậy pt có nghiệm x=0
.bài 4
\(d:5\left(x+2\right)+1\left(y-3\right)=0\text{ hay }5x+y+7=0\)
bài 5.
Tâm I(2,-3) bán kính 4

1. Định lí Pytago
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
ΔABC vuông tại A thì ta có:
AB2+AC2=BC2
a2+b2=c2



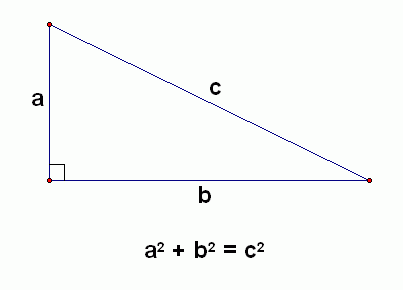
tttttttttttttttttttt
\(ĐK:X\ge-1\)
xét x = -1 ta có \(\sqrt{\left(-1\right)^2+1+9}=2\left(-1\right)-4+\sqrt{-1+1}\)
\(\Leftrightarrow\sqrt{11}=-6\left(voli\right)\)
=> x = - 1 không là nghiệm của pt
=> x > -1
=> x + 1 > 0
chia cả 2 vế cho \(\sqrt{x+1}\) ta được :
\(\sqrt{\frac{x^2+x+9}{x+1}}=\frac{2\left(x-2\right)}{\sqrt{x+1}}+1\)
\(\Leftrightarrow\sqrt{\frac{x^2-4x+4+5x+5}{x+1}}=2\cdot\frac{x-2}{\sqrt{x+1}}+1\)
\(\Leftrightarrow\sqrt{\frac{\left(x-2\right)^2}{x+1}+5}=2\cdot\frac{x-2}{\sqrt{x+1}}+1\)
\(\Leftrightarrow\sqrt{\left(\frac{x-2}{\sqrt{x+1}}\right)^2+5}=2\cdot\frac{x-2}{\sqrt{x+1}}+1\)
đặt \(\frac{x-2}{\sqrt{x+1}}=t\) ta có
\(\sqrt{t^2+5}=2t+1\left(đk:t\ge-\frac{1}{2}\right)\)
\(\Leftrightarrow t^2+5=4t^2+4t+1\)
\(\Leftrightarrow3t^2+4t-4=0\)
\(\Leftrightarrow\orbr{\begin{cases}t=\frac{2}{3}\left(tm\right)\\t=-2\left(loai\right)\end{cases}}\)
t = 2/3 => \(\frac{x-2}{\sqrt{x+1}}=\frac{2}{3}\Leftrightarrow3x-6=2\sqrt{x+1}\) (đk x >= 2)
\(\Rightarrow9x^2-36x+36=4x+4\)
\(\Leftrightarrow9x^2-40x+32=0\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{20-4\sqrt{7}}{9}\left(loai\right)\\x=\frac{20+4\sqrt{7}}{9}\left(tm\right)\end{cases}}\)
vậy x = ...