 giúp em bài 3 và ý c bài 2 ạ
giúp em bài 3 và ý c bài 2 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)(hai góc so le trong, AD//CB)
Do đó: ΔAHD=ΔCKB
=>AH=CK
Ta có: AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó:AHCK là hình bình hành
b: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
ta có: AHCK là hình bình hành
=>AC cắt HK tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của HK
c: Xét tứ giác AMCN có
AM//CN
AN//CM
Do đó: AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN
=>M,O,N thẳng hàng



Bài 4:
a: \(216x^3+27y^3=27\left(8x^3+y^3\right)\)
\(=27\left[\left(2x\right)^3+y^3\right]\)
\(=27\left(2x+y\right)\left(4x^2-2xy+y^2\right)\)
b: \(64a^3-8=8\left(8a^3-1\right)\)
\(=8\left[\left(2a\right)^3-1^3\right]\)
\(=8\left(2a-1\right)\left(4a^2+2a+1\right)\)
c: \(x^3+8=x^3+2^3=\left(x+2\right)\left(x^2-2x+4\right)\)
d: \(27x^3-8y^3=\left(3x\right)^3-\left(2y\right)^3\)
\(=\left(3x-2y\right)\left[\left(3x\right)^2+3x\cdot2y+\left(2y\right)^2\right]\)
\(=\left(3x-2y\right)\left(9x^2+6xy+4y^2\right)\)
Bài 5:
a: \(3\left(x-y\right)^2-2\left(x+y\right)^2-\left(x-y\right)\left(x+y\right)\)
\(=3\left(x^2-2xy+y^2\right)-2\left(x^2+2xy+y^2\right)-\left(x^2-y^2\right)\)
\(=3x^2-6xy+3y^2-2x^2-4xy-2y^2-x^2+y^2\)
\(=2y^2-10xy\)
b: \(\left(x-y\right)^3-3\left(x-y\right)^2\cdot x+3\left(x-y\right)\cdot x^2-x^3\)
\(=\left(x-y-x\right)^3\)
\(=\left(-y\right)^3=-y^3\)
c: \(\left(3x+3\right)^3-2\left(x+1\right)^3-\left(5x-1\right)^2\)
\(=27\left(x+1\right)^3-2\left(x+1\right)^3-\left(5x-1\right)^2\)
\(=25\left(x+1\right)^3-25x^2+10x-1\)
\(=25x^3+75x^2+75x+25-25x^2+10x-1\)
\(=25x^3+50x^2+85x+24\)
d: \(\left(-2x+3\right)^3-\left(x+1\right)^3+\left(3x-1\right)^2\)
\(=\left(-2x+3-x-1\right)\left[\left(-2x+3\right)^2+\left(-2x+3\right)\left(x+1\right)+\left(x+1\right)^2\right]+\left(3x-1\right)^2\)
\(=\left(-3x+2\right)\left(4x^2-12x+9-2x^2+x+3+x^2+2x+1\right)+\left(3x-1\right)^2\)
\(=\left(-3x+2\right)\left(3x^2-9x+13\right)+\left(3x-1\right)^2\)
\(=-9x^3+27x^2-39x+6x^2-18x+26+9x^2-6x+1\)
\(=-9x^3+42x^2-63x+27\)


a: Ta có: \(\widehat{OMN}=\widehat{MQP}\)(hai góc đồng vị, MN//PQ)
\(\widehat{ONM}=\widehat{NPQ}\)(hai góc đồng vị, MN//PQ)
mà \(\widehat{MQP}=\widehat{NPQ}\)(MNPQ là hình thang cân)
nên \(\widehat{OMN}=\widehat{ONM}\)
=>ΔOMN cân tại O
b: Xét ΔMNQ và ΔNMP có
NM chung
NQ=MP
MQ=NP
Do đó: ΔMNQ=ΔNMP
c: H ở đâu vậy bạn?

\(x^2-10x-11=0\)
=>\(x^2-10x+25-36=0\)
=>\(\left(x-5\right)^2-6^2=0\)
=>(x-5-6)(x-5+6)=0
=>(x-11)(x+1)=0
=>\(\left[{}\begin{matrix}x-11=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-1\end{matrix}\right.\)
\(x^2\)\(-2.x.5+5^2\)\(-36\)\(=0\)
\(\Leftrightarrow\)\(\left(x-5\right)^2\)\(-36=0\)
\(\Leftrightarrow\left(x-5^{ }\right)^2\)\(=36\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=6\\x-5=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-1\end{matrix}\right.\)

a: \(\left(3x+4y\right)^2+\left(4x-3y\right)^2\)
\(=9x^2+24xy+16y^2+16x^2-24xy+9y^2\)
\(=25x^2+25y^2\)
b: \(\left(x^2+6x+9\right)-\left(25x^2-40x+16\right)\)
\(=x^2+6x+9-25x^2+40x-16\)
\(=-24x^2+46x-7\)
a, ( 3x +4y)^2 + ( 4x-3y)^2
= ( 3x + 4y )^2 - ( 3y - 4x )^2 ( hằng đẳng thức số 2)
b, (x^2 +6x+9)-(25x^2-40x+16)
= (x^2 +3x +3x +9) - (25x^2 - 20x - 20x +16)
= [(x^2 + 3x) + (3x + 9 )] - [(25x^2 -20x)+(-20x+16)]
= [x(x+3)+3(x+3)] - [5x(5x-4)-4(5x-4)]
= (x+3)(x+3) - (5x-4)(5x-4)
= (x+3)^2 - (5x-4)^2 ( hằng đẳng thức số 2)

f(2)=0
=>\(a\cdot2^2+b\cdot2+c=0\)
=>4a+2b+c=0
=>c=-4a-2b
=>\(f\left(x\right)=ax^2+bx-4a-2b\)
\(=a\left(x^2-4\right)+b\left(x-2\right)\)
\(=a\left(x-2\right)\left(x+2\right)+b\left(x-2\right)\)
\(=\left(x-2\right)\left(ax+2a+b\right)⋮x-2\)
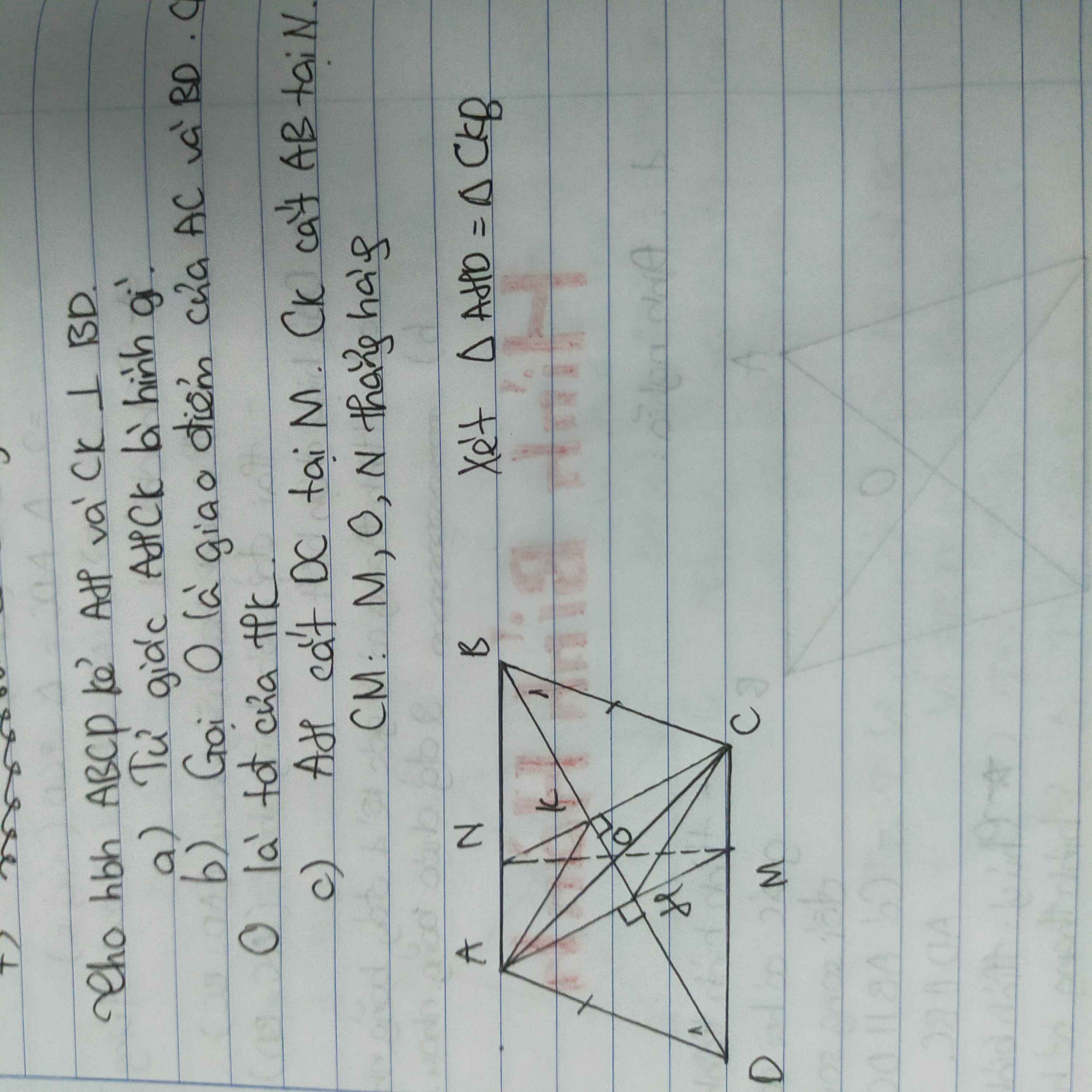



Bài 2:
c: \(C=27x^3-27x^2y+9xy^2-y^3-121\)
\(=\left(3x\right)^3-3\cdot\left(3x\right)^2\cdot y+3\cdot3x\cdot y^2-y^3-121\)
\(=\left(3x-y\right)^3-121=7^3-121=343-121=222\)
Bài 3:
a: \(x^2-4+\left(x-2\right)^2\)
\(=\left(x-2\right)\left(x+2\right)+\left(x-2\right)^2\)
=(x-2)(x+2+x-2)
=2x(x-2)
b: \(x^3-2x^2+x-xy^2\)
\(=x\left(x^2-2x+1-y^2\right)\)
\(=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-1-y\right)\left(x-1+y\right)\)
c: \(x^3-4x^2-12x+27\)
\(=\left(x^3+27\right)-4x\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2-3x+9\right)-4x\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2-7x+9\right)\)
d: \(\left(x^2+x\right)^2-2\left(x^2+x\right)-15\)
\(=\left(x^2+x\right)^2-5\left(x^2+x\right)+3\left(x^2+x\right)-15\)
\(=\left(x^2+x\right)\left(x^2+x-5\right)+3\left(x^2+x-5\right)\)
\(=\left(x^2+x-5\right)\left(x^2+x+3\right)\)