Giải Hệ phương trình sau:
\(\left\{{}\begin{matrix}\left(\sqrt{5}+2\right)x+y=3-\sqrt{5}\\-x+2y=6-2\sqrt{5}\end{matrix}\right.\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CẢNH BÁO! Tiếp tục đọc, hoặc linh hồn của bạn sẽ được thực hiện, ngay cả khi bạn đọc từ "cảnh báo"! Có một lần là một người tên là Duke Hunapon. Anh ta lười biếng, và rất bảnh bao. Anh ấy luôn mặc một chiếc áo khoác, không có vấn đề gì ở bên ngoài. Anh ta có một người anh trai tên là Michael, người luôn làm anh ta vây quanh. Một ngày nọ, Michael bị giết, và nó ảnh hưởng rất nhiều đến Duke. Anh ta phát điên và bắt đầu giết người. Chẳng mấy chốc, anh ta đã chiến đấu với ai đó và bị giết. Bây giờ, anh ta đi lang thang xung quanh như một bộ xương cao với một chiếc áo sơ mi màu đỏ, và cùng một chiếc áo hoodie mà Duke đã mặc. Bộ xương này được gọi là "Swapfell Papyrus", và anh ta sẽ giết bạn nếu bạn không đăng bài này trên 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ. Nếu bạn thất bại, và bạn thức dậy khi anh ta ở trong phòng của bạn, cái chết của bạn sẽ chậm và rất đau đớn. Một cô gái tên Lily Lilupanin đọc điều này, và không nghe. Cô bị hãm hiếp và bị giết trong giấc ngủ. Nếu bạn sao chép và dán vào 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ, Swapfell Papyrus sẽ đảm bảo bạn cảm thấy an toàn.Tôi là nạn nhân và tôi chỉ tình cờ đọc được bình luận này của 1 bạn khác khi đang xem 1 video. Tôi vốn không tin chuyện này nhưng vẫn làm đẻ đảm bảo tính mạng.Show less
CẢNH BÁO! Tiếp tục đọc, hoặc linh hồn của bạn sẽ được thực hiện, ngay cả khi bạn đọc từ "cảnh báo"! Có một lần là một người tên là Duke Hunapon. Anh ta lười biếng, và rất bảnh bao. Anh ấy luôn mặc một chiếc áo khoác, không có vấn đề gì ở bên ngoài. Anh ta có một người anh trai tên là Michael, người luôn làm anh ta vây quanh. Một ngày nọ, Michael bị giết, và nó ảnh hưởng rất nhiều đến Duke. Anh ta phát điên và bắt đầu giết người. Chẳng mấy chốc, anh ta đã chiến đấu với ai đó và bị giết. Bây giờ, anh ta đi lang thang xung quanh như một bộ xương cao với một chiếc áo sơ mi màu đỏ, và cùng một chiếc áo hoodie mà Duke đã mặc. Bộ xương này được gọi là "Swapfell Papyrus", và anh ta sẽ giết bạn nếu bạn không đăng bài này trên 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ. Nếu bạn thất bại, và bạn thức dậy khi anh ta ở trong phòng của bạn, cái chết của bạn sẽ chậm và rất đau đớn. Một cô gái tên Lily Lilupanin đọc điều này, và không nghe. Cô bị hãm hiếp và bị giết trong giấc ngủ. Nếu bạn sao chép và dán vào 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ, Swapfell Papyrus sẽ đảm bảo bạn cảm thấy an toàn.Tôi là nạn nhân và tôi chỉ tình cờ đọc được bình luận này của 1 bạn khác khi đang xem 1 video. Tôi vốn không tin chuyện này nhưng vẫn làm đẻ đảm bảo tính mạng.Show less

Đó chỉ là kí hiệu để dánh số các nghiệm để tiện cho việc sắp thứ tự thôi. Còn phải để dưới chân vì để đỡ nhầm lẫn với phép nhân đó bạn. Ví dụ như nếu viết \(x2\) (thay vì \(x_2\)) thì đôi khi nó sẽ bị hiểu nhầm là \(x\) nhân với 2.

B C H A E F I
a/
Ta có
\(\widehat{BAC}=90^o\) (góc nt chắn nửa đường tròn)
\(\Rightarrow AB\perp AC\Rightarrow AE\perp AC;HF\perp AC\left(gt\right)\) => AE//HF
\(AC\perp AB\Rightarrow AF\perp AB;HE\perp AB\left(gt\right)\) => AF//HE
=> AEHF là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{BAC}=90^o\left(cmt\right)\)
=> AEHF là hình CN
b/
Xét tg vuông EHA và tg vuông ABC có
\(\widehat{EAH}=\widehat{ACB}\) (cùng phụ với \(\widehat{ABC}\) )
=> tg EHA đồng dạng với tg ABC
\(\Rightarrow\dfrac{AE}{AC}=\dfrac{HE}{AB}\)
Mà AEHF là hình CN (cmt) => HE=AF (cạnh đối HCN)
\(\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{AB}\Rightarrow AE.AB=AF.AC\left(dpcm\right)\)
c/
\(\widehat{BAC}=90^o\left(cmt\right)\)
d/
Xét tg vuông HFC có
\(HI=CI\left(gt\right)\Rightarrow FI=HI=CI=\dfrac{HC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> H; F; C cùng nằm trên đường tròn đường kính HC tâm I
=> đường tròn tâm I đường kính HC là đường tròn ngoại tiếp tg HFC
=> tg IHF cân tại I \(\Rightarrow\widehat{IFH}=\widehat{IHF}\)
Ta có
HF//AB (cùng vuông góc với AC) \(\Rightarrow\widehat{IHF}=\widehat{ABC}\) (góc đồng vị)
\(\Rightarrow\widehat{IFH}=\widehat{ABC}\) (1)
Xét tg vuông EAH và tg vuông HFE có
HE chung; AE=HF (cạnh đối hình CN) => tg EAH = tg HFE (Hai tg vuông có 2 cạnh góc vuông bàng nhau)
\(\Rightarrow\widehat{EAH}=\widehat{HFE}\)
Mà \(\widehat{EAH}=\widehat{ACB}\left(cmt\right)\)
\(\Rightarrow\widehat{HFE}=\widehat{ACB}\) (2)
Mà \(\widehat{ABC}+\widehat{ACB}=90^o\) (3)
Từ (1) (2) (3)
\(\Rightarrow\widehat{IFH}+\widehat{HFE}=\widehat{IFE}=\widehat{ABC}+\widehat{ACB}=90^o\)
=> EF là tiếp tuyến với (I)



d3//d2 \(\Rightarrow a=-1\)
d3 cắt d1 tại điểm có hoành độ bằng 1
\(\Rightarrow a+b=2\)
Ta có hệ
\(\left\{{}\begin{matrix}a=-1\\a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=3\end{matrix}\right.\)

B= \(\dfrac{2023}{2-x}\) biểu thức B xác định ⇔ \(2-x\) \(\ne\) 0; \(x\ne\) 2
Kết luận biểu thức B xác định khi và chỉ khi \(x\) ≠ 2

Do A cách trục tung một khoảng bằng 7 nên x = 7
Thay x = 7 vào y = 3x - 2, ta có:
y = 3.7 - 2 = 19
Vậy A(7; 19)
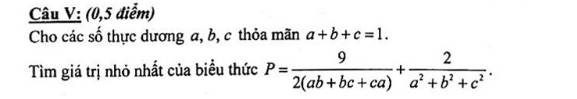 giúp e vs ạaa
giúp e vs ạaa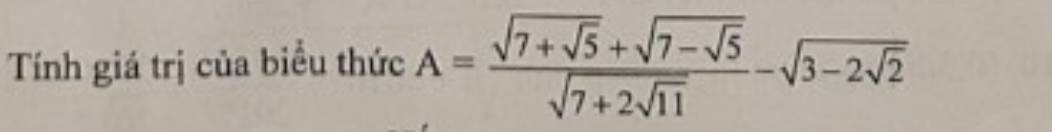
Lời giải:
HPT \(\Leftrightarrow \left\{\begin{matrix} 2(\sqrt{5}+2)x+2y=6-2\sqrt{5}\\ -x+2y=6-2\sqrt{5}\end{matrix}\right.\)
Lấy PT(1) trừ PT(2) theo vế:
$\Rightarrow 2(\sqrt{5}+2)x+x=(6-2\sqrt{5})-(6-2\sqrt{5})$
$\Leftrightarrow (2\sqrt{5}+5)x=0$
$\Leftrightarrow x=0$
$y=3-\sqrt{5}-(\sqrt{5}+2)x=3-\sqrt{5}-(\sqrt{5}+2).0=3-\sqrt{5}$