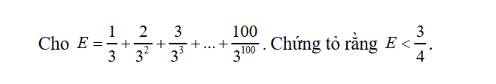
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Diện tích thửa ruộng là \(51\cdot30=1530\left(m^2\right)\)
b: Diện tích thửa ruộng sau khi tăng thêm là:
\(1530\left(1+10\%\right)=1683\left(m^2\right)\)
Chiều cao thửa ruộng là:
\(\dfrac{2\left(1683-1530\right)}{20}=15,3\left(m\right)\)
Tổng độ dài hai đáy là: \(1530\cdot2:15,3=200\left(m\right)\)

Số hoàn chỉnh là số có tổng các ước của nó(không kể chính nó) bằng chính nó
Vd: 6;28;...
Tổng các ước của 20 không kể 20 là:
1+2+4+5+10=22>20
=>20 ko là số hoàn chỉnh
Tổng các ước của 28 không kể 28 là:
1+2+4+7+14=28=28
=>28 là số hoàn chỉnh
Tổng các ước của 45 không kể 45 là:
1+3+5+9+15=33<45
=>45 không là số hoàn chỉnh
Tổng các ước của 128 không kể 128 là:
1+2+4+8+16+32+64=127<128
=>128 không là số hoàn chỉnh

\(\dfrac{\dfrac{5}{7}+\dfrac{5}{9}-\dfrac{5}{11}}{\dfrac{15}{7}+\dfrac{5}{9}-\dfrac{15}{11}}=\dfrac{\dfrac{495}{693}+\dfrac{385}{693}-\dfrac{315}{693}}{\dfrac{1485}{693}+\dfrac{385}{693}-\dfrac{945}{693}}\\ =\dfrac{\dfrac{565}{693}}{\dfrac{925}{693}}=\dfrac{565}{925}=\dfrac{113}{815}\)

a, \(S_{ABC}=\dfrac{1}{2}a.a=\dfrac{a^2}{2}\)
Theo Pytago tam giac ABC vuong tai B
\(AC=\sqrt{a^2+a^2}=\sqrt{2}a\Rightarrow AO=\dfrac{\sqrt{2}a}{2}\)
Theo Pytago tam giac SOA vuong tai O
\(SO=\sqrt{4a^2-\dfrac{2}{4}a^2}=\sqrt{\dfrac{14a^2}{4}}=\sqrt{\dfrac{7}{2}}a\)
\(V_{ABC}=\dfrac{1}{3}.\dfrac{a^2}{2}.\dfrac{\sqrt{7}}{\sqrt{2}}a=\dfrac{a^3\sqrt{7}}{6\sqrt{2}}\)
b, Ta co \(\dfrac{d\left(C;\left(SAB\right)\right)}{d\left(O;\left(SAB\right)\right)}=\dfrac{AC}{OA}=2\Rightarrow d\left(C;\left(SAB\right)\right)=2d\left(O;\left(SAB\right)\right)\)
Ke OH vuong AB, SO vuong AB, SO;OH chua (SOH)
=> AB vuong (SOH)
Ke OK vuong SH => OK la khoang cach
- bn tinh not nhe
c, ((SAB);(ABCD)) = ^SHO
- tinh dc phan b roi ap vao tam giac SHO la ra nhe

\(5^{16}:5^{14}+3^2+2000^0\)
\(=5^2+3^2+2000^0\)
\(=25+9+1\)
\(=35\)
\(3^{96}:3^{95}+2.2^3+1^{2024}\)
\(=3^1+2^4+1\)
\(=3+16+1\)
\(=20\)


Vì \(\widehat A\) và \(\widehat B\) bù nhau nên \(\widehat A+\widehat B=180^\circ\) (1)
Lại có: \(\widehat A-\widehat B=30^\circ\) (2)
Từ (1) và (2) \(\Rightarrow (\widehat A+\widehat B)+(\widehat A-\widehat B)=180^\circ+30^\circ\)
\(\Rightarrow2\widehat{A}=210^{\circ}\)
\(\Rightarrow\widehat{A}=\dfrac{210^{\circ}}{2}=105^{\circ}\)
Khi đó: \(105^{\circ}-\widehat{B}=30^{\circ}\Rightarrow\widehat{B}=105^{\circ}-30^{\circ}=75^{\circ}\)

Bài 1:
a; \(\dfrac{1}{n}\); \(\dfrac{1}{n+1}\) (n > 0; n \(\in\) Z)
\(\dfrac{1}{n}\) - \(\dfrac{1}{n+1}\) = \(\dfrac{n+1-1}{n.\left(n+1\right)}\) = \(\dfrac{1}{n\cdot\left(n+1\right)}\)
⇒ \(\dfrac{1}{n}\) - \(\dfrac{1}{n+1}\) = \(\dfrac{1}{n\left(n+1\right)}\) (đpcm)
Bài 1b
A = \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\) + \(\dfrac{1}{7.8}\) + \(\dfrac{1}{8.9}\)
A = \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) +\(\dfrac{1}{5}\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{8}\) + \(\dfrac{1}{8}\) - \(\dfrac{1}{9}\)
A = \(\dfrac{1}{2}\) - \(\dfrac{1}{9}\)
A = \(\dfrac{7}{18}\)


Ta có: \(E=\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\)
\(3E=1+\dfrac{2}{3}+\dfrac{3}{3^2}+...+\dfrac{100}{3^{99}}\)
\(3E-E=\left(1+\dfrac{2}{3}+\dfrac{3}{3^2}+..+\dfrac{100}{3^{99}}\right)-\left(\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\right)\)
\(2E=1+\dfrac{1}{3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\)
\(6E=3+1+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}-\dfrac{100}{3^{99}}\)
\(6E-2E=\left(3+1+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}-\dfrac{100}{3^{99}}\right)-\left(1+\dfrac{1}{3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\right)\)
\(4E=3-\dfrac{100}{3^{99}}-\dfrac{100}{3^{100}}\)
\(\Rightarrow E=\dfrac{3-\dfrac{100}{3^{99}}-\dfrac{100}{3^{100}}}{4}=\dfrac{3}{4}-\dfrac{\dfrac{100}{3^{99}}+\dfrac{100}{3^{100}}}{4}< \dfrac{3}{4}\) (đpcm)