Gọi chiều dài màn hình là `x` (cm) 

ĐK: `x>0` 

Đổi: 17inch ≃ 43,18 (cm) 

Chiều cao màn hình là: `5/8x(cm)` 

Áp dụng định lý Pythagore ta có: 

\(x^2+\left(\dfrac{5}{8}x\right)^2=43,18^2\\ < =>x^2+\dfrac{25}{64}x^2=1864,5124\\ < =>\dfrac{79}{64}x^2=1864,5124\\ < =>x^2\approx1510,4\\ < =>x\approx38,9\left(cm\right)\left(x>0\right)\)

=> Chiều cao của màn hình là: `5/8*38,9≃24,3(cm)` 

Vậy: 

Gọi x (cm) là chiều rộng màn hình (x > 0)

Chiều dài màn hình là:

  Đổi 17 inch ≈ 43,2 cm

  Theo đề bài, ta có phương trình:

⇒ x ≈ 22,9 (cm)

Vậy chiều rộng màn hình là 22,9 cm, chiều dài màn hình là 22,9.1,6 ≈ 36,6 cm

a.

\(\left\{{}\begin{matrix}S=x_1+x_2=7\\P=x_1x_2=10\end{matrix}\right.\)

Theo định lý Viet đảo, \(x_1;x_2\) là nghiệm:

\(x^2-7x+10=0\)

Trình bày tương tự câu a ta có:

b.

\(x^2-2x-35=0\)

c.

\(x^2+13x+36=0\)

Giá sau khi giảm so với giá bìa:

1 - 40% = 60%

Giá bìa quyển sách là:

69600 : 60% = 116000 (đồng)

`2/5 + 3/4 :x= -1/2 `

`=> 3/4 :x = -1/2 - 2/5`

`=> 3/4 : x = -9/10`

`=> x = 3/4 : (-9/10)`

`=> x = 3/4 . (-10/9) `

`=> x = -5/6`

Vậy `x = -5/6`

------------------

`5/7 - 2/3 x = 4/5`

`=> 2/3 x = 5/7 - 4/5`

`=> 2/3 x = -3/35`

`=> x = -3/35 : 2/3`

`=> x = -3/35 . 3/2`

`=> x = -9/70`

Vậy `x = -9/70`

------------------

`1/2 x + 3/5 x = -2/3`

`=> (1/2 + 3/5) x = -2/3`

`=> 11/10 x = -2/3`

`=> x = -2/3 : 11/10`

`=> x = -2/3 . 10/11`

`=> x = -20/33`

Vậy ` x = -20/33`

------------------

`4/7 x - x = -9/14`

`=> (4/7 - 1) x = -9/14`

`=> -3/7 x = -9/14`

`=> 3/7 x = 9/14`

`=> x = 9/14 : 3/7`

`=> x = 9/14 . 7/3`

`=> x = 3/2`

Vậy `x = 3/2`

\(-x^3+3x-7+2m=0\)

\(\Leftrightarrow x^3-3x+7=2m\)

Xét hàm: \(f\left(x\right)=x^3-3x+7\)

\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)

Bảng biến thiên:

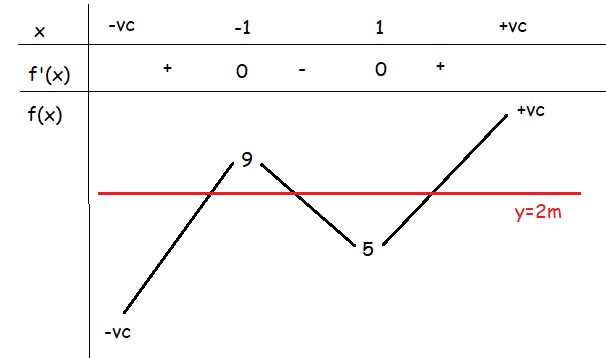
Từ BBT ta thấy pt có 3 nghiệm pb hay \(y=2m\) cắt \(y=f\left(x\right)\) tại 3 điểm pb

\(\Leftrightarrow5< 2m< 9\Rightarrow\dfrac{5}{2}< m< \dfrac{9}{2}\)

\(\left(2x-\dfrac{1}{3}\right)^2=-\dfrac{8}{15}\times\dfrac{15}{27}:\left(2x-\dfrac{1}{3}\right)\)

\(\left(2x-\dfrac{1}{3}\right)^2\times\left(2x-\dfrac{1}{3}\right)=-\dfrac{8}{27}\)

\(\left(2x-\dfrac{1}{3}\right)^3=\left(-\dfrac{2}{3}\right)^3\)

\(2x-\dfrac{1}{3}=-\dfrac{2}{3}\)

\(2x=\dfrac{1}{3}-\dfrac{2}{3}\)

\(2x=-\dfrac{1}{3}\)

\(x=-\dfrac{1}{6}\)

Áp dụng t/c dãy tỉ số bằng nhau: \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\)

Từ \(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\Rightarrow\dfrac{\left(a+b\right)^3}{\left(c+d\right)^3}=\dfrac{a^3}{c^3}=\dfrac{b^3}{d^3}=\dfrac{a^3+b^3}{c^3+d^3}\)

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)

Ta có: \(VT=\dfrac{a^3+b^3}{c^3+d^3}=\dfrac{bk^3+b^3}{dk^3+d^3}=\dfrac{b.\left(k+1\right)^3}{d.\left(k+1\right)^3}=\dfrac{b}{d}\)

\(VP=\dfrac{\left(a+b\right)^3}{\left(c+d\right)^3}=\dfrac{\left(bk+b\right)^3}{\left(dk+d\right)^3}=\dfrac{b.\left(k+1\right)^3}{d.\left(k+1\right)^3}=\dfrac{b}{d}\)

Vậy \(VT=VP\left(đpcm\right)\)

____________

VT = vế trái

VP = vế phải

\(#NqHahh\)

`(1/3)^(2x - 1) = 3^5`

`=> (3^(-1))^(2x - 1) = 3^5`

`=> 3^(-1.(2x-1)) =  3^5`

`=> 3^(1-2x) = 3^5`

`=> 1 - 2x = 5`

`=> 2x = 1 - 5`

`=> 2x = -4`

`=> x = -2`

Vậy `x = -2`

Gọi số tự nhiên bé hơn là `x `

Điều kiện: `x ∈ N`

=> Số tự nhiên lớn hơn là: `x + 1`

Do hiệu các bình phương của bằng `39`

`=> (x+1)^2 - x^2 = 39`

`=> x^2 + 2x + 1 - x^2 = 39`

`=> 2x = 38`

`=> x = 38 : 2`

`=> x = 19`

Vậy số tự nhiên bé hơn là `19`, số tự nhiên lớn hơn là `19+ 1 = 20`