2\(\sqrt{3}\) - \(\sqrt{4+x^2}\) = 0    vì 4 + \(x^2\) ≥ 0 ∀ \(x\) vậy \(\sqrt{4+x^2}\) có nghĩa với ∀\(x\)

2\(\sqrt{3}\) - \(\sqrt{4+x^2}\) = 0

          \(\sqrt{4+x^2}\)  = 2\(\sqrt{3}\)

           4 + \(x^2\)   = 12

                \(x^2\)      = 12 - 4

                \(x^2\)      = 8

               \(\left[{}\begin{matrix}x=-\sqrt{8}\\x=\sqrt{8}\end{matrix}\right.\)

               \(\left[{}\begin{matrix}x=-2\sqrt{2}\\x=2\sqrt{2}\end{matrix}\right.\)

                \(\left[{}\begin{matrix}x=-2\sqrt{2}\\x=2\sqrt{2}\end{matrix}\right.\)

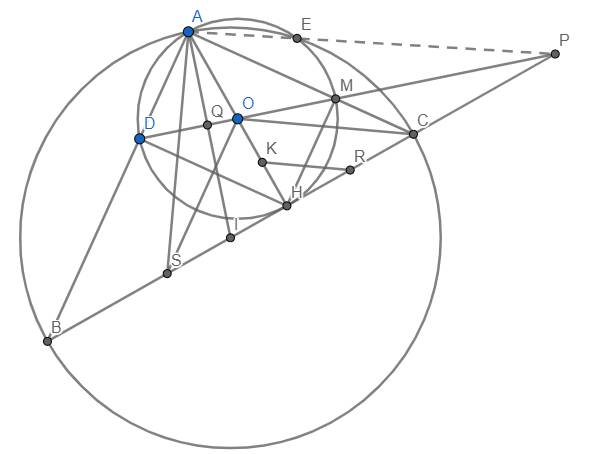
a) Chứng minh tam giác ABH vuông tại H và \(DH\perp AB\) rồi dùng hệ thức lượng \(\Rightarrow AD.AB=AH^2\). Tương tự, ta có \(AM.AC=AH^2\). Do đó \(AD.AB=AM.AC\) và theo bổ đề quen thuộc thì tứ giác BCMD nội tiếp. (đpcm)

b) Gọi Q là giao điểm của DM và AI. Khi đó tam giác ABC vuông tại A có trung tuyến AI nên \(IA=IB=IC=\dfrac{BC}{2}\) hay tam giác IBA cân tại I, suy ra \(\widehat{B}=\widehat{DAQ}\).

 Lại có \(\widehat{B}+\widehat{ACB}=90^o\) suy ra \(\widehat{DAQ}+\widehat{ADQ}=90^o\) (do \(\widehat{ADQ}=\widehat{ACB}\) (cmt)). Do đó \(PQ\perp AI\) tại Q. Từ đó dễ dàng chứng minh O là trực tâm tam giác AIP.

 c) Do tứ giác BCMD nội tiếp nên \(PM.PD=PC.PB\) \(\Rightarrow P_{P/\left(O\right)}=P_{P/\left(I\right)}\) \(\Rightarrow\) P nằm trên trục đẳng phương của (O) và (I). Lại có AE chính là trục đẳng phương của (O) và (I) nên A, E, P thẳng hàng. (đpcm)

 d) Ta thấy SO//AB \(\perp AC\) và \(AH\perp BC\) nên O là trực tâm tam giác ASC \(\Rightarrow OC\perp AS\)

 Lại có OC//KR nên \(RK\perp SA\) (đpcm)

 Ở bài này chứng minh được \(A\in\left(I\right)\) vì BC là đường kính của (I) và \(\widehat{BAC}=90^o\)

Gọi x (đồng) là giá niêm yết của tivi (x > 0)

⇒ 24000000 - x (đồng) là giá niêm yết của máy lạnh

Giá tivi sau khi giảm:

x - 0,1x = 0,9x (đồng)

Giá máy lạnh sau khi giảm:

24000000 - x - (24000000 - x).0,25 = 24000000 - x - 6000000 + 0,25x = 18000000 - 0,75x (đồng)

Theo đề bài ta có phương trình:

0,9x + 18000000 - 0,75x = 20250000

⇔ 0,15x = 20250000 - 18000000

⇔ 0,15x = 2250000 (đồng)

⇔ x = 2250000 : 0,15

⇔ x = 15000000 (nhận)

Vậy giá niêm yết của tivi là 15000000

Giá niêm yết của máy lạnh là 24000000 - 15000000 = 9000000 (đồng)

Gọi x (đồng) là giá niêm yết của tivi (x > 0)

⇒ 24000000 - x (đồng) là giá niêm yết của máy lạnh

Giá tivi sau khi giảm:

x - 0,1x = 0,9x (đồng)

Giá máy lạnh sau khi giảm:

24000000 - x - (24000000 - x).0,25 = 24000000 - x - 6000000 + 0,25x = 18000000 - 0,75x (đồng)

Theo đề bài ta có phương trình:

0,9x + 18000000 - 0,75x = 20250000

⇔ 0,15x = 20250000 - 18000000

⇔ 0,15x = 2250000 (đồng)

⇔ x = 2250000 : 0,15

⇔ x = 15000000 (nhận)

Vậy giá niêm yết của tivi là 15000000

Giá niêm yết của máy lạnh là 24000000 - 15000000 = 9000000 (đồng)

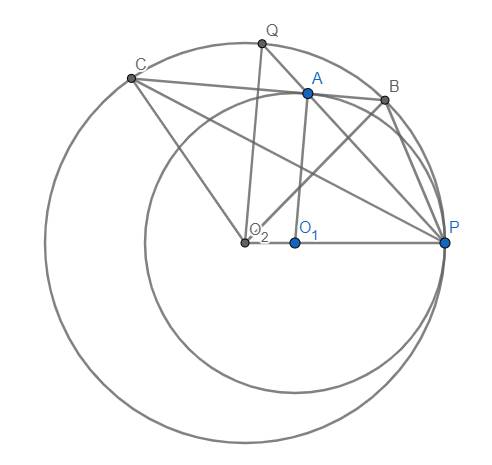
 Gọi Q là giao điểm của PA và (O₂). Do \(\widehat{O_1AP}=\widehat{O_1PA}=\widehat{O_2PQ}=\widehat{O_2QP}\) nên O₁A//O₂Q

 Mặt khác, \(BC\perp O_1A\) (vì BC là tiếp tuyến tại A của (O₁) nên \(BC\perp O_2Q\)

 \(\Rightarrow\) Q là điểm chính giữa của cung nhỏ BC 

 \(\Rightarrow\) PQ là tia phân giác \(\widehat{BPC}\) \(\Rightarrow\) đpcm

 Nếu như theo kiến thức lớp 9 chưa học về đồ thị nào khác ngoài đồ thị bậc nhất (là 1 đường thẳng) thì 2 dạng bài này gần như tương đương nhau. Nhưng khi bạn lên cấp III và học những loại đồ thị đường cong bậc hai (ellipse, parabol, hyperbol, đường tròn,...) thì 2 dạng bài này rõ ràng khác xa nhau nhé. (Vì xác định hàm số thì đó có thể là hàm số kiểu gì cũng được, nhưng viết ptđt thì chỉ có liên quan đến đường thẳng thôi.)

Lời giải:
a. 

\(M=\frac{x}{\sqrt{x}(\sqrt{x}-1)}-\frac{2\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-1)}=\frac{x-(2\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-1)}\\ =\frac{x-2\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-1)}=\frac{(\sqrt{x}-1)^2}{\sqrt{x}(\sqrt{x}-1)}\\ =\frac{\sqrt{x}-1}{\sqrt{x}}\)

b.

$M=-2\Leftrightarrow \frac{\sqrt{x}-1}{\sqrt{x}}=-2$

$\Leftrightarrow \sqrt{x}-1=-2\sqrt{x}$

$\Leftrightarrow 3\sqrt{x}=1\Leftrightarrow x=\frac{1}{9}$ (tm)