Cho đường tròn (O) và điểm M nằm ngoài đường tròn (O). Vẽ các tiếp tuyến MA, MB và cát tuyết MCD. a/ Chứng minh : Tứ giác MAOB nội tiếp đường tròn và chỉ ra tâm của đường tròn đó . b/ Biết góc AOB=120, tam giác MAB là tam giác gì . c/ chứng minh MC.MD=MA^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(sđ\stackrel\frown{BC}=\widehat{BOC}=2\cdot\widehat{BAC}=120^0\)
b: M là điểm chính giữa của cung BC
=>\(sđ\stackrel\frown{MB}=sđ\stackrel\frown{MC}=\dfrac{sđ\stackrel\frown{BC}}{2}=60^0\)
Xét (O) có \(\widehat{AIB}\) là góc có đỉnh ở bên trong đường tròn chắn hai cung AB và MC
nên \(\widehat{AIB}=\dfrac{1}{2}\cdot\left(sđ\stackrel\frown{AB}+sđ\stackrel\frown{MC}\right)\)
=>\(\widehat{AIB}=\dfrac{1}{2}\left(sđ\stackrel\frown{AB}+sđ\stackrel\frown{MB}\right)=\dfrac{1}{2}\left(100^0+60^0\right)=80^0\)
Xét (O) có
\(\widehat{AMC}\) là góc nội tiếp chắn cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{AMC}=\widehat{ABC}=70^0\)
=>\(\widehat{AIB}>\widehat{AMC}\)

a) \(P=\dfrac{x}{\left(\sqrt{x}+\sqrt{y}\right)\left(1-\sqrt{y}\right)}-\dfrac{y}{\left(\sqrt{x}+\sqrt{y}\right)\left(1+\sqrt{x}\right)}-\dfrac{xy}{\left(\sqrt{x}+1\right)\left(1-\sqrt{y}\right)}\)
ĐK: \(\left\{{}\begin{matrix}x\ge0;y\ge0\\\sqrt{x}+\sqrt{y}\ne0\\\sqrt{x}+1\ne0\\1-\sqrt{y}\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0;y\ge0\\x^2+y^2>0\\y\ne1\end{matrix}\right.\)
\(P=\dfrac{x\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}-\dfrac{y\left(1-\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}-\dfrac{xy\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{x\sqrt{x}+x-y+y\sqrt{y}-xy\sqrt{x}-xy\sqrt{y}}{\left(\sqrt{x}+\sqrt{y}\right)\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{\left(x\sqrt{x}+y\sqrt{y}\right)+\left(x-y\right)-\left(xy\sqrt{x}+xy\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)+\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)-xy\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y+\sqrt{x}-\sqrt{y}-xy\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{\left(x-xy\right)+\left(-\sqrt{y}+y\right)+\left(\sqrt{x}-\sqrt{xy}\right)}{\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{x\left(1-y\right)-\sqrt{y}\left(1-\sqrt{y}\right)+\sqrt{x}\left(1-\sqrt{y}\right)}{\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{x\left(1-\sqrt{y}\right)\left(1+\sqrt{y}\right)-\sqrt{y}\left(1-\sqrt{y}\right)+\sqrt{x}\left(1-\sqrt{y}\right)}{\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{\left(1-\sqrt{y}\right)\left(x+x\sqrt{y}-\sqrt{y}+\sqrt{x}\right)}{\left(1-\sqrt{y}\right)\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{x+x\sqrt{y}-\sqrt{y}+\sqrt{x}}{\sqrt{x}+1}\)
\(P=\dfrac{\left(x+\sqrt{x}\right)+\left(x\sqrt{y}-\sqrt{y}\right)}{\sqrt{x}+1}\)
\(P=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+\sqrt{y}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+1}\)
\(P=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+\sqrt{xy}-\sqrt{y}\right)}{\sqrt{x}+1}\)
\(P=\sqrt{x}+\sqrt{xy}-\sqrt{y}\)
b) \(P=2\) khi:
\(\sqrt{x}+\sqrt{xy}-\sqrt{y}=2\)
\(\Leftrightarrow\sqrt{x}\left(\sqrt{y}+1\right)-\sqrt{y}-1=2-1\)
\(\Leftrightarrow\sqrt{x}\left(\sqrt{y}+1\right)-\left(\sqrt{y}+1\right)=1\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(\sqrt{y}+1\right)=1\)
Mà: x,y là nguyên \(\Rightarrow\sqrt{x}-1,\sqrt{y}+1\inƯ\left(1\right)=\left\{1;-1\right\}\)
Mặt khác: \(\sqrt{y}+1\ge1\) nên ta có:
\(\sqrt{y}+1=1\Leftrightarrow y=0\) (tm)
\(\Rightarrow\sqrt{x}-1=1\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\) (tm)
Vậy: \(\left(x;y\right)=\left(4;0\right)\)

\(P=\left(a^2+\dfrac{1}{16}+\dfrac{1}{16}+\dfrac{1}{16}\right)+\left(b^2+\dfrac{1}{16}+\dfrac{1}{16}+\dfrac{1}{16}\right)-\dfrac{3}{8}\)
\(P\ge4\sqrt[4]{\dfrac{a^2}{16^3}}+4\sqrt[4]{\dfrac{b^2}{16^3}}-\dfrac{3}{8}=\dfrac{1}{2}\left(\sqrt{a}+\sqrt{b}\right)-\dfrac{3}{8}=\dfrac{1}{8}\)
\(P_{min}=\dfrac{1}{8}\) khi \(a=b=\dfrac{1}{4}\)
Do \(\left\{{}\begin{matrix}a;b\ge0\\\sqrt{a}+\sqrt{b}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}0\le a\le1\\0\le b\le1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{a}\ge a^2\\\sqrt{b}\ge b^2\end{matrix}\right.\)
\(\Rightarrow a^2+b^2\le\sqrt{a}+\sqrt{b}=1\)
\(P_{max}=1\) khi \(\left(a;b\right)=\left(1;0\right);\left(0;1\right)\)

Do (d) đi qua A nên:
\(0.m+n=-1\Rightarrow n=-1\)
\(\Rightarrow y=mx-1\)
Pt hoành độ giao điểm (P) và (d):
\(\dfrac{1}{2}x^2=mx-1\Leftrightarrow x^2-2mx+2=0\) (1)
(d) tiếp xúc (P) khi và chỉ khi (1) có nghiệm kép
\(\Rightarrow\Delta'=m^2-2=0\Rightarrow m=\pm\sqrt{2}\)
- Với \(m=\sqrt{2}\Rightarrow x=-\dfrac{b}{2a}=\sqrt{2}\Rightarrow y=\dfrac{1}{2}x^2=1\)
Tọa độ tiếp điểm là \(\left(\sqrt{2};1\right)\)
- Với \(m=-\sqrt{2}\Rightarrow x=-\dfrac{b}{2a}=-\sqrt{2}\Rightarrow y=1\)
Tọa độ tiếp điểm là \(\left(-\sqrt{2};1\right)\)

Ta có pt: \(x^2-2mx+m^2=0\)
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot m^2=0\)
Khi phương trình luôn có nghiệm kép với mọi m \(\Rightarrow x_1< x_2\) vô lý
Chỉ có thể tìm được m nếu \(2000< x_1=x_2< 2007\)
Khi đó: \(x_1=x_2=\dfrac{-\left(-2m\right)}{2}=m\)
\(\Rightarrow2000< m< 2007\)
Các số nguyên m thỏa mãn là:
\(m\in\left\{2001;2002;2003;2004;2005;2006\right\}\)

ĐKXĐ: \(x\ge-\dfrac{1}{2};x\ne0\)
\(\dfrac{1}{x^2}-\dfrac{1}{x}=\sqrt{2x+1}-\sqrt{x+2}\)
\(\Leftrightarrow-\dfrac{x-1}{x^2}=\dfrac{x-1}{\sqrt{2x+1}+\sqrt{x+2}}\)
\(\Leftrightarrow\left(x-1\right)\left(\dfrac{1}{\sqrt{2x+1}+\sqrt{x+2}}+\dfrac{1}{x^2}\right)=0\)
\(\Leftrightarrow x-1=0\) (do \(\dfrac{1}{\sqrt{2x+1}+\sqrt{x+2}}+\dfrac{1}{x^2}\) luôn dương)
\(\Leftrightarrow x=1\)
Đk: \(x\ge-\dfrac{1}{2},x\ne0\)
pt \(\Leftrightarrow\dfrac{1}{x^2}-\dfrac{1}{x}=\sqrt{2x+1}-\sqrt{x+2}\)
\(\Leftrightarrow\dfrac{1-x}{x^2}=\dfrac{2x+1-\left(x+2\right)}{\sqrt{2x+1}+\sqrt{x+2}}\)
\(\Leftrightarrow\dfrac{1-x}{x^2}=\dfrac{x-1}{\sqrt{2x+1}+\sqrt{x+2}}\)
\(\Leftrightarrow\left(x-1\right)\left(\dfrac{1}{\sqrt{2x+1}+\sqrt{x+2}}+\dfrac{1}{x^2}\right)=0\)
\(\Leftrightarrow x=1\) (vì \(\dfrac{1}{\sqrt{2x+1}+\sqrt{x+2}}+\dfrac{1}{x^2}>0\))
Vậy \(S=\left\{1\right\}\)

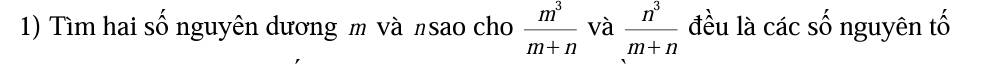
a.
Do MA là tiếp tuyến \(\Rightarrow MA\perp OA\)
\(\Rightarrow M,A,O\) cùng thuộc đường tròn đường kính OM
Do MB là tiếp tuyến \(\Rightarrow MB\perp OB\)
\(\Rightarrow M,B,O\) cùng thuộc đường tròn đường kính OM
\(\Rightarrow\) Tứ giác MAOB nội tiếp đường tròn đường kính OM
Do OM là đường kính nên tâm đường tròn là trung điểm OM.
b.
Do MAOB nội tiếp \(\Rightarrow\widehat{AOB}+\widehat{AMB}=180^0\)
\(\Rightarrow\widehat{AMB}=180^0-120^0=60^0\) (1)
Lại có M là giao điểm 2 tiếp tuyến tại A và B
\(\Rightarrow MA=MB\)
\(\Rightarrow\Delta AMB\) cân tại M (2)
(1);(2) \(\Rightarrow\Delta AMB\) đều (tam giác cân có 1 góc bằng 60 độ)
c.
Xét hai tam giác MAC và MDA có:
\(\left\{{}\begin{matrix}\widehat{AMC}\text{ chung}\\\widehat{MAC}=\widehat{MDA}\left(\text{cùng chắn AC}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MAC\sim\Delta MDA\left(g.g\right)\)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{MC}{MA}\Rightarrow MC.MD=MA^2\)