⇒ Đáp án đúng là: d 9

Chọn B. 1320

a: Đặt a/b=c/d=k

=>\(a=bk;c=dk\)

\(\left(\dfrac{a-b}{c-d}\right)^2=\left(\dfrac{bk-b}{dk-d}\right)^2=\left(\dfrac{b\left(k-1\right)}{d\left(k-1\right)}\right)^2=\left(\dfrac{b}{d}\right)^2\)

\(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot k}=\dfrac{b^2\cdot k}{d^2\cdot k}=\dfrac{b^2}{d^2}\)

Do đó: \(\left(\dfrac{a-b}{c-d}\right)^2=\dfrac{ab}{cd}\)

b: \(\left(\dfrac{a+b}{c+d}\right)^3=\left(\dfrac{bk+b}{dk+d}\right)^3=\left(\dfrac{b\left(k+1\right)}{d\left(k+1\right)}\right)^3=\left(\dfrac{b}{d}\right)^3\)

\(\dfrac{a^3-b^3}{c^3-d^3}=\dfrac{b^3k^3-b^3}{d^3k^3-d^3}=\dfrac{b^3\left(k^3-1\right)}{d^3\left(k^3-1\right)}=\dfrac{b^3}{d^3}\)

Do đó: \(\left(\dfrac{a+b}{c+d}\right)^3=\dfrac{a^3-b^3}{c^3-d^3}\)

Trên tia ssoois của MA lấy D sao cho DM=AM

Mà BM=CM (gt)

=> ABCD là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

Ta có \(\widehat{A}=90^o\)

=> ABCD là hình chữ nhật => AD=BC (trong HCN hai đường chéo bằng nhau)

Ta có

\(AM=\dfrac{AD}{2}\) mà \(AD=BC\left(cmt\right)\Rightarrow AM=\dfrac{BC}{2}\) 

Gọi tam giác vuông đề bài cho là ΔABC vuông tại A, đường trung tuyến AM

Trên tia đối của tia MA, lấy D sao cho MA=MD

Xét ΔMAB và ΔMDC có

MA=MD

\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)

MB=MC

Do đó: ΔMAB=ΔMDC

=>\(\widehat{MAB}=\widehat{MDC}\)

=>AB//DC

Ta có: AB//DC

AB\(\perp\)AC

Do đó: CD\(\perp\)CA

Xét ΔBAC vuông tại A và ΔDCA vuông tại C có

BA=DC

AC chung

Do đó: ΔBAC=ΔDCA

=>BC=DA

mà DA=2AM

nên BC=2AM

=>\(AM=\dfrac{1}{2}BC\)(ĐPCM)

      Giải:

Vì DE // BC  

   \(\dfrac{AD}{AB}\) = \(\dfrac{AE}{AC}\)  (hệ quả Thalet)

⇒ \(\dfrac{2}{AB}\) = \(\dfrac{4}{10}\)

    AB = 2 : \(\dfrac{4}{10}\) 

   AB = 5 

Vậy AB =  5 cm

AB = AD + BD 

BD = AB - AD 

BD = 5 -  2 = 3

Vậy BD = 3cm

Kết luận: BD =  3cm

Ta có:

EC = AC - AE = 10 - 4 = 6

∆ABC có:

DE // BC (gt)

⇒ AD/BD = AE/EC (định lý Thales)

⇒ 2/BD = 4/6

⇒ BD = 2 . 6 : 4 = 3

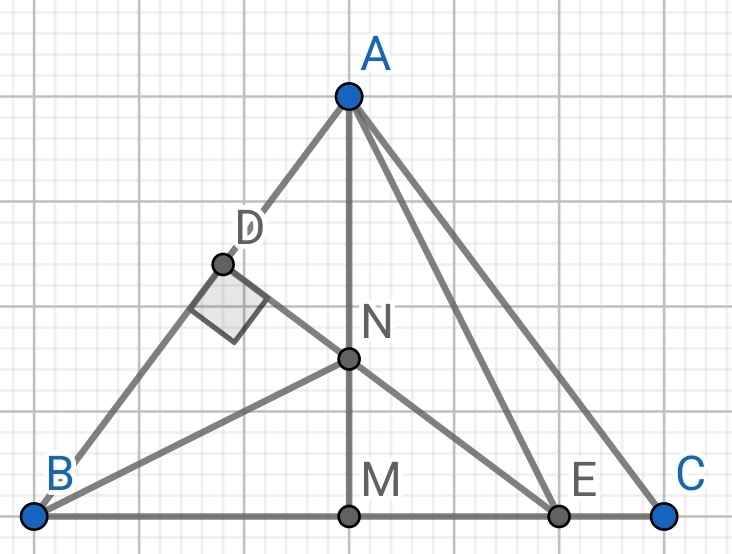
a) ∆ABC cân tại A (gt)

M là trung điểm của BC (gt)

⇒ AM là đường trung tuyến của ∆ABC

⇒ AM cũng là đường cao của ∆ABC

⇒ AM ⊥ BC tại M

Do M là trung điểm của BC (gt)

⇒ MB = MC

Xét hai tam giác vuông: ∆ABM và ∆ACM có:

AM là cạnh chung

MB = MC (cmt)

⇒ ∆ABM = ∆ACM (hai cạnh góc vuông)

b) Ta có:

AM ⊥ BC (cmt)

⇒ AM ⊥ BE

⇒ AM là đường cao của ∆ABE

Lại có:

ND ⊥ AB (gt)

⇒ ED ⊥ AB

⇒ ED là đường cao thứ hai của ∆ABE

Mà ED cắt AM tại N

⇒ BN là đường cao thứ ba của ∆ABE

⇒ BN ⊥ AE

c) Do BN là tia phân giác của ∠ABC (gt)

⇒ ∠ABN = ∠CBN

⇒ ∠DBN = ∠MBN

Xét hai tam giác vuông: ∆BND và ∆BNM có:

BN là cạnh chung

∠DBN = ∠MBN (cmt)

⇒ ∆BND = ∆BNM (cạnh huyền - góc nhọn)

⇒ ND = NM (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆ADN và ∆EMN có:

ND = NM (cmt)

∠AND = ∠ENM (đối đỉnh)

⇒ ∆ADN = ∆EMN (cạnh góc vuông - góc nhọn kề)

⇒ AN = EN (hai cạnh tương ứng)

⇒ ∆ANE cân tại N

a: Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

Do đó: ΔABM=ΔACM

b: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM\(\perp\)BC tại M

Xét ΔEAB có

ED,AM là các đường cao

ED cắt AM tại N

Do đó: N là trực tâm của ΔEAB

=>BN\(\perp\)AE

c: Xét ΔBAE có

BN là đường cao

BN là đường phân giác

Do đó: ΔBAE cân tại B

=>BA=BE

Xét ΔBNE và ΔBNA có

BN chung

\(\widehat{NBE}=\widehat{NBA}\)

BE=BA

Do đó: ΔBNE=ΔBNA

=>NE=NA

=>ΔNEA cân tại N

a: Xét ΔKNP vuông tại K và ΔHPN vuông tại H có

NP chung

\(\widehat{KNP}=\widehat{HPN}\)

Do đó: ΔKNP=ΔHPN

b: ΔKNP=ΔHPN

=>\(\widehat{KPN}=\widehat{HNP}\)

=>\(\widehat{ENP}=\widehat{EPN}\)

=>EN=EP

Xét ΔMEN và ΔMEP có

ME chung

EN=EP

MN=MP

Do đó: ΔMEN=ΔMEP

=>\(\widehat{NME}=\widehat{PME}\)

=>ME là phân giác của góc NMP

                Giải

Diện tích xung quanh của bể hình lăng trụ là:

        2,6 x 4 x 1,2  = 12,48 (m²)

Diện tích đáy bể là: 

       2,6 x 2,6 = 6,76 (m²)

Diện tích bể cần lát gạch là:

    12,48 + 6,76 = 19,24 (m²)

Diện tích một viên gạch là:

     40 x 30 = 1200 (cm²)

   1200cm² = 0,12m²

Vì 19,24 : 0,12 = 160,3

Vậy cần ít nhất số viên gạch để lát bể là:

    160 + 1  = 161 (viên)

Đáp số: ....

              Giải:

Ta có:    Xét tam giác vuông ABC vuông tại B nên cạnh AC là cạnh huyền, ta có: 

                 AC > AB ⁽¹⁾ (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)

            \(\widehat{ADB}\)  < 90⁰ (vì tam giác ADB vuông tại B)

           \(\widehat{ACD}\) = \(\widehat{ABC}\) + \(\widehat{BAC}\) (Góc ngoài tam giác bằng tổng hai góc trong không kề với nó)

        ⇒  \(\widehat{ACD}\)  = 90⁰ + \(\widehat{BAC}\) > \(\widehat{ADB}\)  = \(\widehat{ADC}\)

Xét tam giác ADC  có: 

            \(\widehat{ACD}\) > \(\widehat{ADC}\) (cmt)

            AD > AC ⁽²⁾(Trong tam giác góc đối diện với cạnh lớn hơn thì lớn hơn và ngược lại)

Chứng minh tương tự ta có:

         AE > AD ⁽³⁾

Từ (1) và (2) và (3) ta có:

       AE > AD > AC > AB 

Kết luận: AE > AD > AC > AB 

Câu 5:

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔBAD=ΔBED

b: ΔBAD=ΔBED

=>DA=DE

mà DE<DC(ΔDEC vuông tại E)

nên DA<DC
ΔBAD=ΔBED

=>\(\widehat{BDA}=\widehat{BDE}\)

mà \(\widehat{BDA}=\widehat{DBK}\)(BK//AC)

nên \(\widehat{KBD}=\widehat{KDB}\)

=>ΔKBD cân tại K