Ông Việt bị bệnh cao huyết áp nên mỗi buổi sáng phải uống 1 viên thuốc hàm lượng 200mg. Sau mỗi ngày thuốc trong người ông còn lại 10%. Ước tính lượng thuốc trong người ông trong khoảng thời gian dài
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

\(y=\dfrac{x^2-\left(x^2+4mx+1\right)}{x+\sqrt{x^2+4mx+1}}=\dfrac{-4mx-1}{x+\sqrt{x^2+4mx+1}}\)
\(=\dfrac{-4mx-1}{x+\left|x\right|\sqrt{1+\dfrac{4m}{x}+\dfrac{1}{x^2}}}\)
\(\lim\limits_{x\rightarrow\pm\infty}y\dfrac{-4m-\dfrac{1}{x}}{1\pm\sqrt{1+\dfrac{4m}{x}+\dfrac{1}{x^2}}}=-4m\)
Để y = 1 là TCN => -4m = 1 => m = -1/4

a, Ta có (AC;AB) = ^BAC
tan^BAC = BC/AB = 1 => ^BAC = 450
b, Ta có BD // B'D'
=> (AD';BD) = (AD';B'D') = ^AD'B'
Xét tam giác AD'B' ta có AB' = B'D' = AD'
=> tam giác AD'B' đều => ^AD'B' = 600
c, Ta có BD vuông AC ; BD vuông CC'
=> BD vuông (ACC')
Mà AC' thuộc (ACC') => AC' vuông BD


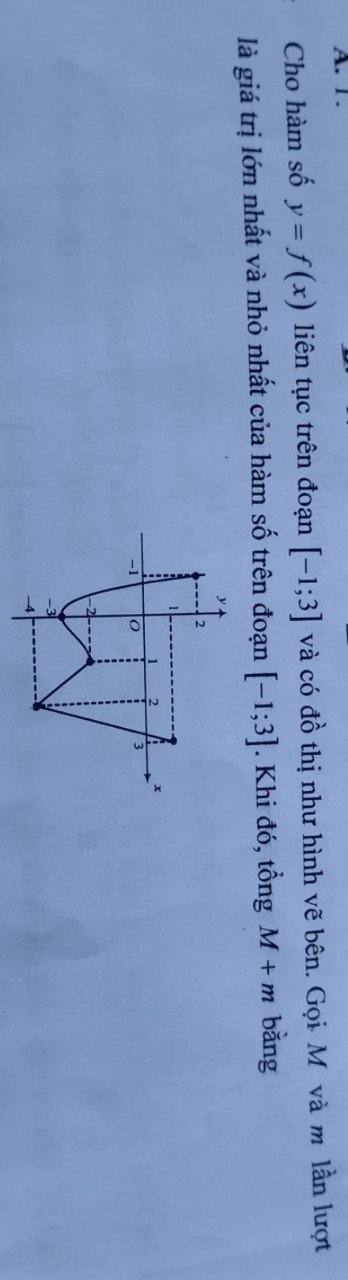
Dựa vào đồ thị, ta thấy \(m=\min\limits_{\left[-1;3\right]}f\left(x\right)=f\left(2\right)=-4\)
và \(M=\max\limits_{\left[-1;3\right]}f\left(x\right)=f\left(-1\right)=2\)
Khi đó \(M+m=2-4=-2\)

Có \(y'=x^2-2mx-1\)
Xét pt \(y'=x^2-2mx-1=0\)(*), có \(\Delta'=m^2+1>0\) nên (*) luôn có 2 nghiệm phân biệt \(x_1,x_2\)
Theo định lý Viète, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-1\end{matrix}\right.\)
Để \(x_1^2+x_2^2=2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=2\)
\(\Leftrightarrow\left(2m\right)^2+2=2\)
\(\Leftrightarrow4m^2=0\)
\(\Leftrightarrow m=0\)
Vậy \(m=0\) thỏa mãn ycbt.

a, A''Có đúng 2 nữ''
\(C^2_3.C_{56}^2\)
\(P\left(A\right)=\dfrac{C_3^2.C_{56}^2}{C_{59}^4}\)
b, B''Có ít nhất 2 nam''
TH1 : Có 2 nam \(C_{56}^2.C_3^2\)
TH2 : Có 3 nam \(C_{56}^3.C_3^1\)
TH3 : Có 4 nam \(C^4_{56}\)
\(\Rightarrow C_{56}^2.C_3^2+C_{56}^3.C_3^1+C_{56}^4\)
\(P\left(B\right)=\dfrac{C_{56}^2.C_3^2+C_{56}^3.C_3^1+C_{56}^4}{C_{59}^4}\)
c, C''Có nhiều nhất 2 nam''
TH1 : Có 1 nam \(C_{56}^1.C_3^3\)
TH2 : Có 2 nam \(C_{56}^2.C_3^2\)
\(\Rightarrow C_{56}^2.C_3^3+C_{56}^2.C_3^2\)
\(P\left(C\right)=\dfrac{C_{56}^2.C_3^3+C^2_{56}.C_3^2}{C_{59}^4}\)