Một hộp có 30 thẻ cùng loại, mỗi thẻ được ghi một trong các số 1,2,3,...,30. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố số xuất hiện trên thẻ là số khi chia cho 6 dư 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1; (\(\dfrac{3}{4}\))2. 42 - (\(\dfrac{1}{2}\))2 : 2 - 2\(\dfrac{3}{4}\)
= \(\dfrac{3^2}{4^2}\).42 - \(\dfrac{1}{4}\) : 2 - 2\(\dfrac{3}{4}\)
= 9 - \(\dfrac{1}{8}\) - \(\dfrac{11}{4}\)
= \(\dfrac{72}{8}\) - \(\dfrac{1}{8}-\dfrac{22}{8}\)
= \(\dfrac{71}{8}\) - \(\dfrac{22}{8}\)
= \(\dfrac{49}{8}\)
2; (\(\dfrac{3}{5}\))2.52 - (2\(\dfrac{1}{4}\))3 : (\(\dfrac{3}{4}\))3 - 3
= \(\dfrac{9}{5^2}\).52 - (\(\dfrac{9}{4}\))3 : (\(\dfrac{3}{4}\))3 - 3
= 9 - (\(\dfrac{9}{4}\) : \(\dfrac{3}{4}\))3 - 3
= 9 - 33 - 3
= 9 - 27 - 3
= 9 - (27 + 3)
= 9 - 30
= - 21

a: ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔAMO vuông tại M và ΔANO vuông tại N có
AO chung
AM=AN
Do đó: ΔAMO=ΔANO
b: O nằm trên đường trung trực của AB
=>OA=OB
O nằm trên đường trung trực của AC
=>OA=OC
Do đó: OA=OB=OC
c: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
=>\(\widehat{BAO}=\widehat{CAO}\)
=>AO là phân giác của góc BAC
d: Ta có: \(\widehat{IBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ICB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
=>I nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,I thẳng hàng
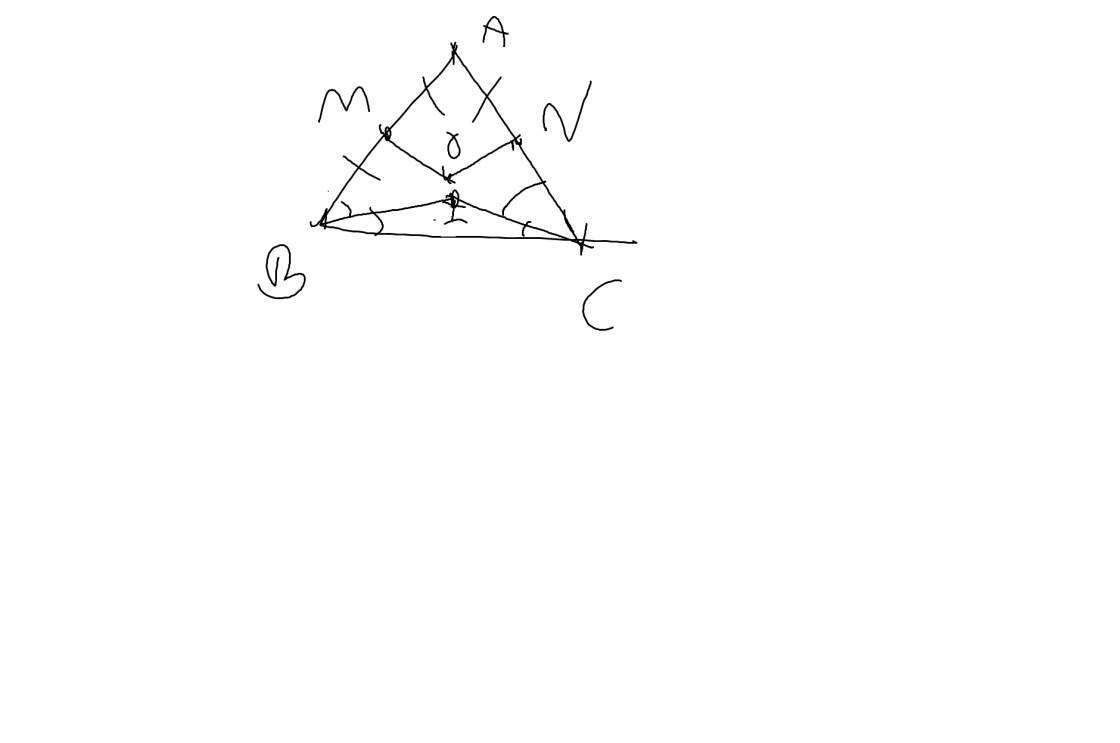

a: Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
=>\(GB=\dfrac{2}{3}BM;CG=\dfrac{2}{3}CN\)
mà BM=CN
nên GB=GC
b: Sửa đề: Chứng minh ΔBGN=ΔCOM
Ta có: GB+GM=BM
GC+GN=CN
mà BM=CN và GB=GC
nên GM=GN
Xét ΔGNB và ΔGMC có
GN=GM
\(\widehat{NGB}=\widehat{MGC}\)(hai góc đối đỉnh)
GB=GC
Do đó: ΔGNB=ΔGMC
c: ΔGNB=ΔGMC
=>NB=MC
mà \(NB=\dfrac{AB}{2};MC=\dfrac{AC}{2}\)
nên AB=AC
=>ΔABC cân tại A
d: Xét ΔABC có
AI,BM,CN là các đường trung tuyến
Do đó: AI,BM,CN đồng quy
vẽ hộ em bài này
4. (1,5 điểm) Cho ABC có hai đường trung tuyến BM và CN bằng nhau và cắt nhau tai G. a) Chứng minh GB = GC. b) Chứng minh BON = COM c) Chứng minh ABC cân, chỉ rõ cân tại đâu. d) Gọi I là trung điểm BC. Chứng minh AI, BM, CN đồng quy.

1: \(\dfrac{1}{2}-\left(\dfrac{2}{3}\right)^9:\left(\dfrac{2}{3}\right)^7+\dfrac{5}{6}\)
\(=\dfrac{1}{2}-\left(\dfrac{2}{3}\right)^2+\dfrac{5}{6}\)
\(=\dfrac{1}{2}-\dfrac{4}{9}+\dfrac{5}{6}\)
\(=\dfrac{9}{18}-\dfrac{8}{18}+\dfrac{15}{18}=\dfrac{16}{18}=\dfrac{8}{9}\)
2: \(\left(\dfrac{3}{7}\right)^3\cdot\left(\dfrac{7}{6}\right)^3+\dfrac{2}{3}:\left(\dfrac{4}{3}\right)^2\)
\(=\dfrac{1}{8}+\dfrac{2}{3}:\dfrac{16}{9}\)
\(=\dfrac{1}{8}+\dfrac{2}{3}\cdot\dfrac{9}{16}\)
\(=\dfrac{1}{8}+\dfrac{3}{8}=\dfrac{4}{8}=\dfrac{1}{2}\)
3: \(-\dfrac{4}{7}:\dfrac{9}{14}+\left(\dfrac{4}{3}\right)^4:\left(\dfrac{4}{3}\right)^2\)
\(=-\dfrac{4}{7}\cdot\dfrac{14}{9}+\left(\dfrac{4}{3}\right)^2\)
\(=-\dfrac{8}{9}+\dfrac{16}{9}=\dfrac{8}{9}\)
4: \(\left(-\dfrac{4}{3}+1\right)-\left(-\dfrac{2}{3}\right)^{21}:\left(-\dfrac{2}{3}\right)^{19}\)
\(=\dfrac{-1}{3}-\left(-\dfrac{2}{3}\right)^2\)
\(=-\dfrac{1}{3}-\dfrac{4}{9}=-\dfrac{7}{9}\)
5: \(\left(\dfrac{5}{2}-\dfrac{4}{3}\right)\cdot\dfrac{6}{7}+\left(-\dfrac{3}{2}\right)^5:\left(-\dfrac{3}{2}\right)^3\)
\(=\dfrac{15-8}{6}\cdot\dfrac{6}{7}+\left(-\dfrac{3}{2}\right)^2\)
\(=1+\dfrac{9}{4}=\dfrac{13}{4}\)
6: \(25^{10}\cdot\left(\dfrac{1}{5}\right)^{20}+\left(-\dfrac{3}{4}\right)^8\cdot\left(-\dfrac{4}{3}\right)^8-2011^0\)
\(=\dfrac{5^{20}}{5^{20}}+1-1=1+1-1=1\)
7: \(\left(\dfrac{3}{5}\right)^{10}\cdot\left(\dfrac{5}{3}\right)^{10}-\dfrac{13^4}{39^4}+2014^0\)
\(=\left(\dfrac{3}{5}\cdot\dfrac{5}{3}\right)^{10}-\dfrac{1}{3^4}+1\)
\(=1+1-\dfrac{1}{81}=2-\dfrac{1}{81}=\dfrac{161}{81}\)
8: \(\left(-0,5\right)^5:\left(-0,5\right)^3-\left(\dfrac{17}{2}\right)^7:\left(\dfrac{17}{2}\right)^6\)
\(=\left(-0,5\right)^2-\dfrac{17}{2}\)
\(=\dfrac{1}{4}-\dfrac{17}{2}=\dfrac{1}{4}-\dfrac{34}{4}=-\dfrac{33}{4}\)

a: ta có: \(\widehat{ABD}=\widehat{CBD}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\widehat{BCE}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{CBD}=\widehat{ACE}=\widehat{BCE}\)
Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
=>OB=OC

\(A\left(x\right)=x^{15}+5x^{14}+3x^3-24\)
\(=x^{14}\left(x+5\right)+3x^3+375-399\)
\(=3\left(x^3+125\right)-399\)
\(=3\left(x+5\right)\left(x^2-5x+25\right)-399\)
=-399
\(B\left(x\right)=\left(x^{2024}+7x^{2023}+1\right)^{2024}\)
\(=\left[x^{2023}\left(x+7\right)+1\right]^{2024}\)
\(=\left[x^{2023}\left(-7+7\right)+1\right]^{2024}=1^{2024}=1\)

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>BA=BE
b: Ta có: \(\widehat{EDC}+\widehat{ACB}=90^0\)(ΔECD vuông tại E)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{EDC}=\widehat{ABC}\)
Xét ΔABC có AB<AC
mà \(\widehat{ACB};\widehat{ABC}\) lần lượt là góc đối diện của các cạnh AB,AC
nên \(\widehat{ACB}< \widehat{ABC}\)
=>\(\widehat{ECD}< \widehat{EDC}\)
=>ED<EC
mà ED=DA và EC=AM
nên DA<AM<DM

\(6x^3+5x^2-3x+a\)
\(=6x^3-3x^2+8x^2-4x+x-\dfrac{1}{2}+a+\dfrac{1}{2}\)
\(=3x^2\left(2x-1\right)+4x\left(2x-1\right)+\dfrac{1}{2}\left(2x-1\right)+\left(a+\dfrac{1}{2}\right)\)
\(=\left(2x-1\right)\left(3x^2+4x+\dfrac{1}{2}\right)+\left(a+\dfrac{1}{2}\right)\)
Để \(\left(6x^3+5x^2-3x+a\right)⋮\left(2x-1\right)\)
thì: \(a+\dfrac{1}{2}=0\Leftrightarrow a=-\dfrac{1}{2}\)

a: \(A\left(x\right)=x^3\left(x+2\right)-5x+9+2x^3\left(x-1\right)\)
\(=x^4+2x^3-5x+9+2x^4-2x^3\)
\(=3x^4-5x+9\)
\(=9-5x+3x^4\)
\(B\left(x\right)=2\left(x^2-3x+1\right)-\left(3x^4+2x^3-3x+4\right)\)
\(=2x^2-6x+2-3x^4-2x^3+3x-4\)
\(=-3x^4-2x^3+2x^2-3x-2\)
\(=-2-3x+2x^2-2x^3-3x^4\)
b: \(A\left(x\right)+B\left(x\right)\)
\(=3x^4-5x+9-3x^4-2x^3+2x^2-3x-2\)
\(=-2x^3+2x^2-8x+7\)
A(x)-B(x)
\(=3x^4-5x+9+3x^4+2x^3-2x^2+3x+2\)
\(=6x^4+2x^3-2x^2-2x+11\)
c: Đặt C(x)=0
=>\(-2x^3+2x^2-8x+7=0\)
=>\(x\simeq0,9\)
d: \(H\left(x\right)=A\left(x\right)+5x=3x^4-5x+9+5x=3x^4+9\)
mà \(3x^4+9>=9>0\forall x\)
nên H(x) vô nghiệm
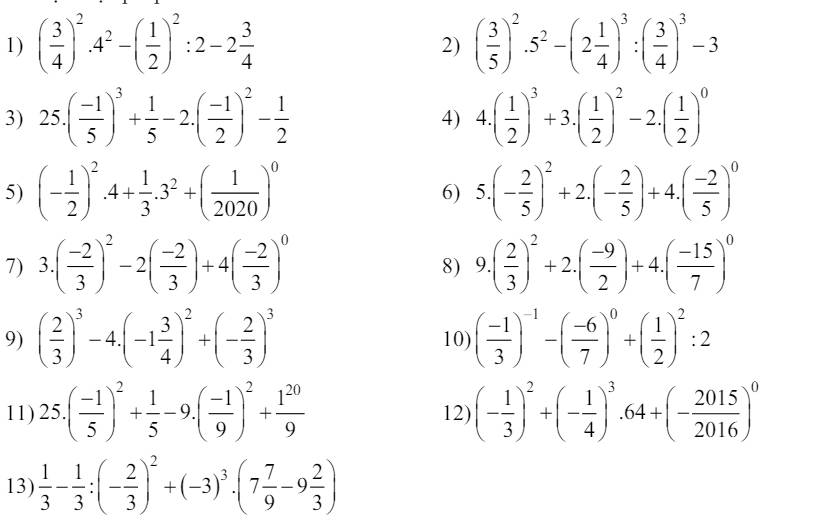
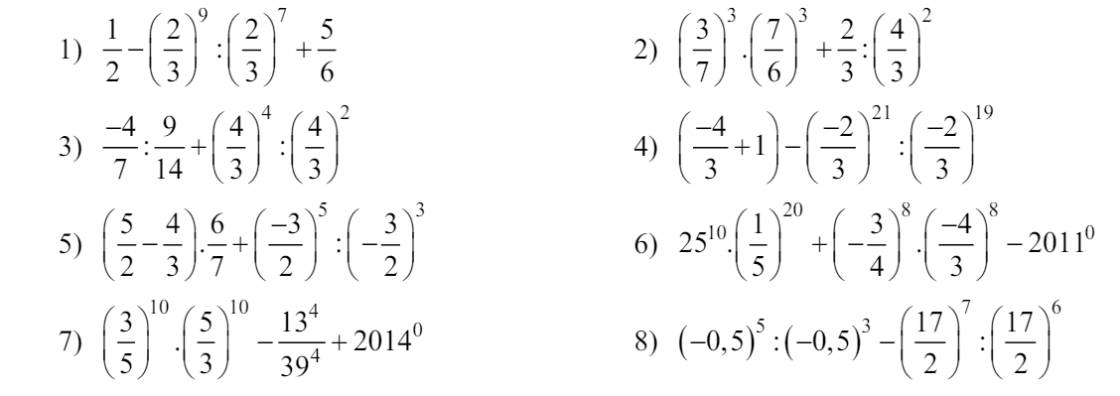

Gọi A là biến cố "Số ghi trên thẻ là số chia 6 dư 2"
=>A={2;8;14;20;26}
=>n(A)=5
\(P_A=\dfrac{5}{30}=\dfrac{1}{6}\)