Biểu đồ bên dưới thống kê số học sinh của mỗi khối lớp tham gia Câu lạc bộ STEM của một trường tiểu học. Biết tổng số học sinh tham gia Câu lạc bộ STEM là 60 học sinh.
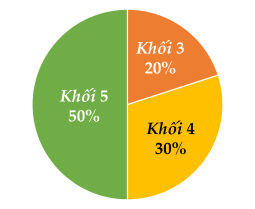
Có bao nhiêu học sinh Khối lớp 4 tham gia Câu lạc bộ STEM?
18 học sinh. 24 học sinh. 12 học sinh. 30 học sinh.
Giải:
Số học sinh khối 4 tham gia câu lạc bộ là:
60 x 30 : 100 = 18 (học sinh)
Chọn 18 học sinh