Cho \(b^2\)=ac; \(c^2\) =bd(a,b,c,d khác 0). CMR: \(\left(\dfrac{12a+3b-5c}{12b+3c-5d}\right)^3=\dfrac{a}{d}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mẹ là cái cung tên,con là cái mũi tên.Thấy đúng thì tick cho mình nhé các bạn.

Ta có: \(\dfrac{a}{12}=\dfrac{1}{3}\\ \Rightarrow a=\dfrac{12}{3}=4\)
Vậy \(a=4\).

\(\left(\dfrac{1}{9}\right)^5=\left[\left(\dfrac{1}{3}\right)^2\right]^5=\left(\dfrac{1}{3}\right)^{10}\)
\(\left(\dfrac{1}{27}\right)^7=\left[\left(\dfrac{1}{3}\right)^3\right]^7=\left(\dfrac{1}{3}\right)^{21}\)

** Bổ sung điều kiện $a,b,c>0$.
Áp dụng BĐT Cô-si cho các số dương:
$(a+b)(b+2c)(c+4a)=(a+\frac{b}{2}+\frac{b}{2})(b+c+c)(c+2a+2a)$
$\geq 3\sqrt[3]{a.\frac{b}{2}.\frac{b}{2}}.3\sqrt[3]{bc^2}.3\sqrt[3]{c.2a.2a}=27abc$
Ta có đpcm
Dấu "=" xảy ra khi $b=c=2a$

a: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
b: Xét ΔCAB vuông tại A và ΔCAE vuông tại A có
CA chung
AB=AE
Do đó: ΔCAB=ΔCAE
=>\(\widehat{ACB}=\widehat{ACE}\)
=>CA là phân giác của góc ECB

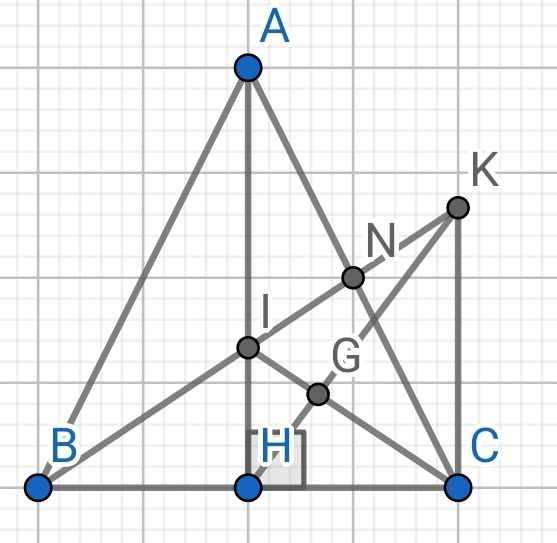
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét hai tam giác vuông: ∆AHB và ∆AHC có:
AH là cạnh chung
AB = AC (cmt)
⇒ ∆AHB = ∆AHC (cạnh huyền - cạnh góc vuông)
b) Do BN là đường trung tuyến của ∆ABC (gt)
⇒ N là trung điểm của AC
⇒ AN = CN
Do AH // CK (gt)
⇒ ∠IAN = ∠KCN (so le trong)
Xét ∆AIN và ∆CKN có:
∠ANI = ∠CNK (đối đỉnh)
AN = CN (cmt)
∠IAN = ∠KCN (cmt)
⇒ ∆AIN = ∆CKN (g-c-g)
⇒ NI = NK (hai cạnh tương ứng)
c) Xem lại đề. Em viết sai tùm lum

Ta thấy: \(\left\{{}\begin{matrix}\left(3x-2\right)^{2022}\ge0;\forall x\\\left(5y+4\right)^{2024}\ge0;\forall y\end{matrix}\right.\)
\(\Rightarrow\left(3x-2\right)^{2022}+\left(5y+4\right)^{2024}\ge0;\forall x,y\)
\(\Rightarrow\left(3x-2\right)^{2022}+\left(5y+4\right)^{2024}+2023\ge2023;\forall x,y\)
\(\Rightarrow C\ge2023;\forall x,y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}3x-2=0\\5y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-\dfrac{4}{5}\end{matrix}\right.\)
Vậy \(C_{min}=2023\) tại \(x=\dfrac{2}{3};y=-\dfrac{4}{5}\).

Sửa đề: \(\left(4x^4+14x^3-21x-9\right):\left(2x^2-3\right)\)
\(=\left(4x^4+14x^3+6x^2-6x^2-21x-9\right):\left(2x^2-3\right)\)
\(=\left[\left(4x^4-6x^2\right)+\left(14x^3-21x\right)+\left(6x^2-9\right)\right]:\left(2x^2-3\right)\)
\(=\left[2x^2.\left(2x^2-3\right)+7x.\left(2x^2-3\right)+3.\left(2x^2-3\right)\right]:\left(2x^2-3\right)\)
\(=\left(2x^2+7x+3\right).\left(2x^2-3\right):\left(2x^2-3\right)\)
\(=2x^2+7x+3\)
___________________
\(\left(6x^3-2x^2-9x+3\right):\left(3x-1\right)\)
\(=\left[\left(6x^3-2x^2\right)-\left(9x-3\right)\right]:\left(3x-1\right)\)
\(=\left[2x^2.\left(3x-1\right)-3.\left(3x-1\right)\right]:\left(3x-1\right)\)
\(=\left(2x^2-3\right).\left(3x-1\right):\left(3x-1\right)\)
\(=2x^2-3\)
`#NqHahh`
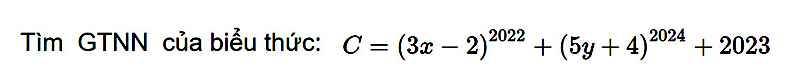
\(b^2=ac\)
=>\(\dfrac{c}{b}=\dfrac{b}{a}\)
\(c^2=bd\)
=>\(\dfrac{c}{b}=\dfrac{d}{c}\)
=>\(\dfrac{b}{a}=\dfrac{c}{b}=\dfrac{d}{c}\)
=>\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\)
=>\(\left\{{}\begin{matrix}c=dk\\b=ck=dk^2\\a=bk=dk^3\end{matrix}\right.\)
\(\left(\dfrac{12a+3b-5c}{12b+3c-5d}\right)^3=\left(\dfrac{12\cdot dk^3+3\cdot dk^2-5\cdot dk}{12\cdot dk^2+3\cdot dk-5d}\right)^3\)
\(=\left(\dfrac{k\left(12dk^2+3dk-5d\right)}{12dk^2+3dk-5d}\right)^3=k^3\)
\(\dfrac{a}{d}=\dfrac{dk^3}{d}=k^3\)
Do đó: \(\dfrac{a}{d}=\left(\dfrac{12a+3b-5c}{12b+3c-5d}\right)^3\)
cam on