Trên vỏ 1 cục pin có ghi 9V. Thông số này là:
A. Suất điện động của cục pin
B. Điện thế cực dương của pin
C. Hiệu điện thế giữa hai cực của pin
D. Điện thế cực âm của pin
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
13 tháng 10 2022
Câu 1 :
a) \(F=\dfrac{k.\left|q_1.q_2\right|}{r^2}=\dfrac{9.10^9.\left|2.10^{-5}.\left(-2.10^{-9}\right)\right|}{0,1^2}=0,036\)
b) 2 điện tích trái dấu nên đẩy nhau
13 tháng 10 2022
Bài 2 : ( chắc đề viết thiếu ở chỗ điện tích )
\(E=\dfrac{F}{q}\)
\(\Rightarrow F=E.q=2.10^3.2.10=40000\)
Bài 3 : xin thôi =))
Bài 4 :
Điện dung của tụ là :
\(Q=C.U\)
\(\Rightarrow C=\dfrac{Q}{U}=\dfrac{2.10^{-6}}{100}=2.10^{-8}\)
S
mọi người giúp em ý 2 với ạ
1
19 tháng 7 2022
Bài 6. Ý 2:
Lực tác dụng: \(F=BIl=0,4\cdot sin\alpha=0,4\cdot sin30^o=0,2N\)
\(P=m\cdot g=0,01\cdot10=0,1N\)
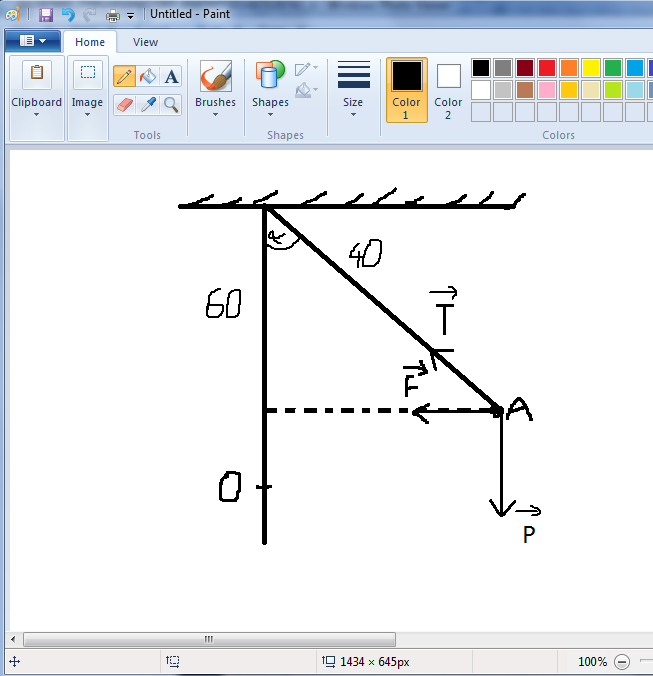
Giả sử O là vị trí thấp nhất.
Độ cao của dây MN so với O: \(h=l\cdot\left(1-cos\alpha\right)=60\cdot\left(1-cos30^o\right)=0,08m\)
Bảo toàn năng lượng:
\(W_O=W_A\Rightarrow\dfrac{1}{2}mv^2=mgh\Rightarrow v=\sqrt{2gl}=\sqrt{2\cdot10\cdot0,6}=2\sqrt{3}\)m/s
S
0
O
1
3 tháng 7 2022
Công thức lăng kính
\(sini_1=n.sinr_1;sini_2=n.sinr_2\\ A=r_1+r_2;D=I_1+I_2-A\)
Nếu các góc i và A nhỏ
\(i_1=nr_1;i_2=nr_2\\ A=r_1+r_2;D=\left(n-1\right)A\)
Độ tụ của thấu kính
\(D=\dfrac{1}{f}=\left(n-1\right)\left(\dfrac{1}{R_1}+\dfrac{1}{R_2}\right)\)
Vị trí ảnh
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'};d=\dfrac{d'f}{d'-f}\\ f=\dfrac{dd'}{d+d'};d'=\dfrac{df}{d-f}\)
Số phóng đại ảnh
\(\left|k\right|=\dfrac{A'B'}{AB};k=-\dfrac{d'}{d}=\dfrac{f}{f-d}=\dfrac{f-d'}{f}\)
Hệ 2 thấu kính đồng trục ghép sát
\(\dfrac{1}{f}=\dfrac{1}{f_1}+\dfrac{1}{f_2};D=D_1+D_2\)
Hệ 2 thấu kính đồng trục ghép cách nhau
- Quan hệ giữa 2 vai trò ảnh và vật của \(A_1'B_1'\)
\(AB\underrightarrow{L_1}A_1'B_1'\underrightarrow{L_2}A_2'B_2'\)
d_1 - d_1' ; d_2 - d_2'
Số phóng đại ảnh sau cùng
\(k=k_1k_2\)
Số bội giác
\(G=\dfrac{\alpha}{\alpha_o}\approx\dfrac{tan\alpha}{tan\alpha_o}\)
Kính lúp : ngắm chừng ở vô cực
\(G_{\infty}=\dfrac{OC_c}{f}=\dfrac{Đ}{f}\)
Kính hiển vi : ngắm chừng ở vô cực
\(G_{\infty}=\left|k_1\right|G_2=\dfrac{\delta D}{f_1f_2}\)
Kính thiên văn : ngắm chừng ở vô cực
\(G_{\infty}=\dfrac{f_1}{f_2}\)
C