Bài 1. Cho tam giác ABC, góc ACB bằng . Gọi I là giao điểm của hai đường cao AD và BE.
a) Chứng minh CI vuông góc với AB. b) Tính số đo góc BID và góc EID. Bài này làm kiểu j ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu đề cho là tuần đầu tiên người đó xử lí \(\dfrac{1}{4}\) số báo cáo và tuần tiếp xử lí được \(\dfrac{1}{2}\) số báo cáo thì làm như sau:
Giải:
Số báo cáo người đó còn phải xử lí sau hai tuần ứng với phân số là:
1 - \(\dfrac{1}{4}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{4}\) (số báo cáo)
Sau hai tuần, số báo cáo mà người đó còn phải xử là:
120 x \(\dfrac{1}{4}\) = 30 (báo cáo)
Đáp số: 30 báo cáo.
Nguyễn thị thương hoài .sau tuần 1 làm gì còn 120 báo cáo nữa cô ơi.

K thuộc SC nên (KBC) cũng là (SBC)
Từ A kẻ \(AH\perp SB\) (H thuộc SB)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AH\)
\(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(KBC\right)\right)=\dfrac{a}{\sqrt{2}}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow SA=\dfrac{AH.AB}{\sqrt{AB^2-AH^2}}=a\)
(tới đây nếu sử dụng kiến thức 12 tọa độ hóa thì bài toán được giải quyết nhanh gọn, còn làm kiểu hình thuần 11 hơi dài)
\(\Rightarrow SA=AB\Rightarrow\Delta SAB\) cân tại A \(\Rightarrow AH\) đồng thời là trung tuyến \(\Rightarrow G\) thuộc AH
\(\Rightarrow\left(AGK\right)\) trùng mặt phẳng \(\left(AHK\right)\)
Trong mp (SBC), nối HK cắt BC kéo dài tại E
\(\Rightarrow AE=\left(ABC\right)\cap\left(AGK\right)\) (1)
Theo cmt \(AH\perp\left(SBC\right)\Rightarrow AH\perp SC\Rightarrow SC\perp\left(AGK\right)\Rightarrow SC\perp AE\)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AE\)
\(\Rightarrow AE\perp\left(SAC\right)\) (2)
(1);(2) \(\Rightarrow\widehat{CAK}\) là góc giữa (ABC) và (AGK)
Hệ thức lượng: \(AK=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a\sqrt{6}}{3}\)
\(\Rightarrow cos\widehat{CAK}=\dfrac{AK}{AC}=\dfrac{\sqrt{3}}{3}\)

A = \(\dfrac{3n+2}{7n+1}\) (n \(\in\) N)
Gọi ƯCLN(3n + 2; 7n + 1) = d
Ta có: \(\left\{{}\begin{matrix}\left(3n+2\right).7⋮d\\\left(7n+1\right).3⋮d\end{matrix}\right.\)
\(\left\{{}\begin{matrix}21n+14⋮d\\21n+3⋮d\end{matrix}\right.\)
\(\left\{{}\begin{matrix}21n+14⋮d\\21n+14-21n-3⋮d\end{matrix}\right.\)
\(\left\{{}\begin{matrix}21n+14⋮d\\11⋮d\end{matrix}\right.\)
d \(\in\) Ư(11) = {1; 11}
\(\left\{{}\begin{matrix}3n+2⋮11\\7n+1⋮11\end{matrix}\right.\)
\(\left\{{}\begin{matrix}3n+2⋮11\\2.\left(3n+2\right)+n-3⋮11\end{matrix}\right.\)
n - 3 ⋮ 11
A = \(\dfrac{3n+2}{7n+1}\) tối giản khi và chỉ khi n - 3 \(\ne\) 11k (k \(\in\) N)
n \(\ne\) 11k + 3 (k \(\in\) N)

Gọi x (km) là độ dài quãng đường AB (x > 0)
Thời gian đi từ A đến B: x/45 (h)
Vận tốc lúc về: 45 - 5 = 40 (km/h)
Thời gian lúc về: x/40 (h)
30 phút = 1/2 h
Theo đề bài, ta có phương trình:
x/40 - x/45 = 1/2
9x - 8x = 180
x = 180 (nhận)
Vậy quãng đường AB dài 180 km

Bài 1
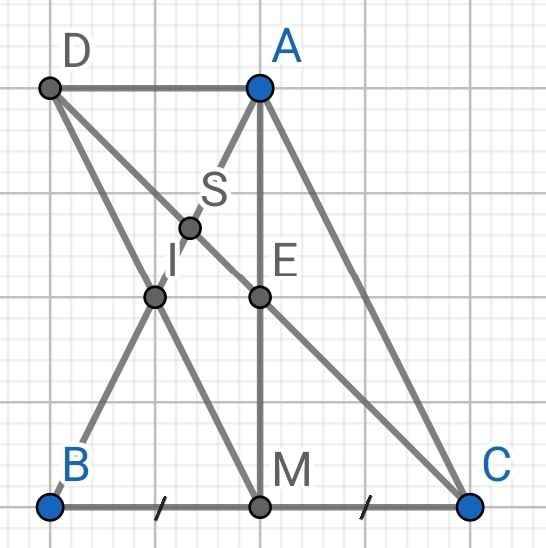
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Do M là trung điểm của BC (gt)
⇒ BM = MC
Xét ∆AMB và ∆AMC có:
AB = AC (cmt)
BC = MC (cmt)
AM là cạnh chung
⇒ ∆AMB = ∆AMC (c-c-c)
b) Do AD // BC (gt)
⇒ AD // BM
⇒ ∠DAI = ∠MBI (so le trong)
Xét ∆AID và ∆BIM có:
∠DAI = ∠MBI (cmt)
AI = BI (do I là trung điểm của AB)
∠AID = ∠BIM (đối đỉnh)
⇒ ∆AID = ∆BIM (g-c-g)
⇒ AD = BM (hai cạnh tương ứng)
Mà BM = MC (cmt)
⇒ AD = MC
c) ∆AMB = ∆AMC (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
⇒ ∠AMC = ∠EMC = 90⁰
⇒ ∆MCE vuông tại M
Mà AD // BC (cmt)
⇒ AD ⊥ AM
⇒ ∠DAM = ∠DAE = 90⁰
⇒ ∆ADE vuông tại A
Do AD // BC (gt)
⇒ ∠ADE = ∠MCE (so le trong)
Xét hai tam giác vuông: ∆ADE và ∆MCE có:
AD = MC (cmt)
∠ADE = ∠MCE (cmt)
⇒ ∆ADE = ∆MCE (cạnh góc vuông - góc nhọn kề)
⇒ AE = ME (hai cạnh tương ứng)
⇒ E là trung điểm của AM
Do ∆AID = ∆BIM (cmt)
⇒ ID = IM (hai cạnh tương ứng)
⇒ I là trung điểm của MD
∆ADM có:
AI là đường trung tuyến (do I là trung điểm của MD)
DE là đường trung tuyến (do E là trung điểm của AM)
Mà AI và DE cắt nhau tại S
⇒ S là trọng tâm của ∆ADE
⇒ AS = 2SI
⇒ 3AS = 6SI
Lại có:
AI = BI (cmt)
⇒ AB = AI + BI = 3SI + 3SI = 6SI
⇒ AB = 3AS
Mà AB > BC (gt)
⇒ 3AS > BC
Hay BC < 3AS
Bài 3
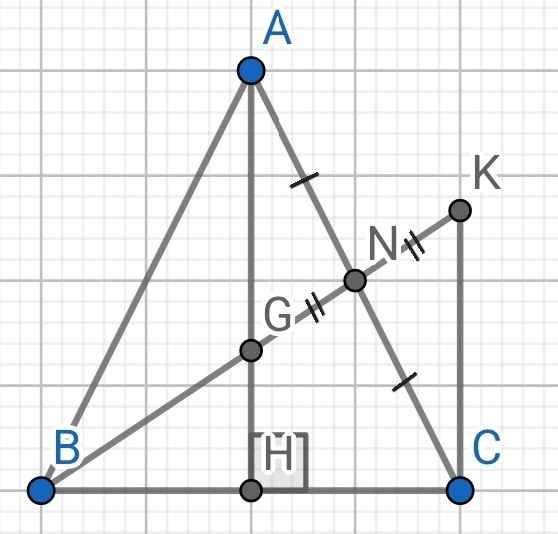
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét hai tam giác vuông: ∆ABH và ∆ACH có:
AB = AC (cmt)
AH là cạnh chung
⇒ ∆ABH = ∆ACH (cạnh huyền - cạnh góc vuông)
b) ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH cũng là đường trung tuyến của ∆ABC
Lại có N là trung điểm của AC (gt)
⇒ BN là đường trung tuyến thứ hai của ∆ABC
Mà AH và BN cắt nhau tại G (gt)
⇒ G là trọng tâm của ∆ABC
Xét ∆ANG và ∆CNK có:
AN = CN (do N là trung điểm của AC)
∠ANG = ∠CNK (đối đỉnh)
NG = NK (gt)
⇒ ∆ANG = ∆CNK (c-g-c)
⇒ ∠AGN = ∠CKN (hai góc tương ứng)
Mà ∠AGN và ∠CKN là hai góc so le trong
⇒ AG // CK
c) Do G là trọng tâm của ∆ABC (cmt)
⇒ AG = 2GN
Lại có:
NG = NK (gt)
⇒ GK = 2GN
Mà BG = 2GN (cmt)
⇒ BG = GK
⇒ G là trung điểm của BK
Góc ACB bằng cái gì thế em?