4 4 4=10 làm sao giải đây, có ai giúp tôi không
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) -0,257 + 0,019
= -0,238 ≃ -0,24
b) 2,13 - 2,16 x 0,2
= 2,13 - 0,432
= 1,698 ≃ 1,7
c) 1,213 + 1,18 : (-0,2)
= 1,213 + 1,18 x (-5)
= 1,213 - 5,9
= -4,687 ≃ -4,69

\(A=2^2+2^4+2^6+...+2^{200}\\ 2^2A=2^4+2^6+...+2^{202}\\ 4A-A=\left(2^4+2^6+2^8+...+2^{202}\right)-\left(2^2+2^4+2^6+...+2^{200}\right)\\ 3A=2^{202}-2^2\)
\(=>3A+4=2^{202}-2^2+4=2^{202}-4+4=2^{202}\)
\(=>2^{202}=4^n\\ =>2^{202}=\left(2^2\right)^n\\ =>2^{202}=2^{2n}\\ =>2n=202\\ =>n=101\)

\(42\cdot136+272\cdot15+28\cdot68\cdot2\)
\(=42\cdot136+30\cdot136+28\cdot136\)
\(=136\left(42+30+28\right)\)
\(=136\cdot100=13600\)
42 x 136 + 272 x 15 + 28 x 68 x 2
= 21 x (2 x 136) + 272 x 15 + (68 x 4) x 7 x 2
= 21 x 272 + 272 x 15 + 272 x 14
= 272 x (21 + 15 + 14)
= 272 x 50
= 13600

Tỉ số giữa Số học sinh khá và cả lớp là:
\(\dfrac{1}{2}\left(1-\dfrac{1}{4}\right)=\dfrac{1}{2}\cdot\dfrac{3}{4}=\dfrac{3}{8}\)
Số học sinh trung bình chiếm: \(1-\dfrac{3}{8}-\dfrac{1}{4}=\dfrac{5}{8}-\dfrac{2}{8}=\dfrac{3}{8}\)(số học sinh cả lớp)
Số học sinh cả lớp là \(24:\dfrac{3}{8}=24\cdot\dfrac{8}{3}=64\left(bạn\right)\)

\(4-\dfrac{2+\dfrac{1}{2}}{2-\dfrac{1}{2}}\\ =4-\dfrac{\dfrac{4}{2}+\dfrac{1}{2}}{\dfrac{4}{2}-\dfrac{1}{2}}\\ =4-\dfrac{5}{2}:\dfrac{3}{2}\\ =4-\dfrac{5}{3}\\ =\dfrac{12}{3}-\dfrac{5}{3}\\ =\dfrac{7}{3}\)
\(4-\dfrac{2+\dfrac{1}{2}}{2-\dfrac{1}{2}}=4-\dfrac{\dfrac{5}{2}}{\dfrac{3}{2}}\)
\(=4-\dfrac{5}{2}:\dfrac{3}{2}=4-\dfrac{5}{2}\cdot\dfrac{2}{3}\)
\(=4-\dfrac{5}{3}=\dfrac{12}{3}-\dfrac{5}{3}=\dfrac{7}{3}\)

Số lượng số hạng:
(202 - 4) : 3 + 1= 67 (số hạng)
Tổng:
(202 + 4) x 67 : 2 = 6901
ĐS: ...

1: Sửa đề: Vẽ \(\widehat{x'Ay'}\) là góc đối đỉnh của góc xAy
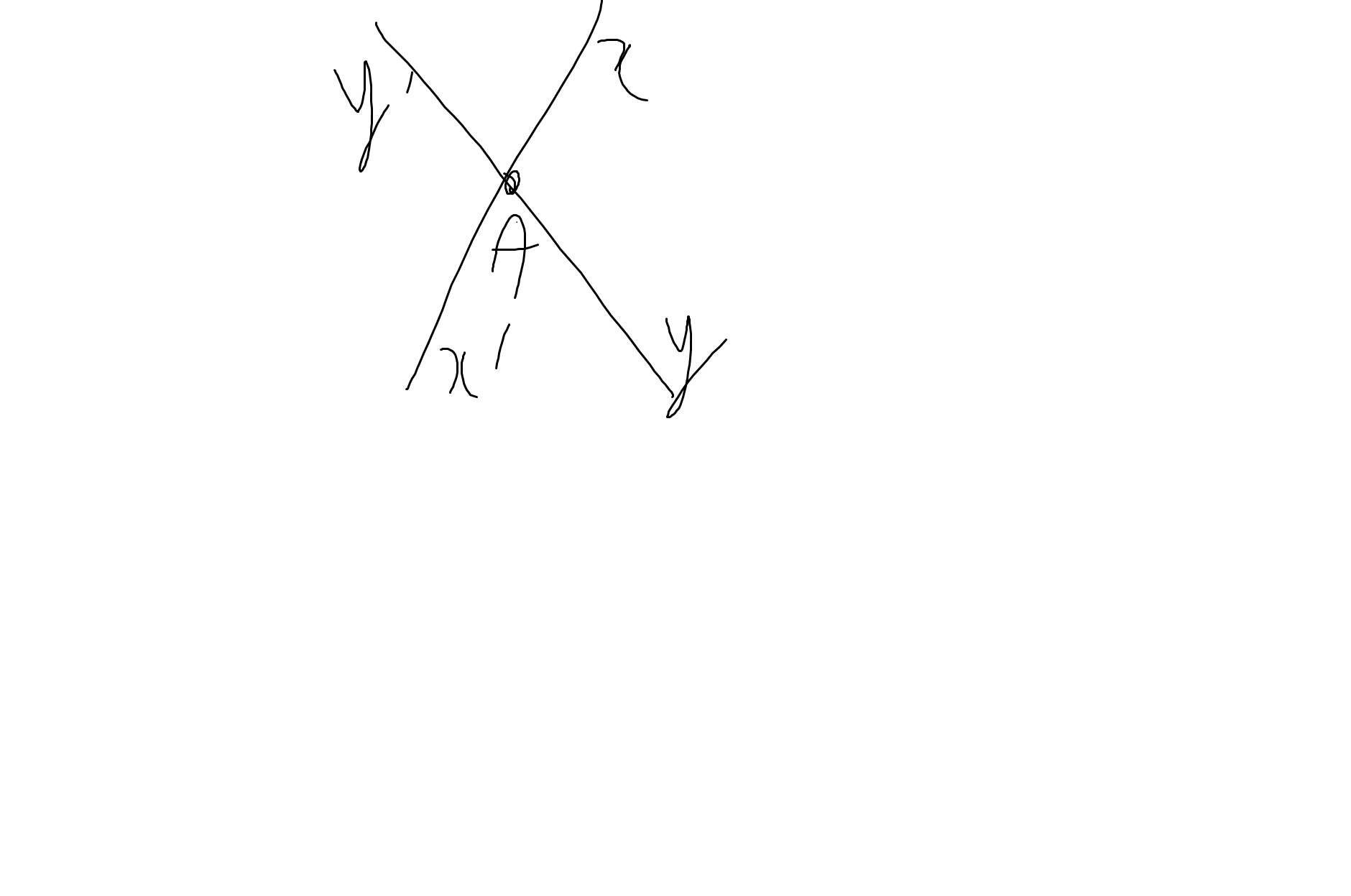
2: Ta có: \(\widehat{xAy}+\widehat{xAy'}=180^0\)(hai góc kề bù)
=>\(\widehat{xAy'}+100^0=180^0\)
=>\(\widehat{xAy'}=80^0\)
Ta có: \(\widehat{xAy}=\widehat{x'Ay'}\)(hai góc đối đỉnh)
mà \(\widehat{xAy}=100^0\)
nên \(\widehat{x'A'y}=100^0\)
Ta có: \(\widehat{xAy'}=\widehat{x'Ay}\)(hai góc đối đỉnh)
mà \(\widehat{xAy'}=80^0\)
nên \(\widehat{x'Ay}=80^0\)

a: Gọi số cần tìm có dạng là \(\overline{abc}\)
a có 8 cách chọn(Từ 1 đến 9, trừ số 5 ra)
b có 9 cách chọn(Từ 0 đến 9, loại số 5)
c có 9 cách chọn(Từ 0 đến 9, loại số 5)
Do đó: Có \(8\cdot9\cdot9=648\left(số\right)\)
b: Gọi số cần tìm có dạng là \(\overline{abc}\)
a có 9 cách chọn(Từ 1 đến 9)
b có 9 cách chọn(Từ 1 đến 9)
c có 9 cách chọn(Từ 1 đến 9)
Do đó: Có \(9\cdot9\cdot9=729\left(số\right)\)
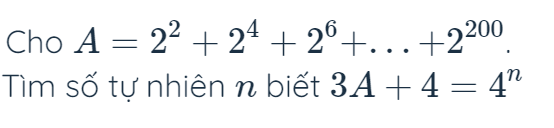
ủa 16-4=12, chứ đâu phải bằng 10 đâu