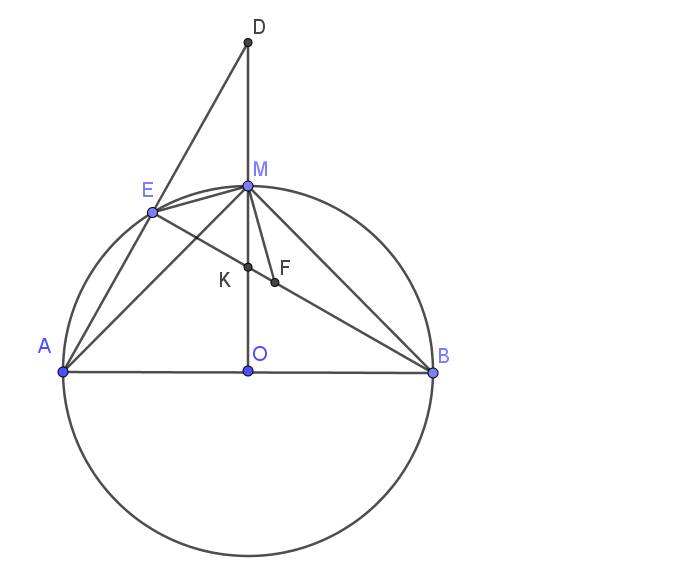
Cho điểm M nằm ngoài đường tròn (O; R). Qua M kẻ hai tiếp tuyến MA và MB và cát tuyến MCD(A, B, C, D
cùng thuộc đường tròn (O)), tia MC nằm giữa tia MO và MA. Gọi H là giao điểm của MO và AB.
a) Chứng minh tứ giác MAOB nội tiếp.
b) Gọi K là trung điểm của CD. Chứng minh 5 điểm M, K, A, O, B cùng thuộc một đường tròn. Suy ra KM

c) Đường thằng OK cắt đường thẳng AB tại N . Chứng minh ND là tiếp tuyến của đường tròn (O).
d) Vẽ đường kính BE của đường tròn (O). Từ C vẽ đường thẳng song song với OM cắt các đường thẳng BE
và ED lần lượt tại I, P . Chứng minh I là trung điểm CP .




a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
b: Ta có; ΔOCD cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)CD tại K
Ta có: \(\widehat{OKM}=\widehat{OAM}=\widehat{OBM}=90^0\)
=>O,K,A,M,B cùng thuộc đường tròn đường kính OM
c: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(2)
Từ (1),(2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H
Xét ΔOHN vuông tại H và ΔOKM vuông tại K có
\(\widehat{HON}\) chung
Do đó: ΔOHN~ΔOKM
=>\(\dfrac{OH}{OK}=\dfrac{ON}{OM}\)
=>\(OH\cdot OM=OK\cdot ON\left(3\right)\)
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2=R^2\left(4\right)\)
Từ (3),(4) suy ra \(OK\cdot ON=R^2=OD^2\)
=>\(\dfrac{OK}{OD}=\dfrac{OD}{ON}\)
Xét ΔOKD và ΔODN có
\(\dfrac{OK}{OD}=\dfrac{OD}{ON}\)
\(\widehat{KOD}\) chung
Do đó: ΔOKD~ΔODN
=>\(\widehat{OKD}=\widehat{ODN}=90^0\)
=>ND là tiếp tuyến của (O)