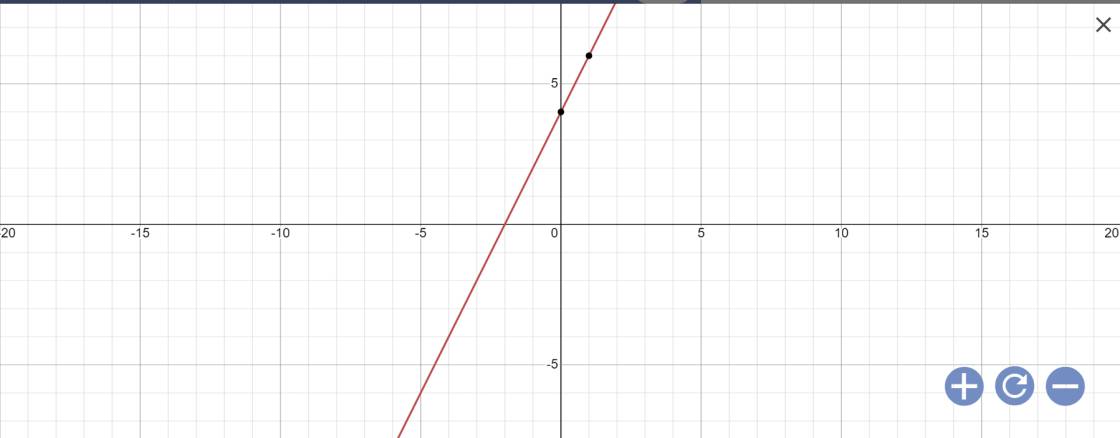
a, vẽ đồ thị hàm số y=2x+4/ b , tìm giá trị của m để đường thẳng y=(m+1)x+2 ( m khác -1) song song với đường thẳng y=-2x+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

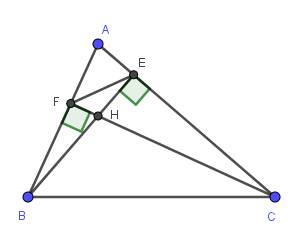
a) Xét hai tam giác vuông: \(\Delta BHF\) và \(\Delta CHE\) có:
\(\widehat{BHF}=\widehat{CHE}\) (đối đỉnh)
\(\Rightarrow\Delta BHF\) ∽ \(\Delta CHE\) (g-g)
\(\Rightarrow\dfrac{HB}{HC}=\dfrac{HF}{HE}\)
\(\Rightarrow HE.HB=HC.HF\)
b) Xét hai tam giác vuông: \(\Delta AFC\) và \(\Delta AEB\) có:
\(\widehat{A}\) chung
\(\Rightarrow\Delta AFC\) ∽ \(\Delta AEB\) (g-g)
\(\Rightarrow\dfrac{AF}{AE}=\dfrac{AC}{AB}\)
\(\Rightarrow\dfrac{AF}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ABC\) có:
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\) (cmt)
\(\widehat{A}\) chung
\(\Rightarrow\Delta AEF\) ∽ \(\Delta ABC\) (c-g-c)

MD là phân giác của góc NMP
=>\(\widehat{NMD}=\widehat{PMD}=\dfrac{\widehat{NMP}}{2}=45^0\)
Xét tứ giác EMDN có \(\widehat{EDN}=\widehat{EMN}=90^0\)
nên EMDN là tứ giác nội tiếp
=>\(\widehat{END}+\widehat{EMD}=180^0\)
=>\(\widehat{END}=\widehat{DMP}=45^0\)
Xét ΔDNE vuông tại D có \(\widehat{DNE}=45^0\)
nên ΔDNE vuông cân tại D

Lời giải:
Gọi chiều dài và chiều rộng hcn lớn lần lượt là $a$ cm và $b$ cm
Ta có: $a+b=100:2=50$
Khi chia hcn thành 1 hv và 1 hcn thì ta có 1 hình vuông cạnh $b$ cm và 1 hcn có độ dài 2 chiều là $b$ cm và $a-b$ cm
Chu vi hcn mới: $2(b+a-b)=60$
$\Leftrightarrow a=30$ (cm)
$b=50-a=50-30=20$ (cm)
Vậy độ dài cạnh hcn ban đầu là $20$ cm và $30$ cm

Bài 7:
a: Thay x=1 vào B, ta được:
\(B=\dfrac{2-1}{1}=\dfrac{1}{1}=1\)
b: \(A=\dfrac{1}{x-2}+\dfrac{2x}{x^2-4}+\dfrac{1}{x+2}\)
\(=\dfrac{1}{x-2}+\dfrac{2x}{\left(x-2\right)\left(x+2\right)}+\dfrac{1}{x+2}\)
\(=\dfrac{x+2+2x+x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x}{\left(x-2\right)\left(x+2\right)}\)
c: \(A\cdot B=1\)
=>\(\dfrac{4x}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{2-x}{x}=1\)
=>\(\dfrac{-4}{x+2}=1\)
=>x+2=-4
=>x=-6(nhận)

Bài 2:
Gọi vận tốc xe 1 là x(km/h)
(Điều kiện: x>0)
vận tốc xe 2 là x+10(km/h)
Tổng vận tốc hai xe là 200:2=100(km/h)
=>x+x+10=100
=>2x=90
=>x=45(nhận)
vậy: vận tốc của xe 1 là 45km/h
vận tốc của xe 2 là 45+10=55km/h

Olm chào em, vấn đề em hỏi Olm xin hỗ trợ như sau:
Đoạn \(\dfrac{OA}{OC}\) = \(\dfrac{OB}{OD}\) (hệ quả của định lí Thales). Em hiểu rồi đúng chưa.
Từ dòng suy ra \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{OA+OC}{OB+OD}\) = \(\dfrac{AC}{BD}\) là em không hiểu tại sao phải không?
Vậy Olm sẽ giảng cho em như sau:
\(\dfrac{OA}{OC}\) = \(\dfrac{OB}{OD}\) (hệ quả định lí Thales) ⇒ \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) (tc tỉ lệ thức)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{OA+OC}{OB+OD}\) (1)
Mặt khác O là giao điểm của AC và BD nên
\(\left\{{}\begin{matrix}OA+OC=AC\\OB+OD=BD\end{matrix}\right.\) (2)
Thay (2) vào (1) ta có: \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{AC}{BD}\)
Giải thích đoạn: \(\dfrac{AO}{AC}\) = \(\dfrac{BO}{BD}\)
\(\dfrac{OA}{OB}\) = \(\dfrac{AC}{BD}\) (cmt) ⇒\(\dfrac{AO}{BO}=\dfrac{AC}{BD}\) ⇒ \(\dfrac{AO}{AC}\) = \(\dfrac{BO}{BD}\) (tính chất tỉ lệ thức)
Mọi chi tiết bài giảng liên hệ zalo 0385 168 017

Bước 1: Tìm số hạng tổng quát của mỗi cấp số nhân
Số hạng tổng quát:
aₙ = a₁ * r₁^(n-1) = 1 * 1.51^(n-1)Số hạng tổng quát:
aₙ = a₁ * r₂^(n-1) = 1 * 2.52^(n-1)Bước 2: Tính tổng n số hạng đầu tiên của mỗi cấp số nhân
Bước 3: Đặt S₁ = S₂ và giải phương trình
1 * (1 - 1.51^n) / (1 - 1.51) = 1 * (1 - 2.52^n) / (1 - 2.52) (1 - 1.51^n) / (1 - 1.51) = (1 - 2.52^n) / (1 - 2.52)Nhân chéo:
(1 - 1.51^n) * (1 - 2.52) = (1 - 2.52^n) * (1 - 1.51) 1 - 2.52 + 2.52 * 1.51^n = 1 - 1.51 + 1.51 * 2.52^n 1.51 * 2.52^n - 1.51 * 1.51^n = 1 - 2.52 1.51^n * (2.52 - 1.51) = 1 - 2.52 1.51^n = (1 - 2.52) / (2.52 - 1.51) 1.51^n = -1.52 / 1.01Lấy logarit cơ số 1.51 của cả hai vế:
n * log₁.₅₁(-1.52 / 1.01) = log₁.₅₁(-1.52 / 1.01) n = log₁.₅₁(-1.52 / 1.01) / log₁.₅₁(-1.52 / 1.01) n = 1Vậy, n = 1.

(2x - 1)/3 -(x +2)/6 =5
2(2x - 1)/6 - (x+2)/6 = (5 .6)/6
4x -2 -x -2 = 30
3x = 34
x = 34/3

Đường thẳng y=x-4 có a=1>0
nên đường thẳng y=x-4 tạo với trục Ox một góc nhọn có số đo là:
\(arctan\left(1\right)=45^0\)
b: Để đường thẳng y=(m+1)x+2 song song với đường thẳng y=-2x+1 thì \(\left\{{}\begin{matrix}m+1=-2\\2\ne1\left(đúng\right)\end{matrix}\right.\)
=>m+1=-2
=>m=-3
a: