Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔAHB vuông tại H và ΔAHD vuông tại H có
AH chung
HB=HD
Do đó: ΔAHB=ΔAHD
b: \(\widehat{BAH}+\widehat{ABC}=90^0\)(ΔHBA vuông tại H)
\(\widehat{ACB}+\widehat{ABC}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{BAH}=\widehat{ACB}\)
a) xét ΔAHB và ΔAHD, có:
AH là cạnh chung
\(\widehat{BHA}=\widehat{DHA}=90^0\)
HB = HD (giả thiết)
-> ΔAHB = ΔAHD (c-g-c)
b) xét ΔBHA có:
\(\widehat{HAB}=\widehat{BHA}-\widehat{B}\) (1)
xét ΔACB có:
\(\widehat{BCA}=\widehat{BAC}-\widehat{B}\) (2)
từ (1) (2) => \(\widehat{BAH}=\widehat{ACB}\) (vì \(\widehat{BHA}=\widehat{BAC}\))
c) trên đề ghi là điểm F mà xuống câu c thì lại là điểm E, vậy thì điểm F và điểm E là như nhau nghen
ta có: \(\widehat{HAD}=\widehat{AHD}-\widehat{HDA}\)
\(\widehat{FCD}=\widehat{DFC}-\widehat{FDC}\)
mà \(\widehat{AHD}=\widehat{CFD}=90^0\)
\(\widehat{HDA}=\widehat{FDC}\left(dd\right)\)
\(\Rightarrow\widehat{HAD}=\widehat{FCD}\) (3)
vì ΔHAB = ΔHAD (câu a), nên \(\widehat{HAB}=\widehat{HAD}\) (2 góc tương ứng) (4)
mà \(\widehat{HAB}=\widehat{HCA}\) (câu b) (5)
từ (3) (4) (5) => \(\widehat{DCA}=\widehat{DCF}\)
=> CB là tia phân giác của góc ACF
d) vì góc DAC = góc DCA nên tam giác DAC là tam giác cân
=> DA = DC
xét tam giác VUÔNG HDA và tam giác VUÔNG FDC, có:
DA = DC (cmt) (8)
góc HDA = góc FDC (đối đỉnh)
=> tam giác HDA = tam giác FDC (ch-gn)
=> DH = DF (6)
vì góc HAC = góc FCA , nên tam giác AKC là tam giác cân
=> KA = KC (7)
từ (6) (7) (8) => KD là đường trung trực của tam giá KAC
=> KD vuông góc với AC
mà AB vuông góc với AC
nên KD // AB (đpcm)
e) xét tam giác AFC có góc F là góc vuông
=> AC là cạnh lớn nhất
=> AC > CD
a:
Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
=>ΔAEF cân tại A
a: \(-\dfrac{18}{31}=\dfrac{-18\cdot114}{31\cdot114}=-\dfrac{2052}{3534}\)
\(-\dfrac{23}{114}=\dfrac{-23\cdot31}{114\cdot31}=\dfrac{-713}{3534}\)
mà -2052<-713
nên \(-\dfrac{18}{31}< -\dfrac{23}{114}\)
b: \(\dfrac{-22}{35}=\dfrac{-22\cdot177}{35\cdot177}=\dfrac{-3894}{6195}\)
\(-\dfrac{103}{177}=\dfrac{-103\cdot35}{177\cdot35}=\dfrac{-3605}{3195}\)
mà -3894<-3605
nên \(-\dfrac{22}{35}< -\dfrac{103}{177}\)
hình như đề bị sai rồi
\(\widehat{CAB}=\widehat{ACM}\) không thể là trung điểm BC được
a: Sửa đề: M là trung điểm của BC
Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
=>ΔAEF cân tại A
Xét tam giác ABC:
góc B = góc C
=> tam giác ABC cân tại A
=> AB = AC
Bạn xem lại nhé CM AB=AC mới đúng nha
Ta có, tam giác ABC có góc B bằng góc C
=> Tam giác ABC cân tại A
=>AB=AC
Sửa đề: Tìm x, y nguyên
\(2xy+3y-2x=4\\\Rightarrow (2xy-2x)+(3y-3)=4-3\\\Rightarrow 2x(y-1)+3(y-1)=1\\\Rightarrow (2x+3)(y-1)=1\)
Vì x, y nguyên nên \(\)\(2x+3;y-1\) có giá trị nguyên
Mà \((2x+3)(y-1)=1\)
Do đó ta có bảng sau:
| 2x + 3 | 1 | -1 |
| y - 1 | 1 | -1 |
| x | -1 | -2 |
| y | 2 | 0 |
Vì x, y tìm được đều thoả mãn x, y nguyên nên \((x;y)=(-1;2);(-2;0)\)
$Toru$
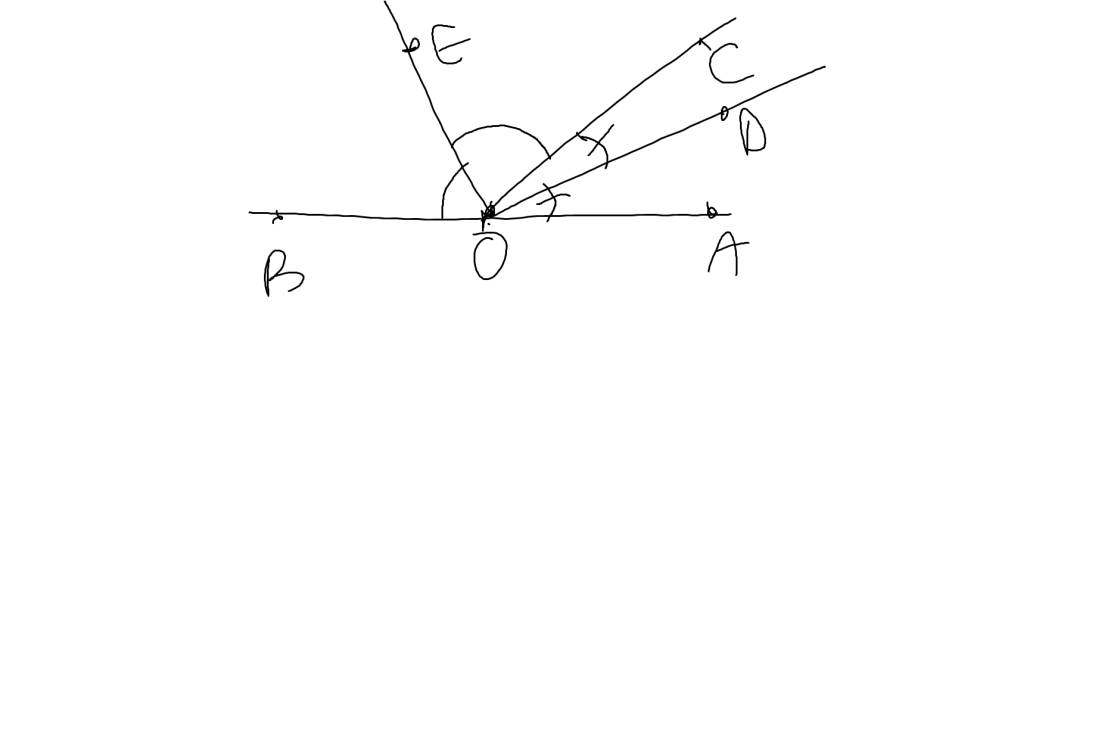
Gọi hai góc kề bù là góc AOC và góc BOC, gọi OD,OE lần lượt là phân giác của góc AOC và góc BOC
OD là phân giác của góc AOC
=>\(\widehat{AOC}=2\cdot\widehat{COD}\)
OE là phân giác của góc BOC
=>\(\widehat{BOC}=2\cdot\widehat{EOC}\)
Ta có: \(\widehat{AOC}+\widehat{BOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{COD}+\widehat{COE}\right)=180^0\)
=>\(2\cdot\widehat{DOE}=180^0\)
=>\(\widehat{DOE}=90^0\)
Đáp án là 6 giờ.
6giờ