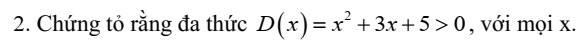
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ tia CxCx là tia phân giác của ˆACDACD^ và DyDy là tia phân giác của ˆBDCBDC^, hai tia CxCx và DyDy cắt nhau tại EE.
ˆC1=ˆC2=60∘C1^=C2^=60∘ và ˆD1=ˆD2=30∘D1^=D2^=30∘
Kẻ tia Ez//m//nEz//m//n, tính ˆE1=60∘E1^=60∘ và ˆE2=30∘E2^=30∘
Suy ra ˆCED=90∘CED^=90∘.
Kẻ tia CxCx là tia phân giác của \widehat{A C D}ACD và DyDy là tia phân giác của \widehat{B D C}BDC, hai tia CxCx và DyDy cắt nhau tại EE.
\widehat{C_1}=\widehat{C_2}=60^{\circ}C1=C2=60∘ và \widehat{D_1}=\widehat{D_2}=30^{\circ}D1=D2=30∘
Kẻ tia Ez / / m // nEz//m //n, tính \widehat{E_1}=60^{\circ}E1=60∘ và \widehat{E_2}=30^{\circ}E2=30∘
Suy ra \widehat{CED}=90^{\circ}CED=90∘.

\(a)\hept{\begin{cases}\text{Ta có:}\widehat{A_4}=\widehat{B_2}=110^0\\\text{Mà chúng so le trong}\end{cases}}\)
\(\Rightarrow a//b\)
\(b)\hept{\begin{cases}\text{Ta có:}c\perp a\left(gt\right)\\\text{Mà }a//b\left(cmt\right)\end{cases}}\)
\(\Rightarrow c\perp b\)
\(c)\text{Ta có:}\widehat{B_1}+\widehat{B_2}=180^0\left(\text{kề bù}\right)\)
\(\Rightarrow\widehat{B_1}=180^0-\widehat{B_2}\)
\(\Rightarrow\widehat{B_1}=180^0-110^0=70^0\)
\(\text{Ta có:}\widehat{B_1}=\widehat{B_3}=70^0\left(\text{đối đỉnh}\right)\)
\(\text{Ta có:}\widehat{B_3}=\widehat{C_3}\left(\text{Đồng vị}\right)\)
\(\Rightarrow\widehat{B_3}=\widehat{C_3}=70^0\)
a) Ta có: {ˆA4=110∘ˆB2=110∘⇒ˆA4=ˆB2=110∘{A4^=110∘B2^=110∘⇒A4^=B2^=110∘.
Mà hai góc ờ vị trí so le trong ⇒⇒ a//ba//b.
b) Ta có: {c⊥aa//b⇒c⊥b{c⊥aa//b⇒c⊥b
c) Vì a//b⇒ˆA4+ˆB1=180∘a//b⇒A4^+B1^=180∘
Mà hai góc ở vị trí trong cùng phía ⇒ˆB1=180∘−ˆA4=70∘⇒B1^=180∘−A4^=70∘.
Vì b⊥cb⊥c; e⊥ce⊥c và b//eb//e
⇒ˆB2=ˆC2=110∘⇒B2^=C2^=110∘ (hai góc ở vị trí đồng vị)
Ta có ˆC2C2^ và ˆC3C3^ là hai góc kề bù ⇒ˆC2+ˆC3=180∘⇒C2^+C3^=180∘
⇒ˆC3=180∘−ˆC2=70∘⇒C3^=180∘−C2^=70∘.

\(\text{Cặp góc so le trong là:}\)
\(A_3\text{ và }B_1\)
\(A_4\text{ và }B_2\)
\(\text{Cặp góc đồng vị là:}\)
\(A_2\text{ và }B_2\)
\(A_3\text{ và }B_3\)
\(A_1\text{ và }B_1\)
\(A_4\text{ và }B_4\)

`Answer:`
\(\left|1-3x\right|=\left|2x+5\right|\)
\(\Leftrightarrow\left|-3x+1\right|=\left|2x+5\right|\)
\(\Leftrightarrow\orbr{\begin{cases}-3x+1=2x+5\\-3x+1=-\left(2x+5\right)\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}-3x+1-2x=2x+5-2x\\-3x+1=-2x-5\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}-5x+1=5\\-3x+1+2x=-2x-5+2x\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}-5x+1-1=5-1\\-x+1=-5\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}-5x=4\\-x=-6\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{4}{5}\\x=6\end{cases}}\)

A B C 5 cm 5 cm H
\(\text{Xét }\Delta ABH\text{ và }\Delta ACH\text{ có:}\)
\(AH\text{ chung}\)
\(\widehat{AHB}=\widehat{AHC}=90^0\left(gt\right)\)
\(AB=AC=5\left(cm\right)\left(gt\right)\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c-g-c\right)\)


`Answer:`
\(D\left(x\right)=x^2+3x+5\)
\(=x^2+3x+\frac{9}{4}+\frac{11}{4}\)
\(=\left(x+\frac{3}{2}\right)^2+\frac{11}{4}\)
Mà \(\left(x+\frac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow D\left(x\right)=\left(x+\frac{3}{2}\right)^2+\frac{11}{4}\ge\frac{11}{4}>0\)
Vậy `D(x)=x^2 +3x+5>0` với mọi `x`