Cho tam giác ABC, vẽ đường cao AH. Biết BH=4cm,HC=9cm. a/CM: tam giác HBA đồng dạng tam giác HCA. b/CM: góc HBA=góc HAC. c/CM: tam giác ABC vuông tại A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
6 tháng 5 2024
đề khó hiểu thế
nó có thanh công cụ mà bạn dùng nó mà viết đề
7 tháng 5 2024
Câu 1: C
Câu 2: D
Câu 3: A
Câu 4: B
Câu 5; D
Câu 6: B
Câu 7: D
Câu 8: A
Câu 9: B
Câu 10: A
Câu 11: D
Câu 12: C
Câu 13: B
Câu 14: A
Câu 15: A
Câu 16: B
Câu 17: C
Câu 18: B
Câu 19: C
7 tháng 5 2024
a: Xét ΔMPN có \(MN^2+MP^2=NP^2\)
nên ΔMNP vuông tại M
Xét ΔMNP có ND là phân giác
nên \(\dfrac{DM}{PD}=\dfrac{NM}{NP}=\dfrac{3}{5}\)
b: Xét ΔMND vuông tại M và ΔHND vuông tại H có
\(\widehat{MND}=\widehat{HND}\)
Do đó: ΔMND~ΔHND
Xét ΔPHD vuông tại H và ΔPMN vuông tại M có
\(\widehat{HPD}\) chung
Do đó; ΔPHD~ΔPMN
c: ΔPHD~ΔPMN
=>\(\dfrac{HD}{MN}=\dfrac{PD}{PN}\)
=>\(DH\cdot NP=MN\cdot PD\)
BG
2
TN
6 tháng 5 2024
Yêu cầu bạn sáng cao anh không trả lời lung tung!
6 tháng 5 2024
Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Độ dài quãng đường lúc về là x+10(km)
Thời gian đi là \(\dfrac{x}{45}\left(giờ\right)\)
Thời gian về là \(\dfrac{x+10}{50}\left(giờ\right)\)
Thời gian về ít hơn thời gian đi 30p=0,5 giờ nên ta có:
\(\dfrac{x}{45}-\dfrac{x+10}{50}=0,5\)
=>\(\dfrac{10x-9\left(x+10\right)}{450}=0,5\)
=>10x-9x-90=225
=>x-90=225
=>x=315(nhận)
vậy: Độ dài quãng đường AB là 315km
6 tháng 5 2024
a: Xét ΔAEH vuông tại E và ΔAHB vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔAHB
=>\(\dfrac{AE}{AH}=\dfrac{AH}{AB}\)
=>\(AE\cdot AB=AH^2\)
b: Xét ΔAFH vuông tại F và ΔAHC vuông tại H có
\(\widehat{FAH}\) chung
Do đó: ΔAFH~ΔAHC
=>\(\dfrac{AF}{AH}=\dfrac{AH}{AC}\)
=>\(AF\cdot AC=AH^2\)
=>\(AE\cdot AB=AF\cdot AC\)
=>\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
\(\widehat{EAF}\) chung
Do đó: ΔAEF~ΔACB
=>\(\widehat{AEF}=\widehat{ACB}\)
=>\(\widehat{MEB}=\widehat{MCF}\)
Xét ΔMEB và ΔMCF có
\(\widehat{MEB}=\widehat{MCF}\)
\(\widehat{EMB}\) chung
Do đó ΔMEB~ΔMCF
=>\(\dfrac{ME}{MC}=\dfrac{MB}{MF}\)
=>\(ME\cdot MF=MB\cdot MC\)
KV
6 tháng 5 2024
a) *) \(y=-3x\)
| \(x\) | \(1\) |
| \(y=-3x\) | \(-3\) |
*) \(y=2x+1\)
| \(x\) | \(0\) | \(-1\) |
| \(y=2x+1\) | \(1\) | \(-1\) |
* Đồ thị:
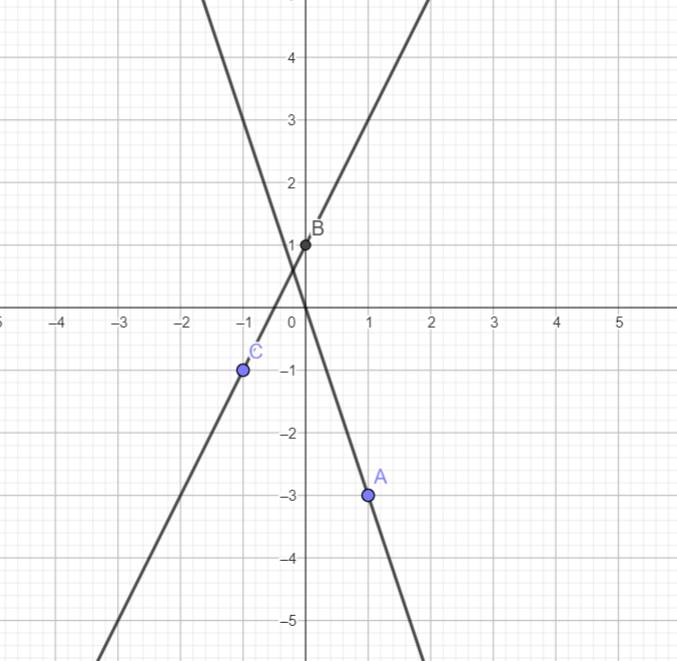
b) Phương trình hoành độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\):
\(-3x=2x+1\)
\(-3x-2x=1\)
\(-5x=1\)
\(x=-\dfrac{1}{5}\)
Thế \(x=-\dfrac{1}{5}\) vào \(\left(d_1\right)\) ta có:
\(y=-3.\left(\dfrac{-1}{5}\right)=\dfrac{3}{5}\)
Vậy tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\) là \(\left(\dfrac{-1}{5};\dfrac{3}{5}\right)\)