khối học sinh khối 6 của trường có khoảng 700 đến 1200 học sinh đi tham quan nếu 30 hay 45 học sinh lên 1 một xe thì thiếu 5 em còn xếp 43 học sinh lên xe thì vừa đủ . hỏi trường đó có bao nhiêu học sinh ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số đó có dạng \(\overline{ab}\)
Khi thêm số 0 vào giữa thì ta có số mới là: \(\overline{a0b}=100a+b\)
Mà số mới gấp 7 lần số cũ nên ta có:
\(\overline{a0b}=7\overline{ab}\\ 100a+b=7\left(10a+b\right)\\ 100a+b=70a+7b\\ 100a-70a=7b-b\\ a\left(100-70\right)=b\left(7-1\right)\\ 30a=6b\\ \dfrac{a}{b}=\dfrac{6}{30}=\dfrac{1}{5}\)
`=> a=1;b=5`
Vậy sso cần tìm là 15

câu b đề bài cho B < \(\dfrac{1}{3}\) thì cần gì chứng minh nữa em.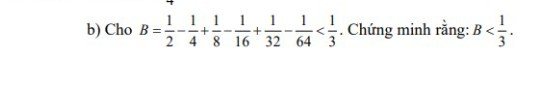
Đáng lẽ phải là: Cho B = \(\dfrac{1}{2}\) - \(\dfrac{1}{4}\) +...-\(\dfrac{1}{64}\)
Chứng minh B < \(\dfrac{1}{3}\)

`n^2+n+4` chia hết cho n + 1
`=>(n^2+n) +4` chia hết cho n + 1
`=> n(n+1)+4` chia hết cho n + 1
Mà: `n(n+1)` chia hết cho n + 1
=> 4 chia hết cho n + 1
=> n + 1 ∈ Ư(4) = {1; -1; 2; -2; 4; -4}
=> n ∈ {0; -2; 1; -3; 3; -5}

\(\left(27+11\right)\cdot\left(512-\left[14\cdot\left(64-4^2\right):2\right]\right)\\ =33\cdot\left[512-\left[14\cdot\left(64-16\right):2\right]\right]\\ =33\cdot\left(512-14\cdot48:2\right)\\ =33\cdot\left(512-14\cdot24\right)\\ =33\cdot\left(512-336\right)\\ =33\cdot176\\ =5808\)

\(C=\dfrac{9}{1\cdot2}+\dfrac{9}{2\cdot3}+...+\dfrac{9}{44\cdot45}\)
\(=9\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{44\cdot45}\right)\)
\(=9\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{44}-\dfrac{1}{45}\right)\)
\(=9\left(1-\dfrac{1}{45}\right)=9\cdot\dfrac{44}{45}=\dfrac{44}{5}\)

Gọi số cần tìm có dạng là \(X=\overline{ab}\)
Khi viết thêm chữ số 0 vào giữa hai chữ số thì ta được số mới gấp 6 lần số cũ nên \(\overline{a0b}=6\cdot\overline{ab}\)
=>\(100a+b=6\left(10a+b\right)\)
=>100a+b=60a+6b
=>40a=5b
=>8a=b
=>b=8; a=1
Vậy: Số cần tìm là 18

a; a - b = 6 và \(\overline{4a7}\) + \(\overline{1b5}\) ⋮ 9
Để \(\overline{4a7}\) + \(\overline{1b5}\) ⋮ 9 ⇔ 4 + a + 7 + 1 + b + 5 ⋮ 9
⇒(4 + 7 + 1 + 5) + a + b ⋮ 9
⇒ 17 + a + b ⋮ 9
⇒ 8 + a + b ⋮ 9
Vì a + b ≤ 18 ⇒ 8 + a + b ≤ 26 ⇒ 8 + a + b = 9; 18 (1)
a - b = 6 ⇒ a = 6 + b Thay a = 6 + b vào (1) ta có:
8 + 6 + b + b = 9; 18 ⇒ (8 + 6) + (b + b) = 9; 18
⇒ 14 + 2b = 9; 18
Lập bảng ta có:
| 14 + 2b | 9 | 18 |
| b | -\(\dfrac{5}{2}\) | 2 |
| a = 6 + b | 8 | |
| a; b \(\in\) N; 0 ≤ a; b ≤ 9 | loại |
Theo bẳng trên ta có (a; b) = (8; 2)
b; a - b = 6 và \(\overline{7a5}\) + \(\overline{8b4}\) ⋮ 9
\(\overline{7a5}\) + \(\overline{8b4}\) ⋮ 9 ⇔ 7 + a + 5 + 8 + b + 4 ⋮ 9 ⇒ (7 + 5 + 8 + 4) + a + b⋮ 9
⇒ (12 + 8 + 4) + a + b ⋮ 9 ⇒ (20 + 4) + a + b ⋮ 9 ⇒ 24 + a + b ⋮ 9
⇒ 6 + a + b ⋮ 9 vì 0 ≤ a + b ≤ 18 ⇒ 6 ≤ 6 + a + b ≤ 24
⇒ 6 + a + b = 9; 18 (1)
a - b = 6 ⇒ a = 6 + b thay a = b + 6 vào (1) ta có:
6 + 6 + b + b = 9; 18 ⇒ (6 + 6) + (b + b) = 9; 18 ⇒ 12 +2b = 9; 18
Lập bảng ta có:
| 12 + 2b | 9 | 18 |
| b | - \(\dfrac{3}{2}\) | 3 |
| a = 6 + 3 | 9 | |
| 0 ≤ a; b ≤ 9; a; b \(\in\) N | Loại |
Theo bảng trên ta có:
(a; b) = (9; 3)

a; a - b = 6 và \(\overline{4a7}\) + \(\overline{1b5}\) ⋮ 9
Để \(\overline{4a7}\) + \(\overline{1b5}\) ⋮ 9 ⇔ 4 + a + 7 + 1 + b + 5 ⋮ 9
⇒(4 + 7 + 1 + 5) + a + b ⋮ 9
⇒ 17 + a + b ⋮ 9
⇒ 8 + a + b ⋮ 9
Vì a + b ≤ 18 ⇒ 8 + a + b ≤ 26 ⇒ 8 + a + b = 9; 18 (1)
a - b = 6 ⇒ a = 6 + b Thay a = 6 + b vào (1) ta có:
8 + 6 + b + b = 9; 18 ⇒ (8 + 6) + (b + b) = 9; 18
⇒ 14 + 2b = 9; 18
Lập bảng ta có:
| 14 + 2b | 9 | 18 |
| b | -\(\dfrac{5}{2}\) | 2 |
| a = 6 + b | 8 | |
| a; b \(\in\) N; 0 ≤ a; b ≤ 9 | loại |
Theo bẳng trên ta có (a; b) = (8; 2)
b; a - b = 6 và \(\overline{7a5}\) + \(\overline{8b4}\) ⋮ 9
\(\overline{7a5}\) + \(\overline{8b4}\) ⋮ 9 ⇔ 7 + a + 5 + 8 + b + 4 ⋮ 9 ⇒ (7 + 5 + 8 + 4) + a + b⋮ 9
⇒ (12 + 8 + 4) + a + b ⋮ 9 ⇒ (20 + 4) + a + b ⋮ 9 ⇒ 24 + a + b ⋮ 9
⇒ 6 + a + b ⋮ 9 vì 0 ≤ a + b ≤ 18 ⇒ 6 ≤ 6 + a + b ≤ 24
⇒ 6 + a + b = 9; 18 (1)
a - b = 6 ⇒ a = 6 + b thay a = b + 6 vào (1) ta có:
6 + 6 + b + b = 9; 18 ⇒ (6 + 6) + (b + b) = 9; 18 ⇒ 12 +2b = 9; 18
Lập bảng ta có:
| 12 + 2b | 9 | 18 |
| b | - \(\dfrac{3}{2}\) | 3 |
| a = 6 + 3 | 9 | |
| 0 ≤ a; b ≤ 9; a; b \(\in\) N | Loại |
Theo bảng trên ta có:
(a; b) = (9; 3)

2:
\(AM=\dfrac{1}{3}\cdot AB=\dfrac{1}{3}\cdot48=16\left(cm\right)\)
\(AN=\dfrac{1}{2}\cdot AD=\dfrac{1}{2}\cdot36=18\left(cm\right)\)
ΔAMN vuông tại A
=>\(S_{AMN}=\dfrac{1}{2}\times AM\times AN=\dfrac{1}{2}\times16\times18=144\left(cm^2\right)\)
BM+AM=BA
=>BM+16=48
=>BM=32(cm)
AN+ND=AD
=>ND+18=36
=>ND=18(cm)
ΔNDC vuông tại D
=>\(S_{NDC}=\dfrac{1}{2}\times ND\times DC=\dfrac{1}{2}\times18\times48=432\left(cm^2\right)\)
ΔMBC vuông tại B
=>\(S_{MBC}=\dfrac{1}{2}\times BM\times BC=\dfrac{1}{2}\times32\times36=576\left(cm^2\right)\)
ABCD là hình chữ nhật
=>\(S_{ABCD}=AB\times AD=48\times36=1728\left(cm^2\right)\)
\(S_{ABCD}=S_{AMN}+S_{NDC}+S_{MBC}+S_{MNC}\)
=>\(S_{MNC}+144+432+576=1728\)
=>\(S_{MNC}=576\left(cm^2\right)\)

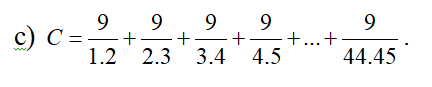


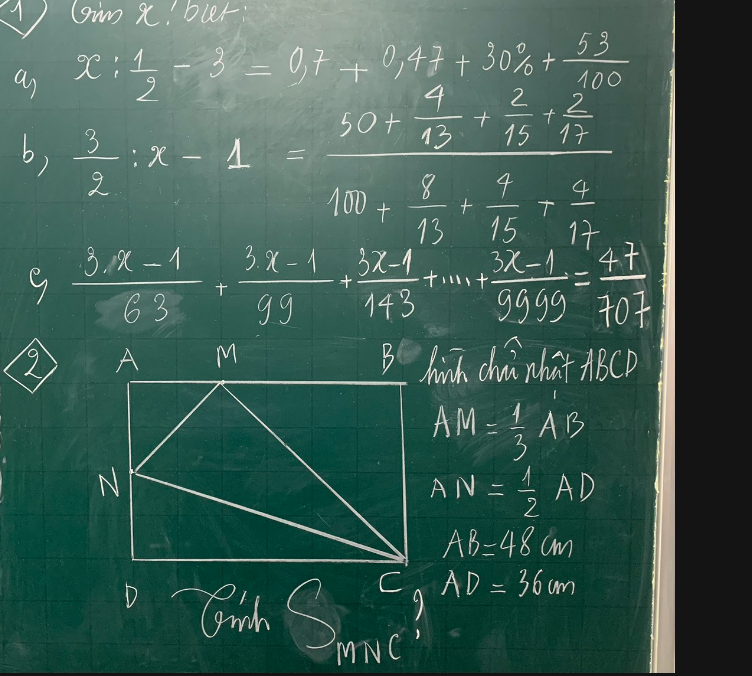
Gọi số học sinh đi tham quan là \(a\)
Điều kiện: \(a\inℕ^∗;700\le a\le1200\)
Ta có:
+) Nếu xếp 30 em hay 45 em vào 1 xe thì đều thiếu 5 em
⇒\(a\) chia \(30\) hay \(45\) thiếu \(5\)
\(\Rightarrow a+5⋮30;45\)
\(\Rightarrow a+5\in BC\left(30;45\right)=\left\{0,90,180,270,360,450,540,630,720,810,900,990,1080,1170,1260,...\right\}\)
Mà \(700\le a\le1200\) nên \(705\le a+5\le1205\) suy ra:
\(a\in\left\{720,810,900,990,1080,1170\right\}\)
+) Nếu xếp 43 em vào một xe thì vừa đủ
\(\Rightarrow a⋮43\)
Do đó: \(a=1075\) (thỏa mãn điều kiện)
Vậy...
Gọi tổng số h/s là A
A:30 thiếu 5 , chia 45 cũng thiếu 5 ≠Ta có :
A+5 ∈ BCNN(45,30)700≤A≤1200
30=2.3.5
45=2.3.3.5=2.32.5
BCNN(30,45)=2.95=90
BC(30,45)={0,90,180,270,360,450,540,630,720,810,900,990,1080,1170} mà 700≤A≤1200 nên loại các số 0,90,180,270,360,450,540,630.
Nếu A là 1 trong các số trên thì phải trừ đi 5 , A ∈={715,805,895,985,1075,1165}
Vì A⋮43 nên A sẽ bằng 1075 , vậy chuyến đi đó có 1075 h/s lớp 6
Đáp số 1075 h/s