Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d: \(CD\subset\left(HKCD\right)\)
\(CD\subset\left(ABCD\right)\)
Do đó: \(\left(HKCD\right)\cap\left(ABCD\right)=CD\)
a: \(O\in BD\subset\left(SBD\right)\)
\(O\in AC\subset\left(SAC\right)\)
Do đó: \(O\in\left(SBD\right)\cap\left(SAC\right)\)
=>\(\left(SBD\right)\cap\left(SAC\right)=SO\)
b: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
c; AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC

a: \(O\in BD\subset\left(SBD\right)\)
\(O\in AC\subset\left(SAC\right)\)
=>\(O\in\left(SBD\right)\cap\left(SAC\right)\)
=>\(\left(SBD\right)\cap\left(SAC\right)=SO\)
b: \(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
=>(SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
c: \(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC
d: \(CD\subset\left(HKCD\right)\)
\(CD\subset\left(ABCD\right)\)
Do đó: (HKCD) giao (ABCD)=CD

a: Trong mp(ABCD), Gọi giao của AC và BD là O
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà S thuộc (SAC) giao (SBD)
nên (SAC) giao (SBD)=SO
b:Trong mp(ABCD), Gọi giao của AB và CD là M
\(M\in AB\subset\left(SAB\right)\)
\(M\in CD\subset\left(SCD\right)\)
=>M thuộc (SAB) giao (SCD)
mà S thuộc (SAB) giao (SCD)
nên (SAB) giao (SCD)=SM
c: Trong mp(ABCD), gọi N là giao của AD với BC
\(N\in AD\subset\left(SAD\right);N\in BC\subset\left(SBC\right)\)
Do đó: \(N\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SN\)

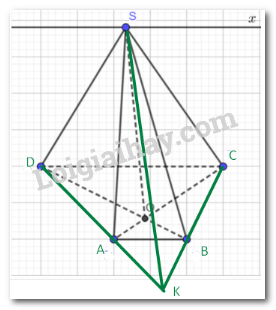
a) Gọi giao điểm của AD và BC là K.
Ta có: SK cùng thuộc mp(SAD) và (SBC).
Vậy SK là giao tuyến của (SAD) và (DBC).
b) (SAB) và (SCD) có AB // CD và S chung nên giao tuyến là dường thẳng Sx đi qua x và song song với AB và CD.
c) Gọi O là giao điểm của AC và BD suy ra O thuộc giao tuyến của (SAC) và (SBC)
Suy ra SO là giao tuyến của (SAC) và (SBD).

a: \(I\in BD\subset\left(SBD\right)\)
\(I\in AC\subset\left(SAC\right)\)
Do đó: \(I\in\left(SBD\right)\cap\left(SAC\right)\)
=>\(\left(SBD\right)\cap\left(SAC\right)=SI\)
b: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
c: AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC

a. \(\left(SAB\right)\cap\left(SBC\right)=?\)
Ta có: \(\left\{{}\begin{matrix}S\in\left(SAB\right),\left(SBC\right)\\B\in\left(SAB\right),\left(SBC\right)\end{matrix}\right.\)\(\Rightarrow\)\(\left(SAB\right)\cap\left(SBC\right)=SB\)
b. \(\left(SAB\right)\cap\left(SCD\right)=?\)
Xét mp (SAB), kẻ Sx//AB
Ta có: Sx//AB, AB//CD \(\Rightarrow\) CD//Sx
Lại có: \(S\in\left(SAB\right),\left(SCD\right)\)
\(\Rightarrow\)\(\left(SAB\right)\cap\left(SCD\right)=Sx\)
c. \(\left(SAD\right)\cap\left(SBC\right)=?\)
Xét mp (ABCD), ta có không song song với BC
Gọi \(I=AD\cap BC\)
Ta có: \(\left\{{}\begin{matrix}S\in\left(SAD\right),\left(SBC\right)\\I\in\left(SAD\right),\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow\)\(\left(SAD\right)\cap\left(SBC\right)=SI\)

a: \(E\in AC\subset\left(SAC\right)\)
\(E\in BD\subset\left(SBD\right)\)
Do đó: \(E\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SE\)
b: Gọi K là giao của AD với BC
\(K\in AD\subset\left(SAD\right)\)
\(K\in BC\subset\left(SBC\right)\)
Do đó: \(K\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(SK=\left(SAD\right)\cap\left(SBC\right)\)
c: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: \(\left(SAB\right)\cap\left(SCD\right)=xy\), xy đi qua S và xy//AB//CD

a: \(E\in AC\subset\left(SAC\right);E\in BD\subset\left(SBD\right)\)
=>\(E\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SE\)
b: Gọi K là giao của AD và BC
\(K\in AD\subset\left(SAD\right);K\in BC\subset\left(SBC\right)\)
=>\(K\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SK\)
c: Xét (SAB) và (SCD) có
AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: (SAB) giao (SCD)=xy; xy đi qua S và xy//AB//CD


Khó dứ dậy giời
Phần 1 — Chứng minh tứ giác \(A E H F\) nội tiếp
Gọi \(D \in B C , \textrm{ }\textrm{ } E \in C A , \textrm{ }\textrm{ } F \in A B\) là các chân đường cao (tức \(A D , B E , C F\) là các đường cao) và \(H\) là trực tâm (giao của 3 đường cao).
Quan sát:
Do đó \(\angle A E H = \angle A F H = 90^{\circ}\). Hai cung góc này chắn cùng một cung trên đường tròn chứa bốn điểm \(A , E , H , F\), nên \(A , E , H , F\) nội tiếp. □
Lưu ý trước khi làm hai câu tiếp theo
Trên ảnh đề viết: “Gọi \(K\) là trung điểm \(B C\). Chứng minh \(H K \bot A O\).”
Ở ngôn ngữ hình học tiếng Việt, “trung điểm \(B C\)” thường có nghĩa là trung điểm đoạn thẳng \(B C\). Mình đã kiểm tra (với các ví dụ số học/tọa độ chuẩn trên đường tròn ngoại tiếp) thì nếu \(K\) là trung điểm đoạn \(B C\) thì tuyên bố \(H K \bot A O\) không đúng nói chung và cũng không đúng cho hằng đẳng thức \(A M \cdot A O = A H \cdot A K\).
Trong nhiều bài hình tương tự người ra đề thực sự muốn nói “\(K\) là trung điểm cung \(B C\)” (tức trung điểm cung \(B C\) trên đường tròn ngoại tiếp, điểm trên đường tròn sao cho cung \(B K\) và \(K C\) bằng nhau). Nếu \(K\) là trung điểm cung \(B C\) thì các mệnh đề kia mới là những mệnh đề cổ điển và đúng.
Vì vậy mình sẽ:
Mình tiếp tục theo phần (A) vì đó là cách bài toán thường gặp.
Phần 2 — Giả sử \(K\) là trung điểm cung \(B C\) của đường tròn \(\left(\right. O \left.\right)\). Chứng minh \(H K \bot A O\).
Lời giải (một cách chuẩn, bằng đối xứng trên đường tròn):
(Đây là một lối lý giải tiêu chuẩn trong các bài hình: phản chiếu trực tâm qua trung điểm cung BC cho antipode của A ⇒ K là trung điểm HM ⇒ kết hợp với O là trung điểm AM dẫn tới kết luận vuông góc.)
Phần 3 — Với \(M\) như trên (giao \(A O\) với \(\left(\right. O \left.\right)\), \(M \neq A\)), chứng minh
\(A M \cdot A O = A H \cdot A K .\)
Lời giải (ý chính):