Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đầu tiên, cứ gọi 2 sợi dây là A và B cho dễ nhé. Muốn giải được câu đố này, bạn phải dựa vào dữ kiện duy nhất được cung cấp: A và B đều cháy hết trong vòng 1 giờ đồng hồ khi đốt cháy một đầu.
Điều này có nghĩa là nếu đốt cháy 2 đầu, sợi dây sẽ cháy trong đúng 30 phút. Và sau khi cháy được một nửa, bạn đốt nốt đầu còn lại, thì khoảng thời gian cho đoạn dây còn lại cháy hết sẽ đúng bằng 15 phút.
Vậy vấn đề bây giờ chỉ là làm cách nào đo được chính xác thời điểm đoạn dây cháy còn một nửa mà thôi.
Dễ quá rồi đúng không: Với dây A, hãy đốt cháy 2 đầu, đồng thời đốt một đầu của dây B.

Đáp án của câu đố kinh điển trên.
Khi dây A cháy hết, dây B sẽ còn 30 phút nữa để cháy. Giờ hãy châm lửa vào đầu còn lại của dây B, và khi B cháy hết, chính xác 45 phút đã trôi qua.
nha hoc24

Tỉ lệ vận tốc của xe máy lúc đi và lúc về là:
\(25:30=\frac{5}{6}\)
=> Tỉ lệ thời gian của xe máy lúc đi và lúc về là \(\frac{6}{5}\)
Đổi: \(20p=\frac{1}{3}h\)
Thời gian xe máy lúc đi là:
\(\frac{1}{3}.6=2\) (giờ)
Quãng đường AB dài:
\(25.2=50\) (km)
Đáp số: 50 km
Mình giải đc đó ![]()


a) Tính chiều cao trung bình của học sinh nam
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp :
\(\overline{x}=\dfrac{1}{60}\left(5.140+9.150+19.160+17.170+10.180\right)\)
\(\overline{x}=163\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(8,33.140+15.150+31,67.160+28,33.170+16,67.180\right)\)\(\overline{x}=163\)
Tính chiều cao trung bình của học sinh nữ:
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp \(\overline{x}=\dfrac{1}{60}\left(8.140+15.150+16.160+14.170+7.180\right)\)
\(\overline{x}=159,5\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(13,33.140+25.150+26,67.160+23,33.170+11,67.180\right)\)
\(\overline{x}=159,5\)
b) Vì \(\overline{x}_{nam}=163>\overline{x}_{nữ}=159,5\) nên suy ra học sinh ở nhóm nam cao hơn học sinh ở nhóm nữ
c) \(\overline{x}=\left(60.159,5+60.163\right)\dfrac{1}{2}\approx161\left(cm\right)\)

Lời giải:
GTLN:
Áp dụng BĐT Cauchy-Schwarz:
\(B^2=(6\sqrt{x-1}+8\sqrt{3-x})^2\leq (6^2+8^2)(x-1+3-x)=200\)
\(\Rightarrow B_{\max}= 10\sqrt{2}\Leftrightarrow \frac{3}{\sqrt{x-1}}=\frac{4}{\sqrt{3-x}}\Leftrightarrow x=\frac{43}{25}\)
GTNN:
Ta biết một bổ đề sau: Với \(a,b\geq 0\Rightarrow \sqrt{a}+\sqrt{b}\geq \sqrt{a+b}\)
Cách CM rất đơn giản vì nó tương đương với \(\sqrt{ab}\geq 0\) (luôn đúng)
Áp dụng vào bài toán:
\(\Rightarrow B\geq \sqrt{36x-36+192-64x}=\sqrt{156-28x}\geq 6\sqrt{2}\) (do \(x\leq 3\))
Vậy \(B_{\min}=6\sqrt{2}\Leftrightarrow x=3\)

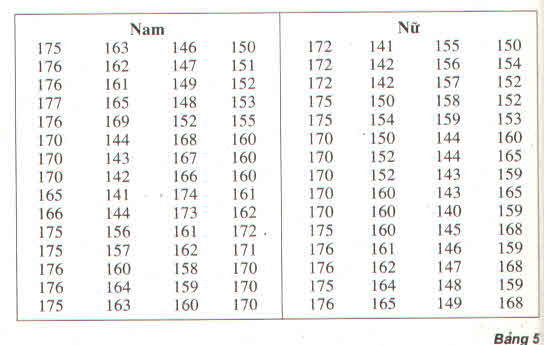
a) Dãy các số liệu chiều cao của các học sinh nam ở bảng 5 có :
\(\overline{x_1}\approx163\left(cm\right);s_1^2\approx134,3;s_1\approx11,59\)
Dãy các số liệu chiều cao của các học sinh nữ cho ở bảng 5 có :
\(\overline{x_2}\approx159,5\left(cm\right);s_2^2\approx148;s_2\approx12,17\)
b) Nhóm T có \(\overline{x_3}=163\left(cm\right);s_3^2=169;s_3=13\)
Học sinh ở nhóm nam và nhóm T có chiều cao như nhau và cùng lớn hơn chiều cao của học sinh ở nhóm nữ (vì \(\overline{x}_1=\overline{x}_3>\overline{x}_2\)
Vì \(\overline{x}_1=\overline{x}_3=163\left(cm\right)\) và \(s_1< s_3\) nên chiều cao của các học sinh nam đồng đều hơn chiều cao của các học sinh nhóm T
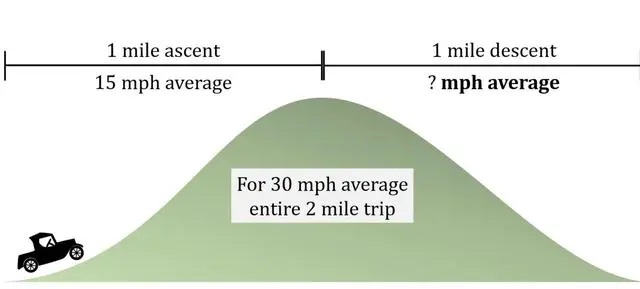







Không có vận tốc thực tế nào có thể đạt được yêu cầu này.
Chiếc xe phải xuống dốc với vận tốc vô hạn, điều đó là bất khả thi.
tham khảo