Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1)
a) Vì A: B:C:D = 1:2:3:4
=> A= B/2 = C/3=D/4
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
A = 36 độ
B= 72 độ
C=108 độ
D= 144 độ
b) Ta có :
A + D = 36 + 144 = 180 độ(1)
B+C = 72 + 108 = 180 độ(2)
Từ (1) và (2) ta có:
=> AB //CD (dpcm)
c) Ta có :
CDE + ADC = 180 độ(kề bù)
=> CDE = 180 - 144 = 36
Ta có :
BCD + DCE = 180 độ ( kề bù)
=> DCE = 180 - 108 = 72
Xét ∆CDE ta có :
CDE + DCE + DEC = 180 ( tổng 3 góc trong ∆)
=> DEC = 180 - 72 - 36 = 72 độ
Bài 2)
a) Ta có ABCD có :
A + B + C + D = 360 độ
Mà C = 80 độ
D= 70 độ
=> A+ B = 360 - 80 - 70 = 210 độ
Ta có AI là pg góc A
BI là pg góc B
=> DAI = BAI = A/2
=> ABI = CBI = B/2
=> BAI + ABI = A + B /2
=> BAI + ABI = 210/2 = 105
Xét ∆IAB ta có :
IAB + ABI + AIB = 180 độ
=> AIB = 180 - 105
=> AIB = 75 độ
=>

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
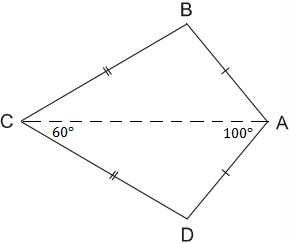
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000

a) ta thấy ab = ab ; bc = cd
=> tứ giác ABCD là hình bình hành
=> AC và BD cắt nhau tai trung điểm của mỗi đường
=> AC là đường trung trực của BD
b) Ta có A + D = 180
=> D = 180 - 100
=> D= 80
Ta lại có B + C = 180
=> C = 180 - 60
=> C = 120

Từ \(A B = B C\) ⇒ Tam giác \(A B C\) cân tại \(B\)
Từ \(C D = D A\) ⇒ Tam giác \(C D A\) cân tại \(D\)
Gọi \(B D\) cắt \(A C\) tại \(O\)
Cần chứng minh:
- \(O\) là trung điểm của \(A C\)
- \(B D \bot A C\)
- Xét hai tam giác \(A B C\) và \(C D A\):
- Từ \(A B = B C\) ⇒ \(\angle B A C = \angle B C A\)
- Từ \(C D = D A\) ⇒ \(\angle D C A = \angle D A C\)
Nếu 2 tam giác \(A B C\) và \(C D A\) xếp đối xứng nhau qua đường chéo \(B D\), thì các cặp đỉnh tương ứng đối xứng qua \(B D\), nghĩa là:
- \(A\) và \(C\) đối xứng nhau qua \(B D\)
- Do đó, \(B D\) là trung trực của đoạn \(A C\)
- Tổng 4 góc trong tứ giác:
\(\angle A + \angle B + \angle C + \angle D = 360^{\circ} \Rightarrow \angle A + \angle C = 360^{\circ} - \left(\right. 100^{\circ} + 80^{\circ} \left.\right) = 180^{\circ}\)
Mặt khác:
- Tam giác \(A B C\) cân tại \(B\) ⇒ \(\angle A = \angle C\)
- Hoặc tam giác \(C D A\) cân tại \(D\) ⇒ \(\angle A = \angle C\)
⇒ \(\angle A = \angle C\)
⇒ \(\angle A + \angle C = 180^{\circ} \Rightarrow 2 \angle A = 180^{\circ} \Rightarrow \angle A = \angle C = \boxed{90^{\circ}}\)

a) HS tự chứng minh
b) Sử dụng tổng bốn góc trong tứ giác và chú ý B ^ = D ^

Bài 1:
a: Ta có: AB=AD
nên A nằm trên đường trung trực của BD(1)
Ta có: CB=CD
nên C nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
b: Xét ΔBAC và ΔDAC có
AB=AD
AC chung
BC=DC
Do đó: ΔBAC=ΔDAC
Suy ra: \(\widehat{B}=\widehat{D}\)
=>\(\widehat{B}=\widehat{D}=\dfrac{200^0}{2}=100^0\)

Giả thiết
Cho tứ giác cánh diều ABCDABCD với:
Điều này đúng với định nghĩa hình cánh diều: có hai cặp cạnh kề bằng nhau.
🧠 Câu a) Chứng minh AC là đường trung trực của BD
🔷 Phân tích
Gọi OO là giao điểm hai đường chéo ACAC và BDBD. Vì AB=ADAB = AD và CB=CDCB = CD, ta có:
→ Trong tứ giác cánh diều, hai đường chéo vuông góc và đường nối hai đỉnh có cặp cạnh bằng nhau (ở đây là ACAC) sẽ là trục đối xứng.
🧩 Chứng minh
⏬ Vì nó chia BDBD thành hai phần bằng nhau và vuông góc tại điểm OO
✅ Kết luận: AC là đường trung trực của BD
📐 Câu b) Tính số đo góc BB và góc DD, biết:
🧮 Sử dụng tổng góc tứ giác
Trong mọi tứ giác:
∠A+∠B+∠C+∠D=360∘\angle A + \angle B + \angle C + \angle D = 360^\circThay số:
100∘+∠B+70∘+∠D=360∘⇒∠B+∠D=190∘100^\circ + \angle B + 70^\circ + \angle D = 360^\circ \Rightarrow \angle B + \angle D = 190^\circ📏 Tính thêm
Vì hình cánh diều có trục đối xứng là đường chéo ACAC, hai góc ở hai đầu đường chéo BDBD là góc BB và góc DD, nên:
Khi đó:
∠B+∠D=2∠B=190∘⇒∠B=∠D=95∘\angle B + \angle D = 2\angle B = 190^\circ \Rightarrow \angle B = \angle D = 95^\circ✅ Kết quả:
a: Ta có: AB=AD
=>A nằm trên đường trung trực của BD(1)
Ta có: CB=CD
=>C nằm trên đường trung trực của BD(2)
từ (1),(2) suy ra AC là đường trung trực của BD
b: Xét tứ giác ABCD có \(\hat{ABC}+\hat{ADC}+\hat{BAD}+\hat{BCD}=360^0\)
=>\(\hat{ABC}+\hat{ADC}=360^0-100^0-70^0=190^0\)
Xét ΔABC và ΔADC có
AB=AD
BC=DC
AC chung
Do đó: ΔABC=ΔADC
=>\(\hat{ABC}=\hat{ADC}=\frac{190^0}{2}=95^0\)