K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

8 tháng 9 2023
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.

CM
6 tháng 4 2018
Ta ghép như sau:
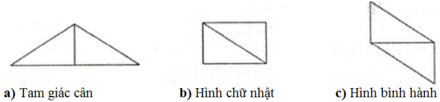
Diện tích 3 hình này đều bằng nhau vì cùng bằng tổng diện tích của hai tam giác vuông ban đầu.

21 tháng 4 2017
Cắt hai tam giác vuông bằng nhau từ một tấm bìa, chẳng hạn ta được hai hình sau:
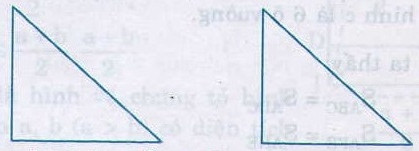
Ghép hai tam giác trên để tạo thành:
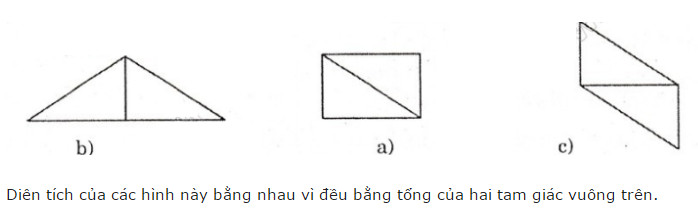
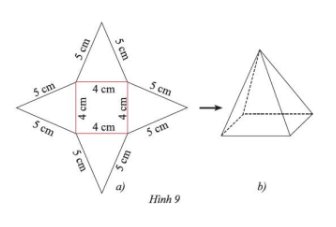
Cạnh đáy sẽ là \(12 - 2 x\) (vì cắt x hai bên chiều dài và rộng)
Là x (chính là cạnh hình vuông cắt ra và gấp lên)
\(V = x \times \left(\right. 12 - 2 x \left.\right) \times \left(\right. 12 - 2 x \left.\right) = x \left(\right. 12 - 2 x \left.\right)^{2}\)
Ta sẽ tìm cực trị hàm số:
\(V \left(\right. x \left.\right) = x \left(\right. 12 - 2 x \left.\right)^{2}\)
\(V \left(\right. x \left.\right) = x \left(\right. 144 - 48 x + 4 x^{2} \left.\right) = 144 x - 48 x^{2} + 4 x^{3}\)
\(V^{'} \left(\right. x \left.\right) = 144 - 96 x + 12 x^{2}\)
\(V^{'} \left(\right. x \left.\right) = 0\):
\(144 - 96 x + 12 x^{2} = 0\)
Chia cả phương trình cho 12:
\(12 - 8 x + x^{2} = 0\)
Hay:
\(x^{2} - 8 x + 12 = 0\)
\(x = \frac{8 \pm \sqrt{64 - 48}}{2} = \frac{8 \pm \sqrt{16}}{2} = \frac{8 \pm 4}{2}\)
Hai nghiệm:
thể tích lớn nhất:
\(V = 2 \times 8^{2} = 2 \times 64 = 128 \&\text{nbsp};\text{cm}^{3}\)
vậy