K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
1
A
22 tháng 6 2021
Ps : Bn tự vẽ hình nhé, mk chỉ giải thôi ạ.
a) Xét \(\Delta ABC\)và \(\Delta HAB\)
\(\widehat{BAC}=\widehat{BHA}=90^O\)
\(\widehat{ABC}chung\)
\(\Rightarrow\Delta ABC~\Delta HBA\)( g - g )
b) Xét \(\Delta AHD\)và \(\Delta CED\)
\(\widehat{AHD}=\widehat{CED}=90^O\)
\(\widehat{ADH}=\widehat{CDE}\)( đối đỉnh )
\(\Rightarrow\Delta AHD~\Delta CED\left(g-g\right)\)
\(\Rightarrow\frac{AH}{AD}=\frac{CE}{CD}\Rightarrow AH.CD=AD.CE\)
c) Vì H là trung điểm của BD mà \(AH\perp BD\)
=> AH là đường trung trực của BD
\(\Rightarrow AB=AD\)
Mà : \(\frac{AH}{AD}=\frac{CE}{CD}\)
\(\Rightarrow\frac{AH}{AB}=\frac{CE}{CD}\)
Vì \(\Delta ABC~\Delta HBA\Rightarrow\frac{AH}{AB}=\frac{CA}{CB}\)
Do đó : \(\frac{CE}{CD}=\frac{CA}{CB}=\frac{8}{10}=\frac{4}{5}\)
Vì \(\Delta CED\)vuông
\(\Rightarrow S_{CED}=\frac{CE.ED}{2}\)
\(AB//FK\Rightarrow\widehat{BAH}=\widehat{KFH}\)
\(\widehat{AHB}=\widehat{FHK}=90^O\)
\(BA=HD\)
\(\Rightarrow\Delta AHB=\Delta FHK\)
\(\Rightarrow HA=HF\)mà \(CH\perp AF\)
=> CH là đường trung trực AF \(\Rightarrow\Delta ACF\)cân tại C
Do đó : D là trọng tâm \(\Delta ACF\)
\(\Rightarrow CD=\frac{2}{3}CH\)
Mà \(\cos ACB=\frac{AC}{BC}=\frac{CH}{CA}=\frac{4}{5}\Rightarrow CH=\frac{32}{5}\Rightarrow CD=\frac{64}{15}\)
\(\Rightarrow\frac{CE}{CD}=\frac{4}{5}\Rightarrow CE=\frac{256}{75}\)
\(ED=\sqrt{CD^2-CE^2}=\frac{64}{25}\)
\(\Rightarrow S_{CED}=\frac{8192}{1875}\)
d) Vì \(\Delta ACF\)cân tại C \(\Rightarrow KE//AF\Rightarrow\widehat{EKF}=\widehat{AFK}\)
Vì HK là trung tuyến \(\Delta AFK\)\(\Rightarrow\widehat{AFK}=\widehat{HKF}\)
Do đó : \(\widehat{HKF}=\widehat{EKF}\)
=> KD là phân giác \(\widehat{HKE}\)
# Aeri #
NQ
1
23 tháng 8
a: ta có: EI⊥BF
AC⊥BF
Do đó: EI//AC
=>\(\hat{IEB}=\hat{ACB}\) (hai góc đồng vị)
mà \(\hat{ABC}=\hat{ACB}\) (ΔABC cân tại A)
nên \(\hat{KBE}=\hat{IEB}\)
Xét ΔKBE vuông tại K và ΔIEB vuông tại I có
BE chung
\(\hat{KBE}=\hat{IEB}\)
Do đó: ΔKBE=ΔIEB
=>EK=BI
b: Điểm D ở đâu vậy bạn?
11 tháng 8
1: \(\frac{1-a\cdot\sqrt{a}}{1-\sqrt{a}}=\frac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)^{}}{1-\sqrt{a}}=1+\sqrt{a}+a\)
2: \(\frac{\sqrt{x+3}+\sqrt{x-3}}{\sqrt{x+3}-\sqrt{x-3}}=\frac{\left(\sqrt{x+3}+\sqrt{x-3}\right)\left(\sqrt{x+3}+\sqrt{x-3}\right)}{\left(\sqrt{x+3}-\sqrt{x-3}\right)\left(\sqrt{x+3}+\sqrt{x-3}\right)}\)
\(=\frac{\left(\sqrt{x+3}+\sqrt{x-3}\right)^2}{x+3-\left(x-3\right)}=\frac{x+3+x-3+2\sqrt{\left(x+3\right)\left(x-3\right)}}{6}\)
\(=\frac{2x+2\sqrt{x^2-9}}{6}=\frac{x+\sqrt{x^2-9}}{3}\)
4: \(\frac{3}{2\sqrt{9x}}=\frac{3}{2\cdot3\sqrt{x}}=\frac{1}{2\sqrt{x}}=\frac{\sqrt{x}}{2}\)
5: \(\frac{1}{2\sqrt{x}}=\frac{1\cdot\sqrt{x}}{2\sqrt{x}\cdot\sqrt{x}}=\frac{\sqrt{x}}{2x}\)
7: \(\frac{\sqrt{a^3}+a}{\sqrt{a}-1}=\frac{a\cdot\sqrt{a}+a}{\sqrt{a}-1}=\frac{a\left(\sqrt{a}+1\right)}{\sqrt{a}-1}=\frac{a\left(\sqrt{a}+1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\frac{a\left(a+2\sqrt{a}+1\right)}{a-1}=\frac{a^2+2a\cdot\sqrt{a}+a}{a-1}\)
8: \(\frac{2}{\sqrt{a}+\sqrt{2b}}=\frac{2\cdot\left(\sqrt{a}-\sqrt{2b}\right)}{\left(\sqrt{a}+\sqrt{2b}\right)\left(\sqrt{a}-\sqrt{2b}\right)}=\frac{2\sqrt{a}-2\sqrt{2b}}{a-2b}\)
10: \(\frac{25}{\sqrt{a}-\sqrt{b}}=\frac{25\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{25\sqrt{a}+25\sqrt{b}}{a-b}\)
11: \(-\frac{ab}{\sqrt{a}-\sqrt{b}}=-\frac{ab\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{-ab\cdot\sqrt{a}-ab\cdot\sqrt{b}}{a-b}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2024
a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)
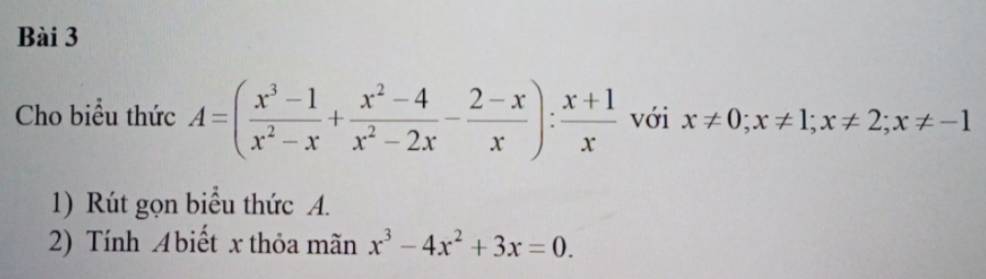
Xét tam giác vuông có chéo \(A C\) và \(B D\) vuông góc nhau. Ta sử dụng một kết quả hình học cổ điển:
Chứng minh bằng tọa độ (nếu cần formal hơn):
Giả sử đặt hệ trục tọa độ như sau:
Khi đó:
Đường chéo \(A C = \overset{⃗}{A C} = \left(\right. c , h \left.\right)\)
Đường chéo \(B D = \overset{⃗}{B D} = \left(\right. - b , h \left.\right)\)
Hai đường chéo vuông góc → tích vô hướng bằng 0:
\(\overset{⃗}{A C} \cdot \overset{⃗}{B D} = c \cdot \left(\right. - b \left.\right) + h \cdot h = - b c + h^{2} = 0 \Rightarrow h^{2} = b c\)
Ta chứng minh:
\(h = \frac{A B + C D}{2} = \frac{b + c}{2} \Rightarrow h^{2} = \left(\left(\right. \frac{b + c}{2} \left.\right)\right)^{2} = \frac{b^{2} + 2 b c + c^{2}}{4}\)
So sánh với \(h^{2} = b c\), ta cần:
\(\frac{b^{2} + 2 b c + c^{2}}{4} = b c \Rightarrow b^{2} + 2 b c + c^{2} = 4 b c \Rightarrow b^{2} - 2 b c + c^{2} = 0 \Rightarrow \left(\right. b - c \left.\right)^{2} = 0 \Rightarrow b = c\)
=> Hai đáy bằng nhau ⇒ hình thang trở thành hình thang cân, và trong trường hợp đặc biệt này, kết quả vẫn đúng.
✅ Kết luận:
Với giả thiết: hai đường chéo vuông góc, ta chứng minh được:
\(A H = \frac{A B + C D}{2}\)