Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(255=5\cdot51=5\cdot3\cdot17\)
b: \(630=63\cdot10=3^2\cdot7\cdot2\cdot5\)

5871 : [ 928 – (247 – 82 x 5)]
= 5871 : [928 – (247 – 410)]
= 5871 : [928 – (-163)]
= 5871 : 1091
= 5871/1901
phân tích kết quả ra thừa số nguyên tố nữa nhé bạn giúp mình với

\(B=\frac{4^6.9^5+6^9.120}{8^4.3^{12}-6^{11}}=\frac{\left(2^2\right)^6.\left(3^2\right)^5+\left(2.3\right)^9.2^3.3.5}{\left(2^3\right)^4.3^{12}-\left(2.3\right)^{11}}=\frac{2^{12}.3^{10}+2^9.2^3.3^9.3.5}{2^{12}.3^{12}-2^{11}.3^{11}}=\frac{2^{12}.3^{10}+2^{12}.3^{10}.5}{2^{11}.3^{11}.\left(2.3-1\right)}=\frac{2^{12}.3^{10}.\left(1+5\right)}{2^{11}.3^{11}.5}\)
=\(\frac{2^{12}.3^{10}.6}{2^{11}.3^{11}.5}=\frac{2^{13}.3^{11}}{2^{11}.3^{11}.5}=\frac{2^2}{5}=\frac{4}{5}\)


Ta có công thức: \(ab=\left(a,b\right).\left[a,b\right]\).
Áp dụng ta được:
Có \(120.200=24000\), \(BCNN\left(120,200\right)=600\)
suy ra \(ƯCLN\left(120,200\right)=\frac{24000}{600}=40\).

\(a=p_1^m.p_2^n\Rightarrow a^3=p_1^{3m}.p_2^{3m}.\) Số ước của \(a^3\)là ( 3m + 1 ) ( 3n + 1 ) = 40 , suy ra m = 1 , n = 3 ( hoặc m = 3 , n = 1 )
Số \(a^2=p_1^{2m}.p_2^{2n}\) có số ước là ( 2m + 1 ) ( 2n + 1 ) = 3 . 7 = 21 ( ước )
ủng hộ mk nhé k nhiều vô .
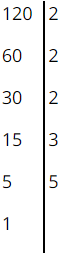
310 = 2 x 5 x 31
\(2020=2^2\times5\times101\)