Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B A C H I S
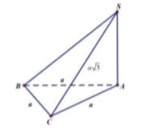
Gọi H là trung điểm của BC, suy ra \(SH\perp BC\). Mà (SBC) vuông góc với (ABC) theo giao tuyến BC, nên \(SH\perp\left(ABC\right)\)
Ta có : \(BC=a\Rightarrow SH=\frac{a\sqrt{3}}{2}\); \(AC=BC\sin30^0=\frac{a}{2}\)
\(AB=BC.\cos30^0=\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABC}=\frac{1}{6}SH.AB.AC=\frac{a^3}{16}\)
Tam giác ABC vuông tại A và H là trung điểm của BC nên \(HA=HB\). Mà \(SH\perp\left(ABC\right)\), suy ra \(SA=SB=a\). Gọi I là trung điểm của AB, suy ra \(SI\perp AB\)
Do đó \(SI=\sqrt{SB^2-\frac{AB^2}{4}}=\frac{a\sqrt{13}}{4}\)
Suy ra \(d\left(C;\left(SAB\right)\right)=\frac{3V_{S.ABC}}{S_{SAB}}=\frac{6V_{S.ABC}}{SI.AB}=\frac{a\sqrt{39}}{13}\)

Chọn A.
Ta có:
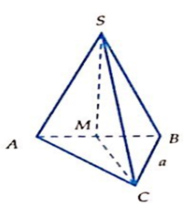
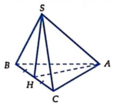
( S A B ) ⊥ ( A B C ) ( S A C ) ⊥ ( A B C ) ( S A B ) ∩ ( S A C ) = S A ⇒ S A ⊥ ( A B C )
S A B C = a 2 3 4 , S A = a 2
Vậy thể tích khối chóp V A B C = a 3 6 12


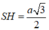 và
và 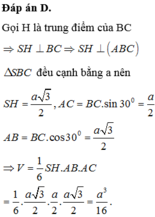

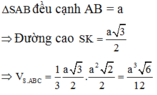

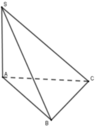
Kẻ H là trung điểm của AB
ΔSAB đều
mà SH là đường trung tuyến
nên SH⊥AB tại H
Ta có: (SAB)\(\cap\) (ABC)=AB
SH⊂(SAB); AB⊂(ABC)
SH⊥AB
Do đó: SH⊥(ABC)
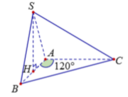
ΔABC đều
=>AB=AC=BC=a
ΔSAB đều
mà SH là đường cao
nên \(SH=a\cdot\frac{\sqrt3}{2}\)
Vì đáy ABC là tam giác đều nên Diện tích đáy là:
\(S_{đáy}=\frac{a^2\sqrt3}{4}\)
Thể tích là:
\(V=\frac13\cdot SH\cdot S_{ABC}=\frac13\cdot\frac{a\sqrt3}{2}\cdot\frac{a^2\sqrt3}{4}=\frac{a^3}{8}\)
Ta cùng giải bài toán một cách đầy đủ, rõ ràng theo hướng hình học lớp 12 nhé.
✅ Đề bài:
Cho hình chóp \(S . A B C\), biết:
Yêu cầu: Tính thể tích khối chóp \(S . A B C\)
🔍 Phân tích bài toán:
Từ giả thiết:
👉 Điều này xác định hình dạng khối chóp hoàn toàn — ta có thể gắn hệ trục tọa độ để tính chính xác các vị trí.
⚙️ Bước 1: Gắn hệ trục tọa độ
Giả sử:
⚙️ Bước 2: Tìm tọa độ điểm \(S\)
Gọi \(S \left(\right. x , y , z \left.\right)\). Ta sẽ tìm sao cho:
Giải nhanh bằng hình học không gian:
👉 Trung điểm AB là:
\(M = \left(\right. \frac{a}{2} , \&\text{nbsp}; 0 , \&\text{nbsp}; 0 \left.\right)\)
\(S = \left(\right. \frac{a}{2} , \&\text{nbsp}; 0 , \&\text{nbsp}; h \left.\right)\)
Tính \(S A = a\):
\(S A = \sqrt{\left(\left(\right. \frac{a}{2} - 0 \left.\right)\right)^{2} + 0^{2} + h^{2}} = a \Rightarrow \left(\left(\right. \frac{a}{2} \left.\right)\right)^{2} + h^{2} = a^{2} \Rightarrow \frac{a^{2}}{4} + h^{2} = a^{2} \Rightarrow h^{2} = \frac{3 a^{2}}{4} \Rightarrow h = \frac{a \sqrt{3}}{2}\)
Vậy:
\(S = \left(\right. \frac{a}{2} , \&\text{nbsp}; 0 , \&\text{nbsp}; \frac{a \sqrt{3}}{2} \left.\right)\)
⚙️ Bước 3: Tính thể tích hình chóp \(S . A B C\)
Công thức:
\(V = \frac{1}{3} \cdot \text{Di}ệ\text{n}\&\text{nbsp};\text{t} \overset{ˊ}{\imath} \text{ch}\&\text{nbsp};đ \overset{ˊ}{\text{a}} \text{y} \cdot \text{Chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{cao}\)
\(S_{đ \overset{ˊ}{\text{a}} \text{y}} = \frac{a^{2} \sqrt{3}}{4}\)
✅ Tính thể tích:
\(V = \frac{1}{3} \cdot \frac{a^{2} \sqrt{3}}{4} \cdot \frac{a \sqrt{3}}{2} = \frac{1}{3} \cdot \frac{a^{3} \cdot 3}{8} = \frac{a^{3}}{8}\)
🎯 Đáp án cuối cùng:
\(\boxed{\frac{a^{3}}{8}}\)
Nếu bạn cần vẽ hình minh họa hoặc lời giải chi tiết hơn theo cách lớp 10-11, mình có thể giúp thêm nhé!