Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện tích xung quanh của hình chóp tam giác đều là: \(\frac{{10.3}}{2}.12 = 180\) (\(c{m^2}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là: \(\frac{{72.4}}{2}.77 = 11088\) (\(d{m^2}\))
Diện tích đáy của hình chóp tứ giác đều là: \({72^2}=5184\) (\(d{m^2}\))
Diện tích toàn phần của hình chóp tứ giác đều là: \(11088 + 5184 = 16 272\) (\(d{m^2}\))
Thể tích của hình chóp tứ giác đều là: \(\frac{1}{3}.5184.68,1=117676,8\) (\(d{m^3}\))

Do mặt bên của hình chóp là tam giác đều cạnh 4cm nên đáy là hình vuông cạnh 4cm
Nửa chu vi đáy là
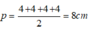
Các mặt bên là tam giác đều cạnh 4cm nên độ dài trung đoạn là
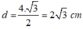

Chọn đáp án A

gọi O là giao điểm của AC và BD => SO vuông góc (ABCD)=>SO vuông góc AO
xét tam giác SAO có SO vuông góc AO
=>SO\(^2\)=SA\(^2\)-AO\(^2\)
=> SO=2\(\sqrt{94}\)
thể tích chóp \(\dfrac{1}{3}\).SO.s.ABCD=\(\dfrac{800}{3}\)\(\sqrt{94}\)

a) Diện tích xung quanh của hình chóp tam giác đều là:
\(\frac{{99.40}}{2}.3 = 5940\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(\frac{{40.34,6}}{2} = 692\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(5940 + 692 = 6632\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.692.98,3 \approx 22674,53\) (\(c{m^3}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là:
\(\frac{{91.120}}{2}.4 = 21840\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(120.120 = 14400\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(21840 + 14400 = 36240\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.14400.68,4 = 328320\) (\(c{m^3}\))

| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | Hình vuông | Ngũ giác đều | Lục giác đều |
| Mặt bên | Tam giác cân | Tam giác cân | Tam giác cân | Tam giác cân |
| Số cạnh đáy | 3 | 4 | 5 | 6 |
| Số cạnh | 6 | 8 | 10 | 12 |
| Số mặt | 4 | 5 | 6 | 7 |

a: SA=SB=SC=5
Gọi H là trung điểm của BC
=>SH là trung đoạn
SH^2=(SB^2+SC^2)/2-BC^2/4=(5^2+5^2)/2-6^2/4=16
=>SH=4cm
b: S SBC=1/2*SH*BC=1/2*4*6=12cm2
=>S xq=3*12=36cm2
Stp=36+6^2*căn 3/4=36+9*căn 3(cm2)
OH=1/3AH=1/3*6*căn 3/2=căn 3(cm)
SO=căn SH^2-OH^2=căn 13(cm)
V=1/3*SO*S ABC=1/3*căn 13*6^2*căn 3/4=3căn 39(cm3)

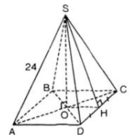
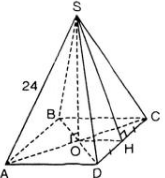
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
⇒ SO2 = SA2 – OA2 = SA2 – (AC/2)2 = 242 - 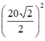 = 376
= 376
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp:
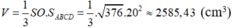
b) Gọi H là trung điểm của CD
SH2 = SD2 – DH2 = 242 – 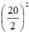 = 476
= 476
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxq = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).


Cho hình chóp tam giác đều có các mặt bên đều là tam giác đều cạnh 20 cm. Ta cần tính thể tích của hình chóp này.
Bước 1: Xác định các yếu tố
- Cạnh tam giác đều đáy: \(a = 20\) cm (vì các mặt bên đều là tam giác đều cạnh 20 cm, đáy cũng là tam giác đều cạnh 20 cm).
- Diện tích đáy \(S_{đ \overset{ˊ}{\text{a}} \text{y}}\) là diện tích tam giác đều cạnh \(a\):
\(S_{đ \overset{ˊ}{\text{a}} \text{y}} = \frac{\sqrt{3}}{4} a^{2} = \frac{\sqrt{3}}{4} \times 20^{2} = \frac{\sqrt{3}}{4} \times 400 = 100 \sqrt{3} \&\text{nbsp};\text{cm}^{2}\)Bước 2: Tính chiều cao của hình chóp \(h\)
Chiều cao \(h\) là khoảng cách từ đỉnh chóp đến mặt phẳng đáy.
Trong hình chóp tam giác đều, đỉnh chóp nằm thẳng trên tâm của tam giác đều đáy.
- Tâm tam giác đều đáy là giao điểm các đường trung tuyến.
- Đường trung tuyến của tam giác đều có độ dài:
\(m = \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{2} \times 20 = 10 \sqrt{3} \&\text{nbsp};\text{cm}\)Mặt bên là tam giác đều cạnh 20 cm, nên độ dài cạnh bên (từ đỉnh chóp đến đỉnh đáy) bằng 20 cm.
Gọi \(h\) là chiều cao hình chóp, \(R\) là khoảng cách từ tâm đáy đến một đỉnh đáy (bán kính đường tròn ngoại tiếp đáy).
- Bán kính đường tròn ngoại tiếp tam giác đều cạnh \(a\) là:
\(R = \frac{a}{\sqrt{3}} = \frac{20}{\sqrt{3}} = \frac{20 \sqrt{3}}{3} \&\text{nbsp};\text{cm}\)Áp dụng định lý Pythagoras trong tam giác vuông tạo bởi chiều cao \(h\), bán kính \(R\), và cạnh bên 20 cm:
\(h = \sqrt{20^{2} - R^{2}} = \sqrt{400 - \left(\left(\right. \frac{20 \sqrt{3}}{3} \left.\right)\right)^{2}} = \sqrt{400 - \frac{400 \times 3}{9}} = \sqrt{400 - \frac{1200}{9}} = \sqrt{400 - 133. \overset{\overline}{3}} = \sqrt{266. \overset{\overline}{6}} \approx 16.33 \&\text{nbsp};\text{cm}\)Bước 3: Tính thể tích hình chóp
Công thức thể tích hình chóp tam giác đều:
\(V = \frac{1}{3} \times S_{đ \overset{ˊ}{\text{a}} \text{y}} \times h = \frac{1}{3} \times 100 \sqrt{3} \times 16.33 = \frac{100 \times 16.33}{3} \sqrt{3} \approx 544.33 \sqrt{3} \&\text{nbsp};\text{cm}^{3}\)Tính gần đúng:
\(\sqrt{3} \approx 1.732 \Rightarrow V \approx 544.33 \times 1.732 \approx 942.7 \&\text{nbsp};\text{cm}^{3}\)Kết luận:
Thể tích hình chóp tam giác đều có các mặt bên là tam giác đều cạnh 20 cm xấp xỉ 942,7 cm³.
Nếu cần, mình có thể giúp bạn giải thích chi tiết hơn hoặc vẽ hình minh họa!
Để tính thể tích hình chóp tam giác đều, bạn cần xác định một số thông số cơ bản, bao gồm diện tích đáy và chiều cao của hình chóp. Ta sẽ thực hiện các bước sau:
Dữ liệu cho bài toán:
Các bước giải quyết:
Bước 1: Tính diện tích đáy của hình chóp
Đáy của hình chóp là một tam giác đều có cạnh 20 cm. Diện tích của tam giác đều được tính bằng công thức:
\(A_{đ \overset{ˊ}{\text{a}} \text{y}} = \frac{\sqrt{3}}{4} \times a^{2}\)Trong đó:
Áp dụng vào công thức:
\(A_{đ \overset{ˊ}{\text{a}} \text{y}} = \frac{\sqrt{3}}{4} \times 20^{2} = \frac{\sqrt{3}}{4} \times 400 = 100 \sqrt{3} \approx 173 , 21 \textrm{ } \text{cm}^{2}\)Bước 2: Tính chiều cao của hình chóp
Chiều cao của hình chóp là đoạn thẳng từ đỉnh đến tâm của đáy. Để tính chiều cao này, ta sử dụng hình chiếu vuông góc từ đỉnh xuống đáy.
- Đáy là tam giác đều, vì vậy, tâm của đáy là giao điểm của ba trung tuyến của tam giác đều.
- Trung tuyến của tam giác đều chia nó thành hai tam giác vuông đều, và chiều dài của trung tuyến tính bằng:
\(\text{Trung tuy}\overset{ˊ}{\hat{\text{e}}}\text{n}=\frac{a \sqrt{3}}{2}=\frac{20 \sqrt{3}}{2}=10\sqrt{3}\textrm{ }\text{cm}\)Bây giờ, ta có một tam giác vuông với cạnh huyền là 20 cm (là cạnh của mặt bên tam giác đều) và một cạnh góc vuông là trung tuyến \(10 \sqrt{3}\) cm (là khoảng cách từ đỉnh đến tâm đáy).
Dùng định lý Pythagoras để tính chiều cao \(h\) của hình chóp:
\(h^{2} + \left(\right. 10 \sqrt{3} \left.\right)^{2} = 20^{2}\) \(h^{2} + 300 = 400\) \(h^{2} = 100\) \(h = 10 \textrm{ } \text{cm}\)Bước 3: Tính thể tích của hình chóp
Thể tích của hình chóp được tính theo công thức:
\(V = \frac{1}{3} \times A_{đ \overset{ˊ}{\text{a}} \text{y}} \times h\)Áp dụng giá trị của \(A_{đ \overset{ˊ}{\text{a}} \text{y}}\) và \(h\) vào công thức:
\(V = \frac{1}{3} \times 100 \sqrt{3} \times 10\) \(V = \frac{1}{3} \times 1000 \sqrt{3} = 333 , 33 \sqrt{3} \approx 577 , 35 \textrm{ } \text{cm}^{3}\)Kết luận:
Thể tích của hình chóp là khoảng 577,35 cm³.