Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ta có \(\widehat{AMB}=\widehat{AKB}=90^0\)( góc nội tiếp chắn nửa (O)
=>\(\widehat{AKB}+\widehat{BIE}=90^0+90^0=180^0\)
=> Tứ giác IEKB nội tiếp đường tròn
b)+)Ta có \(AB\perp MN\)tại \(\widebat{AM}=\widebat{AN}\)
=>\(\widehat{AME}=\widehat{AKM}\)( 2 góc nội tiếp cùng chắn 2 cung bằng nhau)
tam giác AME zà tam giác AKM có\(\widehat{MAK}\)chung
\(\widehat{AME}=\widehat{AKM}\left(cmt\right)\)
=> tam giác AME = tam giác AKM(g.g)
=>\(\frac{AM}{AK}=\frac{AE}{AM}=AM^2=AE.AK\)
+) ta có \(\widehat{AMB}=90^0\)(góc nội tiếp chắn nửa đường tròn , áp dụng hệ thức lượng trong tam giác zuông có
\(MB^2=BỊ.AB\)
Dó đó\(AE.AK+BI.AB=MA^2+MB^2=AB^2=4R^2\)(do tam giác AMB zuông tại H )
c) ..........

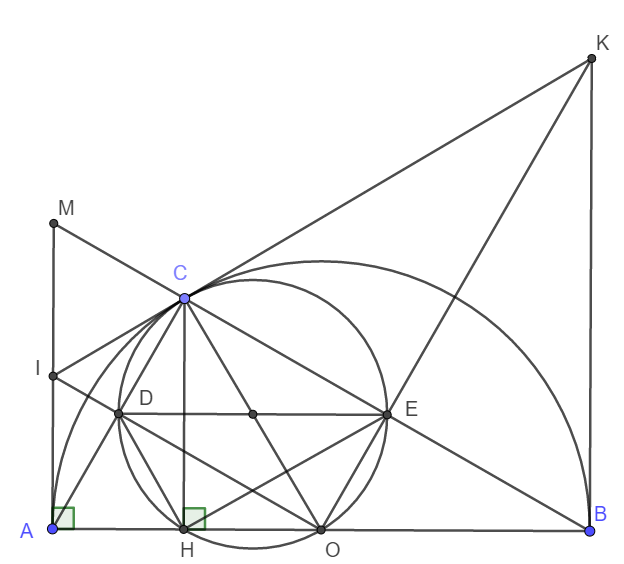
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>ΔACD vuông tại C
mà CM là đường trung tuyến
nên CM=AD/2=AM=DM
Xét ΔMAO và ΔMCO có
MA=MC
MO chung
AO=CO
DO đó: ΔMAO=ΔMCO
Suy ra: \(\widehat{MAO}=\widehat{MCO}=90^0\)
hay MC là tiếp tuyến của (O)
b: Ta có: MC=MA
nên M nằm trên đường trung trực của AC(1)
Ta có: OC=OA
nên O nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra OM là đường trung trực của AC
hay OM vuông góc với AC tại trung điểm của AC

Dưới đây là hướng dẫn giải bài toán hình học về nửa đường tròn (O) với các điểm và đoạn thẳng như đã cho:
Đề bài tóm tắt
a) Chứng minh: \(H K \bot E F\)
Phân tích và hướng giải
b) Tìm giá trị lớn nhất của \(I F^{2} + H B^{2}\)
Phân tích và hướng giải
Gợi ý giải bằng tọa độ
Nếu bạn muốn, mình có thể giúp bạn làm chi tiết từng bước với tọa độ cụ thể. Bạn có thể cho biết bạn muốn giải theo phương pháp hình học thuần túy hay sử dụng tọa độ nhé!