Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1 cm = 0,01 m
Gọi A là bản dương và B là bản âm ( Mốc ) ,
Tức VB = 0V
E = UAB / d = 120 / 0,01 = 12000 V/m
( Vì điện trường đều nên vecto E bằng nhau tại mọi điểm )
U MB = E.dMB = VM - VB ( do VB bằng 0 làm mốc )
=> VM = E.dMB = 12000.6.10^-3 = 72 V
1 cm = 0,01 m
Gọi A là bản dương và B là bản âm ( Mốc ) ,
Tức VB = 0V
E = UAB / d = 120 / 0,01 = 12000 V/m
( Vì điện trường đều nên vecto E bằng nhau tại mọi điểm )
U MB = E.dMB = VM - VB ( do VB bằng 0 làm mốc )
=> VM = E.dMB = 12000.6.10^-3 = 72 V

Đáp án B
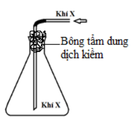
Thu bằng cách để xuôi bình nên X nặng hơn không khí nên X là NH3 hoặc Cl2. Bông tẩm dung dịch kiềm nên X là Cl2.

Đáp án B
Thu bằng cách để xuôi bình nên X nặng hơn không khí nên X là NH3 hoặc Cl2. Bông tẩm dung dịch kiềm nên X là Cl2.

Đáp án A
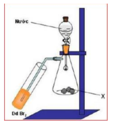
X khi tác dụng với nước tạo ra chất khí làm nhạt màu dung dịch Br2
A đúng vì khí tạo ra C2H2 làm nhạt màu dung dịch Br2
B sai do không tạo khí
C sai do không tạo khí
D tạo khí CH4 không làm nhạt màu dung dịch Br2

Áp dụng công thức A = q.UMN = -1,6.10-19.50 = -8.10-18J.

Chọn đáp án D
(a). Kim cương và than chì là hai dạng thù hình của cacbon. Chuẩn
(b). Trong phản ứng với nhôm, cacbon đóng vai trò là chất khử. Sai chất oxh
(c). Than hoạt tính được dùng trong mặt nạ phòng độc. Chuẩn
(d). Ở nhiệt độ cao, khí CO khử được CuO và Fe3O4. Chuẩn

lời giải của con là
Bước 1: Xác định các điểm và thông tin cho bài toán
Bước 2: Tính toán các tọa độ của các điểm
Giả sử hệ tọa độ 3D với gốc tại \(A\), ta có thể định nghĩa các điểm trong không gian như sau:
Vì \(M\) là trung điểm của \(C D\), nên tọa độ của \(M\) là:
\(M \left(\right. \frac{a + 0}{2} , \frac{a + 0}{2} , 0 \left.\right) = \left(\right. \frac{a}{2} , \frac{a}{2} , 0 \left.\right)\)Bước 3: Xác định mặt phẳng \(S B M\)
Để xác định phương trình của mặt phẳng \(S B M\), ta cần 3 điểm trên mặt phẳng này: \(S \left(\right. 0 , 0 , 2 a \left.\right)\), \(B \left(\right. a , 0 , 0 \left.\right)\), và \(M \left(\right. \frac{a}{2} , \frac{a}{2} , 0 \left.\right)\).
Vậy ta cần tính vector pháp tuyến của mặt phẳng \(S B M\), bằng cách lấy tích vecto của 2 vector nằm trong mặt phẳng này:
\(\overset{\rightarrow}{S B} = B - S = \left(\right. a , 0 , - 2 a \left.\right)\) \(\overset{\rightarrow}{S M} = M - S = \left(\right. \frac{a}{2} , \frac{a}{2} , - 2 a \left.\right)\)Tích vecto của hai vector này cho ta vector pháp tuyến của mặt phẳng \(S B M\).
Bước 4: Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(S B M\)
Sau khi có được phương trình mặt phẳng \(S B M\), ta sử dụng công thức tính khoảng cách từ một điểm đến mặt phẳng để tính khoảng cách từ điểm \(D \left(\right. 0 , a , 0 \left.\right)\) đến mặt phẳng \(S B M\). Công thức tính khoảng cách từ điểm \(\left(\right. x_{1} , y_{1} , z_{1} \left.\right)\) đến mặt phẳng \(A x + B y + C z + D = 0\) là:
\(d = \frac{\mid A x_{1} + B y_{1} + C z_{1} + D \mid}{\sqrt{A^{2} + B^{2} + C^{2}}}\)Bây giờ, tôi sẽ thực hiện các bước tính toán này.
Khoảng cách từ điểm \(D \left(\right. 0 , a , 0 \left.\right)\) đến mặt phẳng \(S B M\) là:
\(d = \frac{2 \mid a^{3} \mid}{3 \sqrt{a^{4}}} = \frac{2 a}{3}\)Vậy, khoảng cách từ điểm \(D\) đến mặt phẳng \(S B M\) là \(\frac{2 a}{3}\).
Mong thầy tick cho con ak
con thưa thầy đáp án của con là
a) 24%
b)94%
Mong thầy tick cho con ak