Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Vẽ đồ thị hàm số \(y = x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} = - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
- Vẽ đồ thị hàm số \(y = - x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{{ - 1}} = 3\) ta được điểm \(C\left( {3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = - x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(C\).
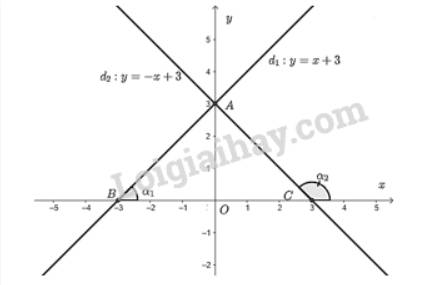
Từ đồ thị ta thấy giao điểm của hai đường thẳng là \(A\left( {0;3} \right)\).
Đường thẳng \({d_1}\) cắt trục \(Ox\) tại \(B\left( { - 3;0} \right)\).
Đường thẳng \({d_2}\) cắt trục \(Oy\) tại \(C\left( {3;0} \right)\).

a: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m+1=-\dfrac{1}{2}\\-5< >3\left(đúng\right)\end{matrix}\right.\)
=>\(m+1=-\dfrac{1}{2}\)
=>\(m=-\dfrac{3}{2}\)
b: Thay x=2 vào y=x+3, ta được:
\(y=2+3=5\)
Thay x=2 và y=5 vào (d), ta được:
\(2\left(m+1\right)-5=5\)
=>2(m+1)=10
=>m+1=5
=>m=5-1=4
c: Tọa độ A là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m+1\right)x-5=0\cdot\left(m+1\right)-5=-5\end{matrix}\right.\)
=>A(0;-5)
\(OA=\sqrt{\left(0-0\right)^2+\left(-5-0\right)^2}=\sqrt{0^2+5^2}=5\)
Tọa độ B là:
\(\left\{{}\begin{matrix}\left(m+1\right)x-5=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(m+1\right)x=5\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{m+1}\\y=0\end{matrix}\right.\)
=>\(B\left(\dfrac{5}{m+1};0\right)\)
\(OB=\sqrt{\left(\dfrac{5}{m+1}-0\right)^2+\left(0-0\right)^2}\)
\(=\sqrt{\left(\dfrac{5}{m+1}\right)^2}=\dfrac{5}{\left|m+1\right|}\)
Ox\(\perp\)Oy
=>OA\(\perp\)OB
=>ΔOAB vuông tại O
ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot5\cdot\dfrac{5}{\left|m+1\right|}=\dfrac{25}{2\left|m+1\right|}\)
Để \(S_{AOB}=5\) thì \(\dfrac{25}{2\left|m+1\right|}=5\)
=>\(2\left|m+1\right|=5\)
=>|m+1|=5/2
=>\(\left[{}\begin{matrix}m+1=\dfrac{5}{2}\\m+1=-\dfrac{5}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=-\dfrac{7}{2}\end{matrix}\right.\)

a, H là trực tâm của \(\Delta ABC\left(gt\right)\Rightarrow BH\perp AC,CH\perp AB\)
Mà \(CK\perp AC,BK\perp AB\left(gt\right)\)
\(\Rightarrow BH//CK,CH//BK\)
\(\Rightarrow BHCK\)là hình bình hành.
b, Hình bình hành BHCK có 2 đường chéo BC,HK cắt nhau tại O
\(\Rightarrow O\)là trung điểm của HK.
ON là đường trung bình của \(\Delta AHK\Rightarrow ON=\frac{1}{2}AH\Rightarrow AH=2ON\)
c, Tứ giác ABCK có: \(\widehat{BAC}+\widehat{ABK}+\widehat{ACK}+\widehat{BKC}=360^0\)
\(\Rightarrow60^0+90^0+90^0+\widehat{BKC}=360^0\Rightarrow\widehat{BKC}=150^0\)
BH//CK(gt) \(\Rightarrow\widehat{BKC}+\widehat{HCK}=180^0\)
\(\Rightarrow150^0+\widehat{HCK}=180^0\Rightarrow\widehat{HCK}=30^0\)
BHCK là hình bình hành (cmt) nên \(\hept{\begin{cases}\widehat{BHC}=\widehat{BKC}=150^0\\\widehat{HBK}=\widehat{HCK}=30^0\end{cases}}\) (tính chất hbh)

a) * Vẽ đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Cho x = 0 thì y = 3, ta được điểm P(0; 3) thuộc đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Cho y = 0 thì x = 6 ta được điểm A(6; 0) thuộc đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Vậy đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\) là đường thẳng đi qua hai điểm P(0; 3) và điểm A(6; 0).
* Vẽ đồ thị hàm số y = 2x – 2
Cho x = 0 thì y = -2 ta được điểm Q(0; -2) thuộc đồ thị hàm số y = 2x – 2
Cho y = 0 thì x = 1 ta được điểm B(1; 0) thuộc đồ thị hàm số y = 2x -2
Vậy đồ thị hàm số y = 2x – 2 là đường thẳng đi qua hai điểm Q(0; -2) và B(1; 0)
b) Ta có: A là giao điểm của đường thẳng \(y = - \dfrac{1}{2}x + 3\) với trục hoành nên \( - \dfrac{1}{2}x + 3 = 0\) suy ra x = 6 nên A(6; 0)
Ta có: B là giao điểm của đường thẳng y = 2x – 2 với trục hoành nên 2x – 2 = 0 suy ra x = 1 nên B(1; 0)
Xét phương trình hoành độ giao điểm của hai đường thẳng \(y = - \dfrac{1}{2}x + 3\) và y = 2x – 2 ta có:
\(\begin{array}{l} - \dfrac{1}{2}x + 3 = 2{\rm{x}} - 2\\ \Rightarrow 3 + 2 = \dfrac{1}{2}x + 2{\rm{x}}\\ \Rightarrow 5 = \dfrac{5}{2}x\\ \Rightarrow x = 2 \Rightarrow y = 2\end{array}\)
Vì C là hoành độ giao điểm của hai đường thẳng \(y = - \dfrac{1}{2}x + 3\) và y = 2x – 2 nên C(2; 2)
Gọi H là hình chiếu của C lên trục Ox
Khi đó: CH = 2
Mặt khác AB = 5 cm
Diện tích tam giác ABC là; \({S_{ABC}} = \dfrac{1}{2}CH.AB = \dfrac{1}{2}.2.5 = 5\left( {c{m^2}} \right)\)

a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x=1-3x\\y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=1\\y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}\\y=\dfrac{2}{5}\end{matrix}\right.\)
b: Thay x=1/5 và y=2/5 vào y=kx+1, ta được:
1/5k+1=2/5
=>1/5k=-3/5
hay k=-3

a:
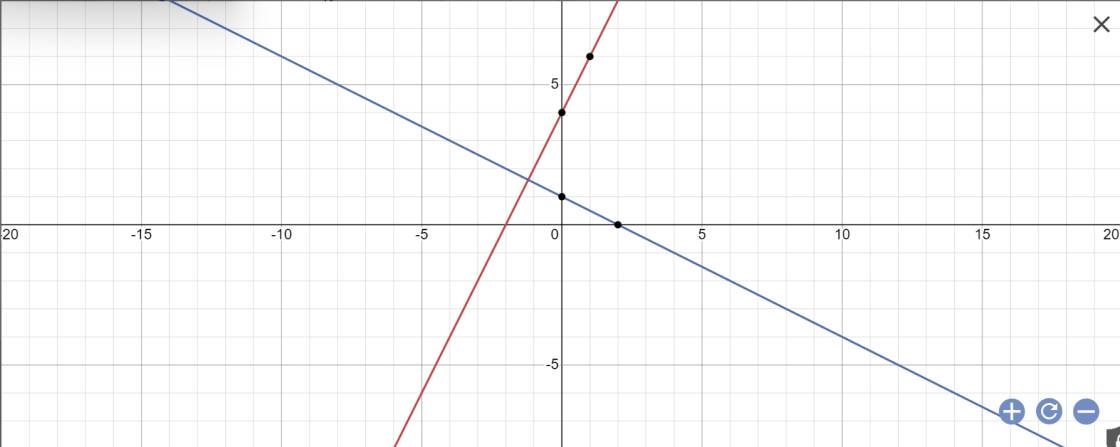
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\2x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=2x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0+4=4\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Tọa độ M là:
\(\left\{{}\begin{matrix}2x+4=-\dfrac{1}{2}x+1\\y=2x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{2}x=-3\\y=2x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3:\dfrac{5}{2}=-3\cdot\dfrac{2}{5}=-\dfrac{6}{5}\\y=2\cdot\dfrac{-6}{5}+4=\dfrac{-12}{5}+4=\dfrac{8}{5}\end{matrix}\right.\)
A(-2;0); C(2;0); M(-1,2;1,6)
\(AC=\sqrt{\left(2+2\right)^2+\left(0-0\right)^2}=\sqrt{4^2}=4\)
\(AM=\sqrt{\left(-1,2+2\right)^2+\left(1,6-0\right)^2}=\dfrac{4\sqrt{5}}{5}\)
\(CM=\sqrt{\left(-1,2-2\right)^2+1,6^2}=\dfrac{8\sqrt{5}}{5}\)
Vì \(MA^2+MC^2=AC^2\)
nên ΔMAC vuông tại M
c: Vì ΔMAC vuông tại M
nên \(S_{MAC}=\dfrac{1}{2}\cdot MA\cdot MC=\dfrac{1}{2}\cdot\dfrac{4\sqrt{5}}{5}\cdot\dfrac{8\sqrt{5}}{5}=\dfrac{2\cdot8}{5}=\dfrac{16}{5}\)

a)
* Xét đường thẳng y = x
Cho x = 1 suy ra y = 1 nên điểm (1; 1) thuộc đường thẳng y = x
Đường thẳng y = x đi qua 2 điểm O(0; 0) và (1; 1)\
* Xét đường thẳng y = -x + 2
Cho x = 2 thì y = -2 + 2 = 0 nên điểm (2; 0) thuộc đường thẳng y = - x+ 2
Cho y = 2 suy ra x = 0 nên điểm (0; 2 ) thuộc đường thẳng y = -x + 2
Đường thẳng y = - x + 2 đi qua hai điểm (2; 0) và (0; 2)
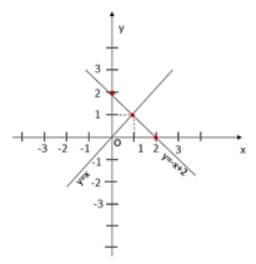
b) Giao điểm A của hai đường thẳng đã cho là A(1;1)
c) Cho y =0 ta được −x + 2 = 0 hay x = 2, suy ra B(2; 0).
Gọi C là giao điểm của đường thẳng y = −x + 2 và trục Oy. Suy ra C(0; 2). Dễ thấy tam giác OBC vuông cân tại O (vì OB = OC = 2).
Xét hai tam giác OAB và OAC có:
cạnh OA chung;
OB = OC;
\( \widehat {OBA} = \widehat {OCA} = 45^0\)
Do đó \(\Delta OAB = \Delta OAC\), từ đó suy ra AB = AC.
Điều này chứng tỏ A là trung điểm của BC, mà \(\Delta OBC \) cân tại O nên \(OA \bot AB\), tức là \(\Delta OAB\) vuông tại A.
d)
Đường thẳng y = x có hệ số góc bằng 1.
Đường thẳng y = - x + 1 có hệ số góc bằng -1
Tích của hai hệ số góc bằng -1
a: Vẽ đồ thị:
b: Tọa độ điểm C là:
\(\left\{{}\begin{matrix}-x+4=x-4\\y=-x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x=-8\\y=-x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-4+4=0\end{matrix}\right.\)
=>C(4;0)
Tọa độ A là:
\(\left\{{}\begin{matrix}x=0\\y=-x+4=-0+4=4\end{matrix}\right.\)
=>A(0;4)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x-4=0-4=-4\end{matrix}\right.\)
=>B(0;-4)
c: A(0;4); B(0;-4); C(4;0)
\(AB=\sqrt{\left(0-0\right)^2+\left(-4-4\right)^2}=8\)
\(AC=\sqrt{\left(4-0\right)^2+\left(0-4\right)^2}=4\sqrt{2}\)
\(BC=\sqrt{\left(4-0\right)^2+\left(0+4\right)^2}=4\sqrt{2}\)
Xét ΔABC có \(CA^2+CB^2=\left(4\sqrt{2}\right)^2+\left(4\sqrt{2}\right)^2=32+32=64=8^2=AB^2\)
nên ΔCAB vuông tại C
=>\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot4\sqrt{2}\cdot4\sqrt{2}=16\)
Vì xao con gà lại gáy 🤔😒