Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{21.28}{2}=294\left(cm^2\right)\)
Ta có:\(S_{ABC}=\dfrac{AB.AC}{2}\) mà ta lại có: \(S_{ABC}=\dfrac{AH.BC}{2}\)
\(\Rightarrow\dfrac{AB.AC}{2}=\dfrac{AH.BC}{2}\Rightarrow AB.AC=AH.BC\left(đpcm\right)\)

a:
BC=35cm
\(AH=\dfrac{AB\cdot AC}{BC}=16.8\left(cm\right)\)
b: \(AE=\dfrac{AH^2}{AC}=\dfrac{16.8^2}{28}=10.08\left(cm\right)\)
\(AD=\dfrac{AH^2}{AB}=\dfrac{16.8^2}{21}=13.44\left(cm\right)\)
Do đó: \(S_{AED}=\dfrac{AD\cdot AE}{2}=\dfrac{13.44\cdot10.08}{2}=67.7376\left(cm^2\right)\)

a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot21\cdot28=294\left(cm^2\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\)
mà \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\)
nên \(AH\cdot BC=AB\cdot AC\)
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=21^2+28^2=1225\)
=>\(BC=\sqrt{1225}=35\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{15}=\dfrac{DC}{20}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)
mà DB+DC=BC=35cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{35}{7}=5\)
=>\(DB=5\cdot3=15\left(cm\right);DC=4\cdot5=20\left(cm\right)\)

Xét ΔABC vuông tại A, áp dụng định lí py-ta-go ta có:
\(BC^2=AB^2+AC^2\)
\(=21^2+28^2\)
\(=1225\)
->\(BC=\sqrt{1225}=35\left(cm\right)\)
Xét ΔABC có AD là tia phân giác ta có:
\(\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AB+AC}{BC}hay\dfrac{21}{BD}=\dfrac{28}{CD}=\dfrac{21+28}{35}=\dfrac{7}{5}\)
⇒\(BD=\dfrac{21.5}{7}=15\left(cm\right)\)
⇒\(CD=\dfrac{28.5}{7}=20\left(cm\right)\)

a) Xét tam giác HBA và tam giác ABC có
góc H = góc A =900
góc B chung
=> tam giác HBA = tam giác ABC (g,g)
tam giác ABC có
góc A = 900
áp dụng định lí pytago vào tam giác vuông ABC ta có
BC2=AB2+AC2
BC2= 212+282
BC2= 441+784
BC2=1225
=>BC=35 (cm)
Vì tam giác HBA ~ tam giác ABC (cmt)
\(\frac{AH}{AC}=\frac{AB}{CB}=>AH=\frac{AB.CA}{CB}=\frac{21.28}{35}=16.8\left(cm\right)\)
chúc bn học tốt

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/AB
=>BA^2=BH*BC
b: \(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
AC=căn 16*25=20(cm)
S=15*20/2=150cm2
c: AD/DC=HA/HC=12/16=3/4
 hình vẽ
hình vẽ câu a)
câu a)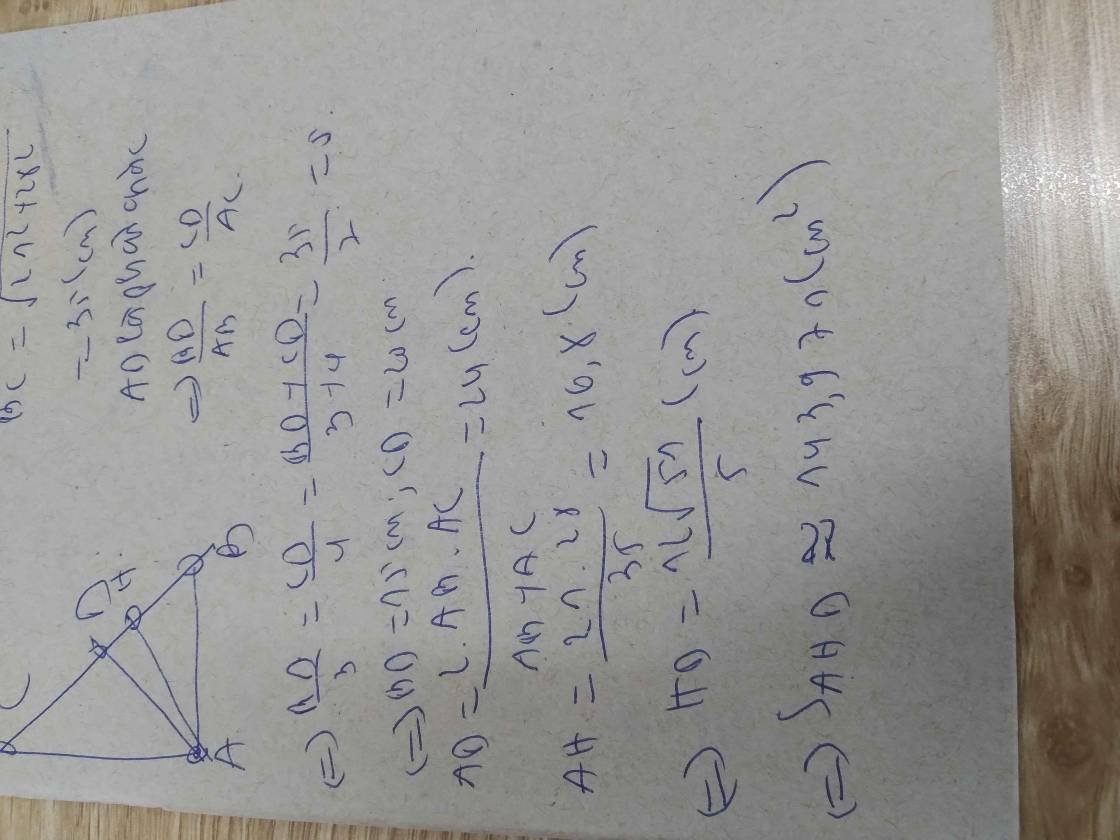
Sửa đề: HE\(\perp\)AB tại E, HD\(\perp\)AC tại D
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB=\sqrt{21^2-16,8^2}=12,6\left(cm\right)\)
Ta có: HB+HC=BC
=>HC=BC-HC=35-12,6=22,4(cm)
Xét ΔHAB vuông tại H có HE là đường cao
nên \(HE\cdot AB=HA\cdot HB\)
=>\(HE=\dfrac{HA\cdot HB}{AB}=\dfrac{12,6\cdot16,8}{21}=10,08\left(cm\right)\)
ΔAEH vuông tại E
=>\(EA^2+EH^2=AH^2\)
=>\(EA=\sqrt{AH^2-HE^2}=\sqrt{16,8^2-10,08^2}=13,44\left(cm\right)\)
Xét tứ giác AEHD có \(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\)
nên AEHD là hình chữ nhật
=>AD=HE=10,08(cm)
ΔAED vuông tại A
=>\(S_{AED}=\dfrac{1}{2}\cdot AD\cdot AE=\dfrac{1}{2}\cdot13,44\cdot10,08=67,7376\left(cm^2\right)\)
???