Question

[Thao vy]

Bài 6: Cho tam giác nhọn ABC có. Đường tròn tâm O đường kính BC cắt AB, AC lân lượt tại E và D. Hai đường thẳng BD và CE cắt nhau tại H. a) Chứng minh: tứ giác AEHD nội tiếp. b) Gọi K là trung điểm của AH. Chứng minh tứ giác OEKD nội tiếp. c) Cho BAC=60° và BC = 8 cm. Tính độ dài đoạn DE và tỉ số diện tích của hai tam giác AED và ABC.

Answer 1

[Nguyễn Lê Phước Thịnh]

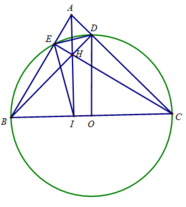
a: Xét (O) có

ΔBEC nội tiếp

BC là đường kính

Do đó: ΔBEC vuông tại E

=>CE\(\perp\)AB tại E

Xét (O) có

ΔBDC nội tiếp

BC là đường kính

Do đó: ΔBDC vuông tại D

=>BD\(\perp\)AC tại D

Xét tứ giác AEHD có \(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)

nên AEHD là tứ giác nội tiếp đường tròn đường kính AH

b: Xét ΔABC có

BD,CE là các đường cao

BD cắt CE tại H

Do đó: H là trực tâm của ΔABC

=>AH\(\perp\)BC

=>\(\widehat{ABC}+\widehat{BAH}=90^0\)

mà \(\widehat{BAH}+\widehat{EHA}=90^0\)(ΔAEH vuông tại E)

nên \(\widehat{ABC}=\widehat{AHE}\)

KE=KH

=>ΔKEH cân tại K

=>\(\widehat{KEH}=\widehat{KHE}\)

ΔOEC có OE=OC

nên ΔOEC cân tại O

=>\(\widehat{OEC}=\widehat{OCE}\)

\(\widehat{KEO}=\widehat{KEH}+\widehat{OEH}=\widehat{KHE}+\widehat{OCE}\)

\(=\widehat{EBC}+\widehat{ECB}=90^0\)

AEHD nội tiếp đường tròn đường kính AH

=>AEHD nội tiếp (K)

=>KE=KH=KD=KA

Xét ΔKEO và ΔKDO có

KE=KD

OE=OD

KO chung

Do đó: ΔKEO=ΔKDO

=>\(\widehat{KEO}=\widehat{KDO}=90^0\)

=>OEKD là tứ giác nội tiếp

c: Xét ΔADB vuông tại D có \(cosBAD=\dfrac{AD}{AB}\)

=>\(\dfrac{AD}{AB}=cos60=\dfrac{1}{2}\)

Xét ΔADB vuông tại D và ΔAEC vuông tại E có

\(\widehat{DAB}\) chung

Do đó: ΔADB~ΔAEC

=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)

=>\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)

Xét ΔADE và ΔABC có

\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)

\(\widehat{DAE}\) chung

Do đó: ΔADE~ΔABC

=>\(\dfrac{DE}{BC}=\dfrac{AD}{AB}=\dfrac{1}{2}\)

=>\(DE=\dfrac{BC}{2}=\dfrac{8}{2}=4\left(cm\right)\)

ΔADE~ΔABC

=>\(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)

Answer 2

[Hán Quang An]

Câu a: Chứng minh tứ giác AEHD nội tiếp

Ta cần chứng minh:
Tứ giác \(A E H D\) nội tiếp ⇔ 4 điểm A, E, H, D cùng nằm trên một đường tròn

Cách làm:

• Gọi \(\left(\right. O \left.\right)\) là đường tròn đường kính \(B C\)
• Vì \(D , E\) nằm trên đường tròn đường kính \(B C\) ⇒
  \(\angle E = \angle E B C\) là góc nội tiếp chắn nửa đường tròn, nên:
  \(\angle E=90^{\circ}(\text{t}ươ\text{ng t}ự\text{ };\angle D=90^{\circ})\)
• \(\angle E H D\) là góc giữa hai đường cao từ \(E\) và \(D\), tức cũng là góc vuông

⇒ \(\angle E H D = 90^{\circ}\), và \(\angle E A D = 90^{\circ}\)

Vậy:

\(\angle EHD+\angle EAD=180^{\circ}\Rightarrow AEHD\text{ n}ộ\text{i ti}\overset{ˊ}{\hat{\text{e}}}\text{p}\)

✅ Kết luận: \(A E H D\) là tứ giác nội tiếp.

---

Câu b: Gọi K là trung điểm của AH. Chứng minh tứ giác OEKD nội tiếp

Phân tích:

• Tứ giác \(O E K D\) nội tiếp ⇔ tổng hai góc đối nhau bằng 180°, hoặc có 4 điểm cùng nằm trên một đường tròn.
• Ta đã có:
• • \(\angle E = \angle E B C = 90^{\circ}\)
  • \(\angle D = \angle D C B = 90^{\circ}\)

=> Hai điểm \(E\) và \(D\) nằm trên đường tròn đường kính BC

• \(O\) là trung điểm đoạn \(B C\) ⇒ tâm đường tròn.
• Điểm \(K\) là trung điểm đoạn \(A H\), mà \(H\) là giao điểm \(B D\) và \(C E\) (hai đường chéo của tứ giác \(A E H D\))

Để chứng minh \(O E K D\) nội tiếp, một cách hiệu quả là chứng minh góc đối bằng nhau hoặc tổng bằng \(180^{\circ}\).

Nhưng ta thử góc vuông:

• Ta biết \(\angle O D E = \angle O E D = 90^{\circ}\) vì \(O D ⊥ A C\), \(O E ⊥ A B\)

Và trung điểm \(K\) của \(A H\) cũng có vị trí "đối xứng" trong tứ giác \(A E H D\), nên thường sẽ thỏa mãn tính chất nội tiếp với \(O , D , E\)

📌 Ta dùng định lý tứ giác nội tiếp: 4 điểm cùng thuộc một đường tròn nếu và chỉ nếu:

\(\angle O K D + \angle O E D = 180^{\circ}\)

Lúc này có thể dựng các tam giác vuông và chứng minh các góc đó phụ nhau.

✅ Vì điều này hơi dài dòng nếu không có hình vẽ cụ thể, bạn cứ nhớ rằng:
Tứ giác OEKD nội tiếp là hệ quả từ cấu trúc đặc biệt của hình vẽ, sử dụng các góc vuông ở \(D\) và \(E\), trung điểm \(K\) và đường tròn tâm \(O\).